CV mach 3

[JohnNichols]

[JohnNichols]

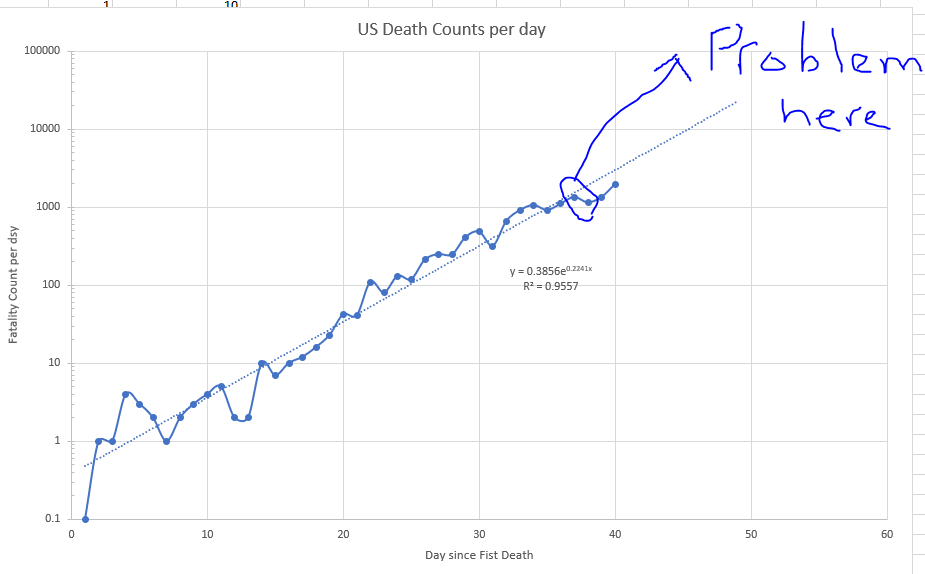
We lost 2 days - but it is back on track -- losing 2 days may not be a peak

[JohnNichols]

[JohnNichols]

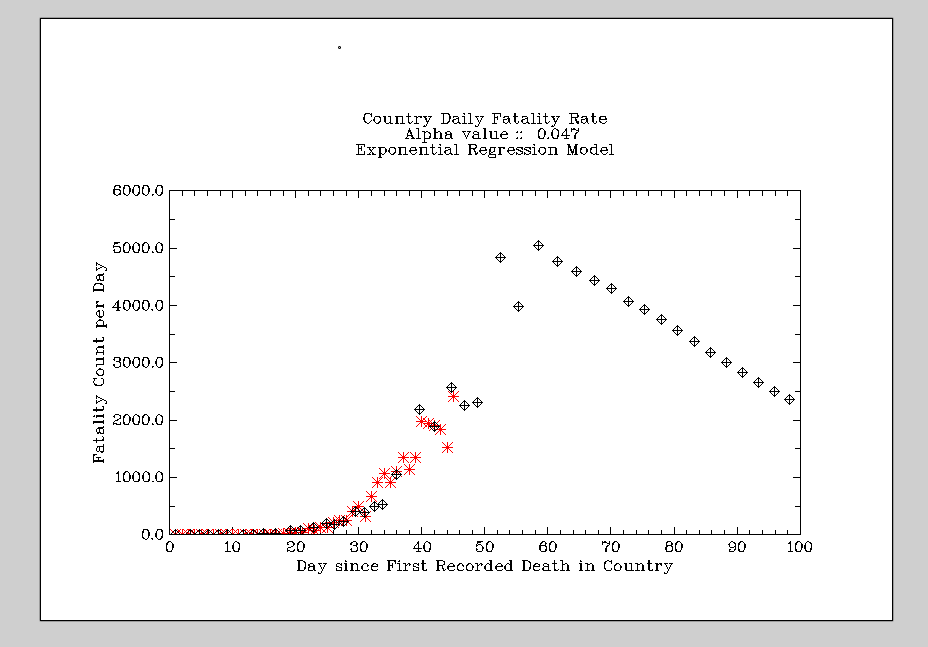
The Chines ODE matches well so far,  the HIME model says this is close to the peak -- at 2200  -- this model is really close to standard data for Wuhan except for the rate to quarantine -- which is half the Wuhan rate.  

The harmonic is due to a Weiner process on one of the varaible, at 0.5% level -- this thing is really sensitive - 

[JohnNichols]

Can I rewind a file if i just opened it?  

[andrew_4619]

Nichols, John wrote:

Can I rewind a file if i just opened it?  

Yes

[JohnNichols]

[JohnNichols]

This is the Fortran ODE Solver coupled with CONREC -- the Fortran CONREC was written by Paul Bourke from Australia.  He published the original code in BYTE.

I translated the Fortran into C# for modelling FFT results from an accelerometer.   

This shows the plot of the ODE solutions for time along the X axis -- 512 days 

and the alpha value for the ODE's from 0.1 to 0.01 on the Y axis. 

The z values are scaled by taking the fourth root otherwise you end up with only a few contours because of the huge differential - taking the log is a problem for the zeros.  

John

[JohnNichols]

[JohnNichols]

   SUBROUTINE derivs(x,y,dydx)
    implicit none
    INTEGER nrhs
    REAL x,y(*),dydx(*), alpha, pop, Beta,NBeta, lambda, kappa, delta, gamma, randdata, rho
    COMMON nrhs
    common /RAND/ randdata(1000000), alpha,Beta,gamma, lambda, kappa, delta, rho
    nrhs=nrhs+1

    ! if(nrhs .lt. 32) then

    ! else
    ! rho = 0.5
    ! end if
    pop = 1.0
    Beta = 1.0                      !  Infection Rate
    NBeta = Beta/pop
    gamma = 0.5                     ! latency time 2 days
    lambda = 0.015                  ! cure rate  Wuhan 0.1 to 0.2 - time based
    kappa = 0.01                  ! mortality rate
    delta = 1.0/7.4                 ! quarantine time 7.4 days

    lambda = lambda * ((0.005*randdata(nrhs)) + 0.995)
    write(*,1000)nrhs,lambda,alpha
1000 format(i4,2('   ', F6.4))
    !  y(1) is susceptible
    !  y(2) is exposed
    !  y(3) is infected
    !  y(4) is quarantined
    !  y(5) is recovered
    !  y(6) is Death
    !  y(7) is Insusceptible

    dydx(1) = -rho*NBeta*y(1)*y(3) - alpha*y(1)                        ! Equation 1
    !dydx(1) = -NBeta*y(1)*y(3) - alpha*y(1)                           ! Equation 1
    dydx(2) = (rho*Nbeta*y(1)*y(3)) - gamma*y(2)                       ! Equation 2
    !dydx(2) = (Nbeta*y(1)*y(3)) - gamma*y(2)                          ! Equation 2
    dydx(3) = gamma*y(2) - delta*y(3)                                  ! Equation 3
    dydx(4) = delta*y(3) - lambda*y(4) - kappa*y(4)                    ! Equation 4
    dydx(5) = lambda*y(4)                                              ! Equation 5
    dydx(6) = kappa* y(4)                                              ! Equation 6 - correct
    dydx(7) = alpha*y(1)                                               ! Equation 7

    ! write(*,120) nrhs, dydx(1),dydx(2),dydx(3),dydx(4),dydx(5),dydx(6),dydx(7)
120 Format(1x,i4, 7(2x,f14.6))

    return
    END

The original model matches well upto 40th day, but the stuff after does not make great sense,  the idea is to introduce RHO into the equations, but this poor match and now we have a 900 death jump in one day -- RHO will never predict this properly -- one idea is that RHO has a dependence on something else - say temperature.  

Can I ask each of you to give me some idea if your area got a lot colder in the last 24 hours - the death increase was not spotty it was across the board. 

This virus is a beast. 

Any ideas on fixing the model  -- I have tried other models but they all end up with the same overall shape. 

JMN

[JohnNichols]

[JohnNichols]

If I play with lambda with the random offset -- the above is 0.1% random variation in lambda -- results in the above graph. 

Why do you think we get a cluster around 40 days in real data and model?  Aside from the 0.1 this has been constant since about day 28. 

it is weird,

[Hevia__Orlando]

Nichols, John wrote:

   SUBROUTINE derivs(x,y,dydx)
    implicit none
    INTEGER nrhs
    REAL x,y(*),dydx(*), alpha, pop, Beta,NBeta, lambda, kappa, delta, gamma, randdata, rho
    COMMON nrhs
    common /RAND/ randdata(1000000), alpha,Beta,gamma, lambda, kappa, delta, rho
    nrhs=nrhs+1

    ! if(nrhs .lt. 32) then

    ! else
    ! rho = 0.5
    ! end if
    pop = 1.0
    Beta = 1.0                      !  Infection Rate
    NBeta = Beta/pop
    gamma = 0.5                     ! latency time 2 days
    lambda = 0.015                  ! cure rate  Wuhan 0.1 to 0.2 - time based
    kappa = 0.01                  ! mortality rate
    delta = 1.0/7.4                 ! quarantine time 7.4 days

    lambda = lambda * ((0.005*randdata(nrhs)) + 0.995)
    write(*,1000)nrhs,lambda,alpha
1000 format(i4,2('   ', F6.4))
    !  y(1) is susceptible
    !  y(2) is exposed
    !  y(3) is infected
    !  y(4) is quarantined
    !  y(5) is recovered
    !  y(6) is Death
    !  y(7) is Insusceptible

    dydx(1) = -rho*NBeta*y(1)*y(3) - alpha*y(1)                        ! Equation 1
    !dydx(1) = -NBeta*y(1)*y(3) - alpha*y(1)                           ! Equation 1
    dydx(2) = (rho*Nbeta*y(1)*y(3)) - gamma*y(2)                       ! Equation 2
    !dydx(2) = (Nbeta*y(1)*y(3)) - gamma*y(2)                          ! Equation 2
    dydx(3) = gamma*y(2) - delta*y(3)                                  ! Equation 3
    dydx(4) = delta*y(3) - lambda*y(4) - kappa*y(4)                    ! Equation 4
    dydx(5) = lambda*y(4)                                              ! Equation 5
    dydx(6) = kappa* y(4)                                              ! Equation 6 - correct
    dydx(7) = alpha*y(1)                                               ! Equation 7

    ! write(*,120) nrhs, dydx(1),dydx(2),dydx(3),dydx(4),dydx(5),dydx(6),dydx(7)
120 Format(1x,i4, 7(2x,f14.6))

    return
    END

The original model matches well upto 40th day, but the stuff after does not make great sense,  the idea is to introduce RHO into the equations, but this poor match and now we have a 900 death jump in one day -- RHO will never predict this properly -- one idea is that RHO has a dependence on something else - say temperature.  

Can I ask each of you to give me some idea if your area got a lot colder in the last 24 hours - the death increase was not spotty it was across the board. 

This virus is a beast. 

Any ideas on fixing the model  -- I have tried other models but they all end up with the same overall shape. 

JMN

Is it possible you share the rest of the code?

In any case, thank you by the equations and values of parameters.

OPH.

[JohnNichols]

Here is the complete code, you will need to add DISLIN -- not hard to find and download. 

The code comes from Peng - see paper -- the Chinese gov has shut down all communication so contacting them is not recommended for their safety

The Feng module has been amended from her published algorithm as her code did not work -- I amended equation 1 -- do not use it -- until it is properly fixed 

The alpha from the Chinese is 0.1  -- this is impossible a standard alpha is 0.5  refer to Brauer

[JohnNichols]

One plausible explanation for these population increases is that the bubonic
plague invasions served to control the population size, and when this control
was removed the population size increased rapidly.

----------------------------------------------------------------------------------------------------------------

Cheery thought for the day as to why Fortran was invented -- bubonic plague went away 

[JohnNichols]

In developing countries it is quite common to have high birth rates and
high disease death rates. In fact, when disease death rates are reduced by
improvements in health care and sanitation it is common for birth rates to
decline as well, as families no longer need to have as many children to ensure
that enough children survive to take care of the older generations. Again, it
is plausible to assume that population size would grow exponentially in the
absence of disease but is controlled by disease mortality.

----------------------------------------------------------------------------------------------------------------

Who said to read this book to improve my Fortran models -- ok a Russian 

[Hevia__Orlando]

Nichols, John wrote:

Here is the complete code, you will need to add DISLIN -- not hard to find and download. 

The code comes from Peng - see paper -- the Chinese gov has shut down all communication so contacting them is not recommended for their safety

The Feng module has been amended from her published algorithm as her code did not work -- I amended equation 1 -- do not use it -- until it is properly fixed 

The alpha from the Chinese is 0.1  -- this is impossible a standard alpha is 0.5  refer to Brauer

Thank you very much!

I am user of DISLIN since the 90's, a great package.

[JohnNichols]

[JohnNichols]

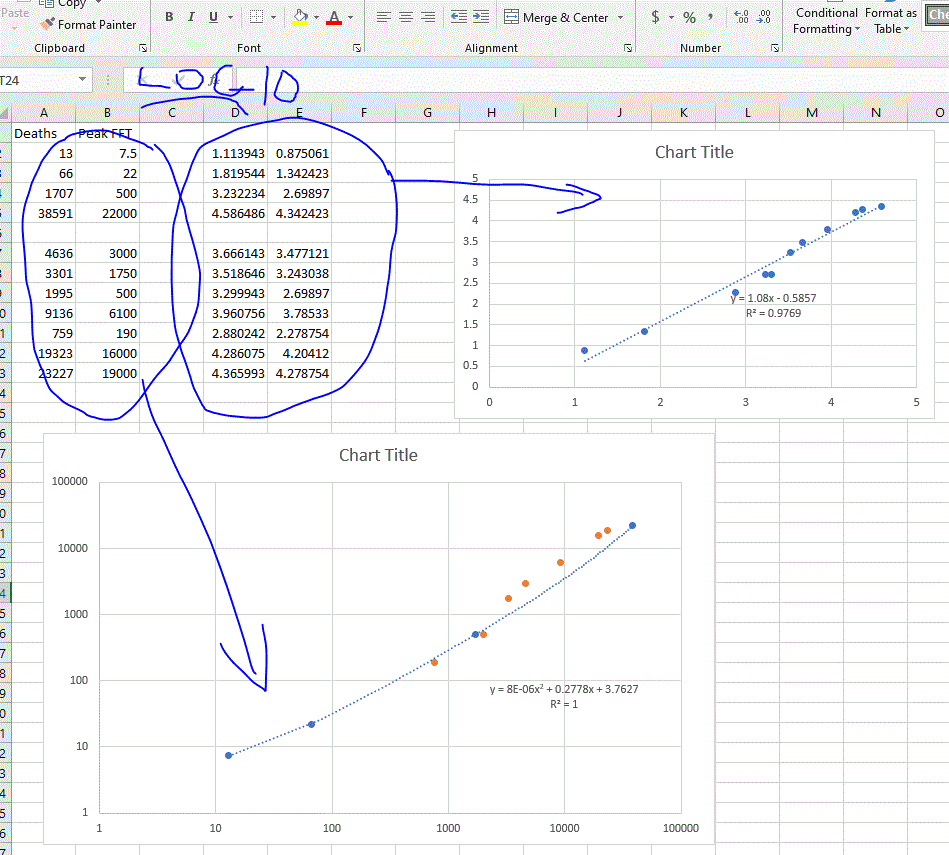
The last picture shows the relationship between the deaths and the peak FFT for Australia, China, UK Germany and France and USA

This is the residuals for the linear regression 

Darn that is a tight fit 

[JohnNichols]

On the bottom graph the four blue ones are Australia and USA for 28th March and 19th April

[JohnNichols]

it is 4pm GMT, there are only 1/3 of the US states reporting and you are at 1100 deaths -- there are huge increases on the east coast outside NY -- it is a terrible day by the looks.

if you are wondering what happened to the Fortran analysis - here is the draft paper 

I would appreciate any comments --