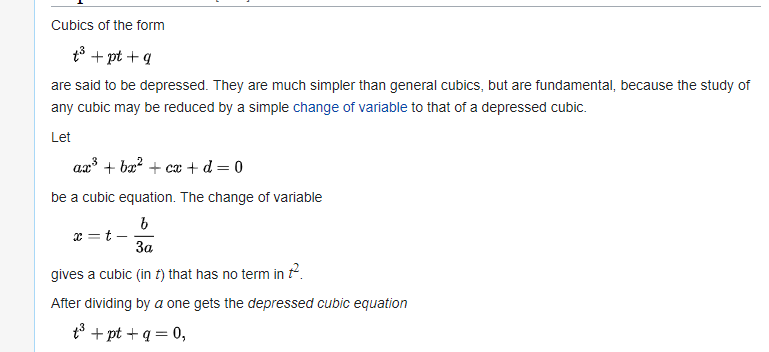- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
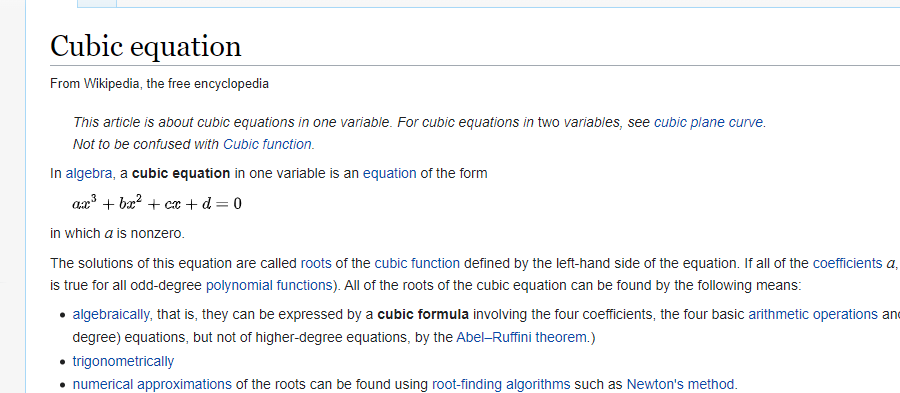
https://en.wikipedia.org/wiki/Cubic_equation
a can be set to one with division.
if a == 1 than q == 1, we may then get around problem of p being integer, only testing will tell.
The heart of the method developed by Cardano and others.
Then:
and the solution:
... as presented elsewhere.
The Cardano and other solutions rely on some interesting and smart observations, essentially involving depressed cubics.
So -- if you start with real a,b,c,d only, you cannot solve these equations in Fortran without using complex numbers. I tried and you run into NAN, you change to complex and you get the correct answers for some classes of a,b,c,d, but the current Fortran code does not work for a,b,d > 0 and C < 0.
Hence my interest in signum, because of one of the alternative solutions shown on Fortran discourse and to program that set of equations in Fortran requires complex signum or the equations are wrong.
Hence defining complex signnum allowing for all of the variations is a trivial exercise in logic.
signum(z) for z = a+bi
if a and b > 0 then z = 1+1i
if a and b < 0 z = -1-1i
if a >0 and b < 0 then z = 1 -1i
if a < 0 and b > 0 then z = -1+1i
the set (1,1), (1,-1) (-1,-1) and (-1,1) for the four quadrants of the complex plane. and the zero of course can have equivalent equations.
I was playing with the code. I was not trying for production quality and I was using the equation outlines in Fortran discourse, I did not check them.
It is just fun, of course there are limits, but I am not writing for 12 yr olds, so I leave out the limits.
John
Link Copied
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page