- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The McMaster programmer using the CDC 6400 and Fortran IV continues to use this type of statement
IF(EA(I) .eq. 0.0) GO TO 7124In the thesis, he complains that sometimes it does not converge, so he added a second coarse routine, I have not got to yet. This is causing the main convergence problem at the moment, I can fix it, but I wonder how many old programs had this problem. This is not the first of these in the code.
In 1972 would a civil engineering masters student have understood the problem with the above if statement, I know in 1977 Conte and deBoore certainly would not have done this. How much was Fortran being taught in the late 1960s and early 1970s?
Why would he think that EA would ever return a zero, and how close would it have to get to trip the if, at the moment I have a 10 to the -69 and it does not trip it.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jim:
I have the McMaster program looping and I am starting to understand their underlying method.
I enclose the sln folder and the only sample in the thesis.
The program loops adding P delta effects to an elastic analysis of a concrete column looking for the cracking, essentially.
IF(NCYCL .LE. 1) GOTO 9573 ! Changed from 1 to 0
KADD2 = 0
KADD = 0
DO 7379 I= 1,NPLAST
IF(NCYCL .GE. GO TO 5127
GOTO 8128
5127 RATIO1 = (EIII(NCYCL,I)-EIII(NCYCL-1,I) ) /EIII(NCYCL,I)
GOTO 8129
8128 RATIO1=(EI(I)-EEI(I))/EI(I)
8129 RATIO2=(EAAA(NCYCL,I)-EAAA(NCYCL-1,I)/EAAA(NCYCL,I))
RATIOI=ABS(RATIO1)
RATIOA=ABS(RATIO2)
IF(NCYCL.GT.5) GOTO 7009
IF(RATIOI .LE. 0.01 .AND. RATIOA .LE. 0.01) KADD2 = KADD2 + 1
IF(NCYCL .LE. 5) GOTO 7008
7009 IF(NCYCL.GT.10) GO TO 7007
IF(RATIOI .LE.0.02 .AND. RATIOA .LE. 0.02) KADD2=KADD2+1
IF(NCYCL.LE.10) GOTO 7008
7007 IF(NCYCL.GT.15) GO TO 7006
IF(RATIOI .LE.0.04 .AND. RATIOA .LE. 0.04) KADD2=KADD2+1
IF(NCYCL .LE. 15) GOTO 7008
7006 IF(NCYCL .GT. 20) GOTO 7008
IF(RATIOI .LE. 0.10 .AND. RATIOA .LE. 0.10) KADD2=KADD2 + 1
7008 CONTINUE
count = count + 1
write(15,200)count,NCYCL,I,RatioI,RatioA,KADD2,EIII(NCYCL,I),EIII(NCYCL-1,I),EAAA(NCYCL,I),EAAA(NCYCL-1,I)
200 Format(I10,",",I10,",",I10,",",F10.3,",",F10.3,",",I10,4(",",E15.7))
7379 CONTINUE
He uses ratioa and ratioI to determine if the solution has converged, but EIII, EAAA, the Young's Modulus times the Inertia and the Area respectively slowly converge towards zero. It is a slow change as he gets closer to the true delta and the estimated strains. But his equations take two small quantities EIII and EAAA and subtract the last increment and then divide by the first, so the ratios go all over the place. There is an a.xls which shows the graphed values from the print statement at Line 26.
The idea has merit, the equations need to be checked etc... But have you got a thought on the convergence criteria, thanks, I was thinking of a simple sum of the differences and seek a low number.
JMN
The results seem to show a crack at the second lowest element, which makes sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
IF(NCYCL .LE. 1) GOTO 9573 ! Changed from 1 to 0
KADD2 = 0
KADD = 0
IF(NCYCL.LE.5) THEN
RATIOX = 0.01
ELSEIF(NCYCL.LE.10) THEN
RATIOX = 0.02
ELSEIF(NCYCL.LE.15) THEN
RATIOX = 0.04
ELSEIF(NCYCL .LE. 20) THEN
RATIOX = 0.10
ELSE
STOP "You figure out what to do"
ENDIF
DO I= 1,NPLAST
IF(NCYCL == 1) THEN
RATIO1=(EI(I)-EEI(I))/EI(I)
ELSE
RATIO1 = (EIII(NCYCL,I)-EIII(NCYCL-1,I) ) /EIII(NCYCL,I)
ENDIF
RATIO2=(EAAA(NCYCL,I)-EAAA(NCYCL-1,I)/EAAA(NCYCL,I))
RATIOI=ABS(RATIO1)
RATIOA=ABS(RATIO2)
IF(RATIOI .LE. RATIOX .AND. RATIOA .LE. RATIOX) KADD2 = KADD2 + 1
count = count + 1
write(15,200)count,NCYCL,I,RatioI,RatioA,KADD2,EIII(NCYCL,I),EIII(NCYCL-1,I),EAAA(NCYCL,I),EAAA(NCYCL-1,I)
200 Format(I10,",",I10,",",I10,",",F10.3,",",F10.3,",",I10,4(",",E15.7))
END DOThe above doesn't appear to perform a conversion. Instead it is performing a frequency count.
Haven't looked at Hebe yet.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jim:
This code is not worth characters used to type it.
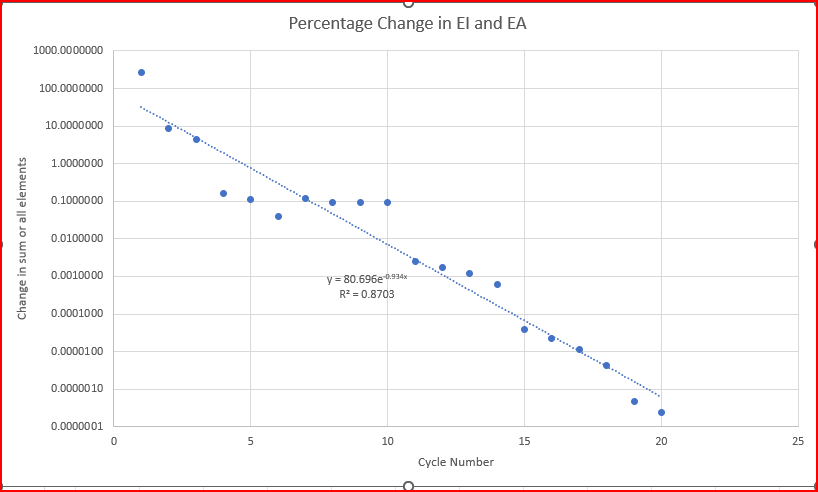
I went back to basics and looked at the output data for the EI and the EA. With some plotting one can arrive at a graph that looks at the % value of sum(EI + EA) against the original values and get a nice graph.
What he is doing now makes sense, he finds the elastic solution and computes the P delta from solution 1, then solves for P delta and gets new delta, delta approaches zero, very fast as seen above.
it is then a matter of deciding what level of change is acceptable, after 20 iterations we are at a change in the 10th sign figure, at that stage we should accept the answer.
Now I can code it.
Just explaining it here, forces me to think about. I will drop the new Hebe on shortly then we can look at the real stuff. The zip files shows the xls file with all the graphs. The interesting element is the fourth element, it is clearly the cracking point.
Thanks
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
John,
I can give you some pointers as to what is happening and where to look. The nity-gritty part I will leave up to you.
The joint displacements converge at iteration 12 (13, 14 are same, didn't look further)
However, the revised EA and EI appear to oscelate (not to same values but some sort of up and down).
Rearranging your report and clipping out unnecessary information we see:
Joint Displacement X Displacement Y Rotation XY
in in radians
1 -0.012000 0.000000 -0.000317
1 -0.006915 0.000000 -0.000307
1 -0.005631 0.000000 -0.000302
1 -0.005510 0.000000 -0.000301
1 -0.005430 0.000000 -0.000300
1 -0.005394 0.000000 -0.000300
1 -0.005386 0.000000 -0.000300
1 -0.005380 0.000000 -0.000300
1 -0.005376 0.000000 -0.000300
1 -0.005373 0.000000 -0.000300
1 -0.005372 0.000000 -0.000300
1 -0.005372 0.000000 -0.000300
1 -0.005372 0.000000 -0.000300
2 -0.009600 -0.006095 -0.000190
2 -0.005545 -0.005899 -0.000184
2 -0.004525 -0.005791 -0.000181
2 -0.004435 -0.005774 -0.000180
2 -0.004375 -0.005761 -0.000180
2 -0.004347 -0.005758 -0.000180
2 -0.004340 -0.005754 -0.000179
2 -0.004335 -0.005751 -0.000179
2 -0.004332 -0.005750 -0.000179
2 -0.004330 -0.005748 -0.000179
2 -0.004329 -0.005747 -0.000179
2 -0.004329 -0.005747 -0.000179
2 -0.004329 -0.005746 -0.000179
3 -0.007200 -0.009142 -0.000063
3 -0.004168 -0.008849 -0.000061
3 -0.003391 -0.008688 -0.000061
3 -0.003312 -0.008666 -0.000061
3 -0.003259 -0.008649 -0.000061
3 -0.003237 -0.008645 -0.000061
3 -0.003231 -0.008639 -0.000061
3 -0.003226 -0.008635 -0.000061
3 -0.003223 -0.008633 -0.000061
3 -0.003221 -0.008630 -0.000061
3 -0.003221 -0.008630 -0.000061
3 -0.003221 -0.008629 -0.000061
3 -0.003221 -0.008629 -0.000061
4 -0.004800 -0.009142 0.000063
4 -0.002768 -0.008848 0.000062
4 -0.002255 -0.008693 0.000060
4 -0.002208 -0.008676 0.000060
4 -0.002176 -0.008663 0.000060
4 -0.002162 -0.008660 0.000060
4 -0.002158 -0.008655 0.000060
4 -0.002155 -0.008651 0.000060
4 -0.002153 -0.008649 0.000060
4 -0.002152 -0.008646 0.000060
4 -0.002151 -0.008646 0.000060
4 -0.002151 -0.008646 0.000060
4 -0.002151 -0.008645 0.000060
1 5 -0.002400 -0.006095 0.000190
2 5 -0.001370 -0.005898 0.000184
3 5 -0.001121 -0.005796 0.000181
4 5 -0.001106 -0.005787 0.000181
5 5 -0.001095 -0.005780 0.000180
6 5 -0.001088 -0.005778 0.000180
7 5 -0.001086 -0.005775 0.000180
8 5 -0.001085 -0.005772 0.000180
9 5 -0.001084 -0.005771 0.000180
10 5 -0.001084 -0.005769 0.000180
11 5 -0.001084 -0.005769 0.000180
12 5 -0.001084 -0.005769 0.000180
13 5 -0.001084 -0.005768 0.000180
6 0.000000 0.000000 0.000317
6 0.000000 0.000000 0.000307
6 0.000000 0.000000 0.000302
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
6 0.000000 0.000000 0.000301
Member Concrete Concrete Axial Applied Revised Revised Curvature LOOPS
Number Comp Tensile Force Moment EI EA A B
Strain Strain kips in-kip (> 5000 not convg.)
11 1 0.002 0.001 0.001 0.120 0.602E+03 0.164E+01 0.200E-03 64 7
12 1 0.002 0.001 0.000 0.121 0.603E+03 0.593E+00 0.200E-03 12 7
13 1 0.011 0.001 0.000 0.004 0.178E+02 0.166E+00 0.200E-03 259 0
2 0.002 0.001 0.000 0.002 0.750E+01 0.500E+00 0.200E-03 2 47
2 0.002 0.001 0.000 0.000 0.773E+00 0.237E+00 0.200E-03 422 0
2 0.002 0.001 0.000 0.000 0.320E+00 0.173E+00 0.200E-03 125 0
3 0.002 0.001 0.001 0.004 0.213E+02 0.161E+01 0.200E-03 2 88
3 0.002 0.001 0.001 0.001 0.619E+01 0.156E+01 0.200E-03 564 0
3 0.002 0.001 0.000 0.001 0.327E+01 0.662E+00 0.200E-03 9 122
4 0.011 0.001 0.001 0.001 0.633E+01 0.597E+00 0.200E-03 0 0
4 0.002 0.001 0.001 0.001 0.347E+01 0.112E+01 0.200E-03 26 0
4 0.002 0.001 0.000 0.000 0.625E+00 0.190E+00 0.200E-03 275 0
5 0.002 0.001 0.001 0.001 0.610E+01 0.113E+01 0.200E-03 9 232
5 0.002 0.001 0.000 0.001 0.328E+01 0.902E+00 0.200E-03 49 0
5 0.011 0.001 0.000 0.000 0.443E+00 0.582E-01 0.200E-03 0 0
Two likely candidates (there may be more)
a) you have converged, but your convergence detection is in error
b) the EA and/or EI are feeding back 0.0 for displacement adjustments
What I suggest you do is to run the debugger, and on say step 2, locate in the code where the EI/EA feed back non-zero displacements. Then, place break there, and then continue each iteration observing how you convert the EI/EA values into displacements X/Y/Z. Then when on the break where the displacements are 0.0. You should be able to determine if you actually converged .OR. the code generating the displacements is subject to values benieth the roundoff error position. Note, this does not mean that the correct displacement is insignificant, but rather the algorithm used is sensitive (faulty) with respect to precision.
FWIW on a project I am working on now, it is doing deployment of a very long tether (on the order of 500,000,000 feet) with integration step size very small 0.1E-8 it ramps up later). Using double precision numbers, and acceleration of 1ft/s/s, the initial amount of tether deployed goes in the bit bucked. IOW no deployment is calculated. The resolution was to hold shadowing variables as REAL(16) to accumulate the displacements, then copy them back into the REAL(8). IOW parodically the REAL(8) used throughout the program gets updated to the correct value within the precision of the REAL(8).
As to if this is the root of your problem (bad algorithm), I cannot say, but I can say that using REAL(16) intermediaries is a quick way to assess the situation (and may direct you to a better solution using the REAL(8)'s).
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jim:
I had to chuckle, this is why this forum is so good, in my life I have met, five people with that sort of skill shown in your last post, the first was a red headed boy in Physics 1, he aced the class, first class nerd, the second is my structures lecturer Peter Kleeman, a long way into being best structural engineer ever, who just quietly sat and taught, you, @mecej4 and Steve, and there is the urban myth about the guy at the IBM lab, who the management consultants were told to leave out of the review report. I remember reading the story and laughing.
I worked out the convergence, and your comments are great, I was wondering about the blip.
Now I can look at creep. The next stage.
How do I specify a REAL(16)? in the
INTEGER, PARAMETER :: dp = selected_real_kind(15, 307)
method? No idea.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
INTEGER, PARAMETER :: qp = selected_real_kind(30) ! will do, assuming compiler supports quad precision (ifort and ifx do)
Someone (mecj4 or Fortran Fan) posted something like this
EDIT OOPS
integer, parameter :: sp = selected_real_kind(precision(0.0))
integer, parameter :: dp = selected_real_kind(precision(0.0_sp) * 2)
integer, parameter :: qp = selected_real_kind(precision(0.0_dp) * 2)
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I suppose that works, but it makes me a bit uncomfortable as it's sort of a cheat. My preference would be to see the actual number of decimal digits required, but I understand if all you really want is "quad precision".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
How do I not cheat? In other words what is the correct method?
It is not relevant with Hebe as Pardiso even in the latest iteration at the purchased level is real(8).
There is a double convergence, the first convergence is for the elastic to plastic and the second for creep, which is a minor change.
SUBROUTINE STAT(Code,I,J,EI,EA, SUM, oldsum)
use base
Implicit none
Integer, INTENT(IN) :: Code,I,J
integer K
REAL (KIND=dp), INTENT(IN) :: EI(mn_20,mn_30)
REAL (KIND=dp), INTENT(IN) :: EA(mn_20,mn_30)
REAL (KIND=dp), INTENT(INOUT) :: SUM
REAL (KIND=dp), INTENT(INOUT) :: OLDSUM
OLDSUM = SUM
if(code == 0) then
sum = ZERO
end if
do 10 k=1,j
sum = sum + EI(I,k)+EA(I,K)
10 end do
write(*,20)I,J,sum,oldsum,abs(sum-oldsum),deltaS
20 Format(//,20X," Cycle :: ",I10,&
/,20X," Plastic elements :: ",I10,&
/,20X," Convergence number :: ",F11.2,&
/,20X," Old Convergence number :: ",F11.2,&
/,20X," Convergence nun dufference :: ",F11.2,&
/,20X," Convergence Limit :: ",F11.2,/)
return
end subroutine stat
Here is the double convergence for when it converges on a number not zero, this is the original people's weird counting method, this is a lot simpler.
The question now is whether the equations are correct in the thesis and then the code.
Thanks
I am not sure I want to do a tethered object, no matter what loads you estimate they will be wrong. We always underestimate loads as we are using history.
JMN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
7126 CALL MPHI(PAX1,BMCL,WW1,PHI1,WEEP,WU1,NM1,UUF1,WTN,KONT,T1,T2, KI, KF,DEBUG) ! CHANGED WW1 o Wp1
IF(NM1 .GT. 0) GOTO 9111
IF(PAX1 .EQ. 0.0) GOTO 7119
IF(T1 .GT. 0.0) GO TO 7177
WTRIAL = (BMCL*DCGC)/EI(I)
PHITRI = WTRIAL / DCGC
GOTO 7076
7177 WTRIAL=WWP1(I)
PHITRI=PPHIP(I)
IF(NM2 .GT. 0.0) GO TO 7117
7076 CALL MPHI(ZERO,BMCL,WP1,PHIP1,CEEP,WU2,NM2,UUF2,W9,KONT,T1,T2, KI,KF,DEBUG)
IF(NM2.GT. 0.0) GO TO 7117
DNAX3 = WP1/PHIP1
DNAX1 = WW1/PHI1 The MPHI is a Newton Ralphson technique to get the strain distribution, when it is done at about cycle 6, PHI1 disappears to a very small number, sensing DNAX1 to 1000, when the whole thing is only 10 inches on side, so DNAX1 should not be 1000 and it then sends the waxial estimate up a lot, which affects EA. D is all the depths of section numbers, DB, DTH etc. No idea what NAX stands for.
I have found out why the thesis does not bear results, the sketched problem does not solve as shown, he had put the axial load and moment at -270 both so I changed axial load to -20 when checking. The printout shown in the listing cannot give the results he presents in the thesis as the published data is not output.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
FWIW additional thing to look out for. In the code I am working on now (tension/strain distributions along a very long tether with movable object) a computational issue arises when using (dp) sqrt to calculate a unit vector when the values are significantly less than 1.0. IOW any small variation is magnified. Keep this in mind when results are not as expected.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Estimating strains in concrete is dubious at best, but HEBE did show where the plastic hinge is most likely to occur. I spent part of last night translating the program and data into metric. Much easier to understand the answers, kips and in-kips are a pain. Now to check all the assumptions and the equations and compare it to modern theory.
I can see the problem of the short lengths, the errors in the length can affect the answer.
What happens if the tether breaks, a plane flies into it or the earthquake destroys the base?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
>>What happens if the tether breaks, a plane flies into it or the earthquake destroys the base?
A break is likely to be loss of tether, though there is some speculation that it could be recaptured and reused (I haven't seen simulations of this, so I am not convinced). The part that falls to earth won't hurt anyone if it fell on your head (similar to being hit by a falling piece of paper), the main issues are: a) it is conductive and power lines might not appreciate a short, b) entanglement should it fall over a highway or railway.
Other than sabotage, an airplane shouldn't fly into it (restricted airspace).
The base station (at least the first one) will likely be positioned ~600 miles west of the Galapagos Island on a floating platform. Unless you are flying from Lima Peru to Hawaii or Tokyo there likely won't be much air traffic. If the break occurred due to sabotage, what comes down will fall in the water. Severance by an asteroid (or sabotage by satellite) could have tether material fall across northern South America (mostly unpopulated), and mid-sothern Africa (also mostly unpopulated). IOW it would lay across the equator.
There is very little (very infrequent) bad weather conditions there, and any tsunami would have an extremely long wavelength (i.e. a few inches high). Unless told, you wouldn't know that one passed you by.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I am enjoying this discussion as I know exactly what sort of tether you're talking about. I've read many SF stories about "space elevators" and what can go wrong with them.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
IMHO, I have learnt the hard way, that if you can imagine a failure it will fail that way. Case in point, truck wash down bay, large Euclid dump trucks, tyres taller than a tall man, firehose pressures and flows from 8 nozzles, I put in 25 turn to close values to avoid water hammer. Superintendent substituted quarter to turn to close and then turned all at the same time as a test, weakest part of the system, pump casing, one large piece was found 1 kilometre away in the metal shop. I was blamed until I pointed out the stupidity of a non-approved design change.
How often do yu write Fortran programs correctly the first time, setting aside the few people on this site.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page