Roza Kotlyar is a Principal Engineer in the Quantum Computing Group at the Components Research Division of Intel Corporation and worked with Intel Labs researchers on this joint work.
Highlights:
- The 68th Annual IEEE International Electron Devices Meeting will run from December 3-7, 2022, as an in-person conference with additional on-demand content.
- Components Research and Intel Labs researchers detail our paper “Mitigating Impact of Defects on Performance with Classical Device Engineering of Scaled Si/SiGe Qubit Arrays.”
- Our work models an impact on quantum-buried Si/SiGe channel devices from low defect densities in dielectrics and semiconductor/dielectric interfaces, noting limitations from spurious dot formations on noise and fidelity and proposing potential engineering schemes for mitigating the impact of defects on quantum performance.
We are excited to detail our latest quantum computing research at the 68th Annual IEEE International Electron Devices Meeting (IEDM). The conference will run from December 3-7, 2022, as an in-person conference with additional on-demand content. A prominent event for technological innovations, IEDM features research in semiconductor and electronic device technology, design, manufacturing, physics, and modeling. We will discuss our accepted paper, “Mitigating Impact of Defects on Performance with Classical Device Engineering of Scaled Si/SiGe Qubit Arrays.”
Our work models an impact on quantum-buried Silicon (Si) channel devices embedded into Silicon Germanium (SiGe) heterostructure from low (~ 1e11 cm-2) defect densities in dielectrics and on semiconductor/dielectric interfaces. We also note a limitation that spurious dot formation sets on qubit gate operation as well as the impact of defects on voltage-dependent noise and two-qubit (2Q) gate fidelity. Finally, we show that classical device engineering schemes via scaling pitch, dielectric thickness, deeper SiGe buffers, and screening gates allow us to mitigate the impact of defects on quantum performance.
Moving Toward Practical Quantum Computing
Practical quantum computing requires millions of qubits to do computations and correct for decoherence errors. However, existing quantum systems only include tens of entangled qubits, which limits them from solving real-world problems. Si quantum dot-based technology is a natural venue for scaling that takes full advantage of advanced semiconductor process manufacturing. In addition to the scaling challenge, another significant barrier to quantum practicality is the issue of qubit fragility. Our research efforts address limitations on quantum device performance stemming from top semiconductor/dielectric surface defects with theory and simulation and discuss schemes for their mitigation.
Simulating Qubit Behavior
Design, engineering, and fabrication of physical systems for quantum computation is a mind-boggling complex problem that draws from various disciplines and requires innovations at every step. Similarly, as for our classical logic, modeling has been an indispensable tool to guide those innovations. Modeling a quantum computer on a classical computer is especially challenging due to an exponentially large number of physical states that need to be included in the models. Truly, one needs a quantum computer to simulate a quantum computer. Quantum computation simulation requires multi-physics modeling methods: from process, thermal and magnetic design to materials physics, low-temperature many-electron interactions, and quantum algorithms. A simulation helps us test ideas from a physical design concept to expected quantum performance before we build quantum computer hardware.
Electron spin up/down states provide a natural two-state system, a basic unit of quantum information called a qubit. We have developed a simulation framework at Components Research/Intel Labs to model devices from process to quantum performance. We simulate process models of structures and do a device simulation to calculate potential and electron wavefunctions. We do Object Oriented MicroMagnetic Framework (OOMMF) simulations to get magnetic field information for driving simulations. We use data from device simulations and experiments to simulate the performance of our qubit systems. Device simulation is done self-consistently with quantum correction. We have developed a Hamiltonian model simulator for qubit system performance that allows us to calculate both stationary and transient characteristics. Through these simulations, we can address the challenge of qubit fragility and offer mitigating solutions.
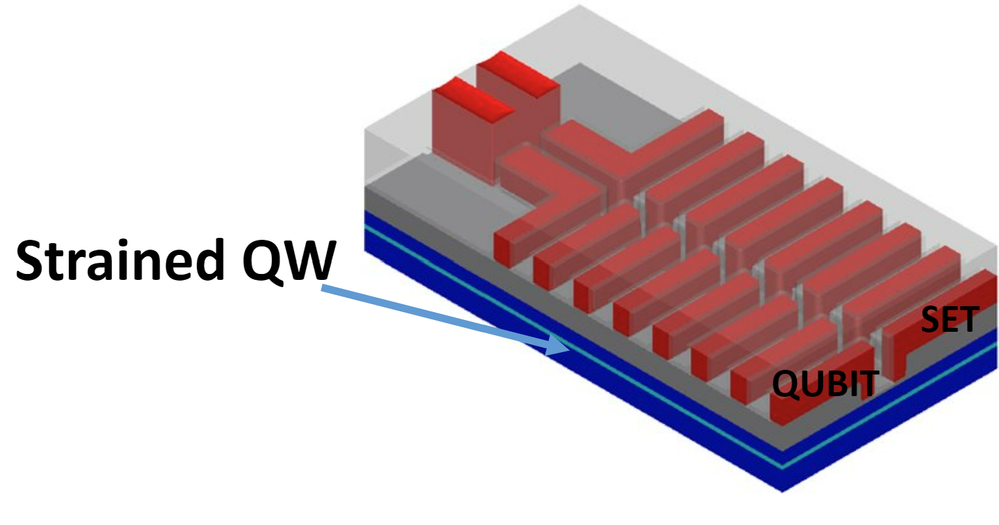
First, we form a quantum electron channel in a strained Si well embedded in a relaxed SiGe heterostructure. This confines electrons vertically. Then, we deposit dielectric on top, create holes in it from one layer to another, called vias, and fill them with metals. A qubit via serves to define quantum dots and a symmetric SET via is used as a charge sensor.
Figure 1. A schematic of our device with a QUBIT via used to define quantum dots and a symmetric SET via used as a charge sensor.
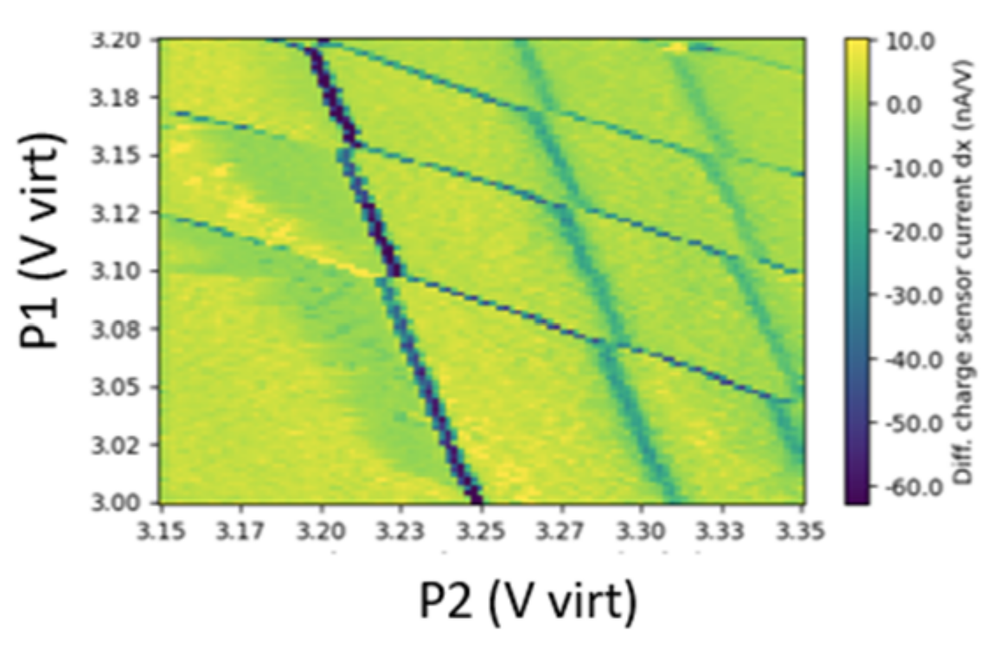
We use barriers and plungers to isolate the quantum dots laterally. Then, by varying the plunger voltages, we deplete those dots to the last electron. When states that differ by only 1 electron degenerate, the current can flow through the dot, resulting in charge addition lines. When two dots are formed under P1, and P2 plungers, the voltage of the P1 dot transition depends on the voltage of the P2 dot, as shown in Figure 2 below. The electrostatic crosstalk determines the slopes of the addition lines.
Figure 2. A clean stability diagram measured in charge sensing experiments.
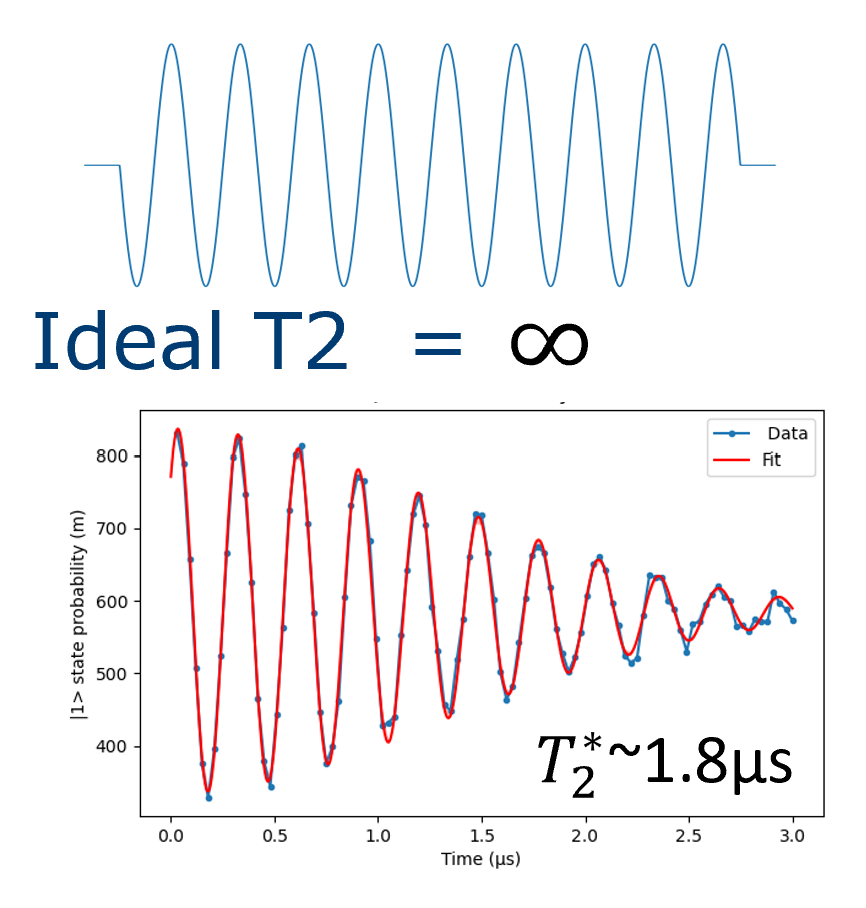
Single gate operations are accomplished through spin rotations using spin resonance driven by the electric field. We apply alternating voltage (AC) signals to barrier gates, which cause electron displacement of a dot, coupling to magnetic field gradients from the magnet placed on top to create alternating magnetic fields which drive our qubits. With no noise, ideal rotations between 0 and 1 states are expected. In our experiments, these rotations slowly decay on a scale of microsecond dephasing T2 times, as shown in Figure 3. This decay is due to noise present in our physical systems.
Figure 3. Ideal qubit state oscillations as a function of time duration when AC magnetic field is applied are expected with no noise (top figure); these oscillations, as measured, show a decay on a scale of T2 time (bottom figure).
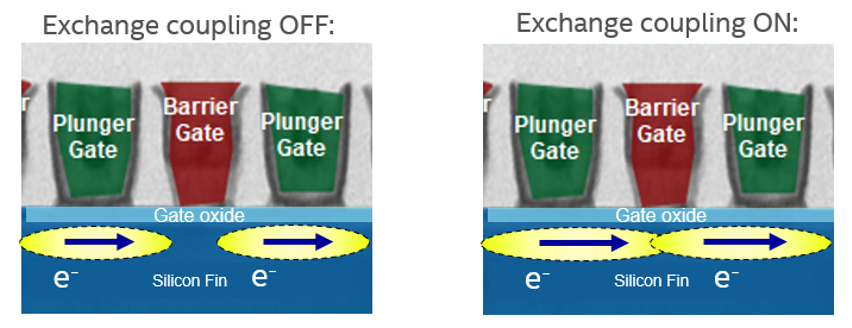
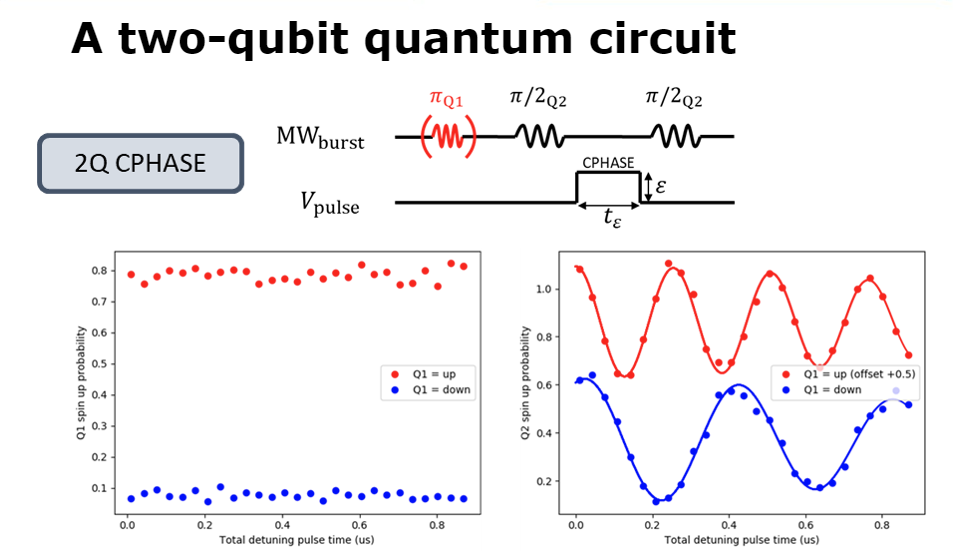
We accomplish two-gate operations by entangling electron spin through electron exchange modulation in which we pulse middle barrier voltage or detune plunger voltages between two dots (Figure 4). In the experiment illustrated by Figure 5, a 2Q Cphase gate is obtained. Series of operations on qubits are usually described with quantum circuits. Each line lists all operations on qubits. During 2Q Cphase we applied Pi/2 rotation on qubit Q2, entangled both control Q1 and target Q2 through detuning plunger voltages for both qubits, and applied the final Pi/2 rotation on Q2. As a function of detuning pulse time, the state of qubit 2 changes the oscillation phase depending on the state of control qubit 1. We can construct all operations needed for universal quantum computing from these device manipulations.
Figure 4. A schematic for 2Q gate operation on two qubits. In this operation, electron spin states are entangled (electrons are shared) by lowering the barrier separating the two qubits by either pulsing the middle gate barrier voltage or detuning the plunger voltages of two dots.
Figure 5. An experimentally realized 2Q CPHASE gate on two control Q1 and target Q2 qubits with a series of operations described in the quantum circuit (top) and a shown probability of finding these qubits in state 1 (spin up) as a function of detuning exchange pulse time for two initial states of Q1 (spin up – red, spin down – blue).
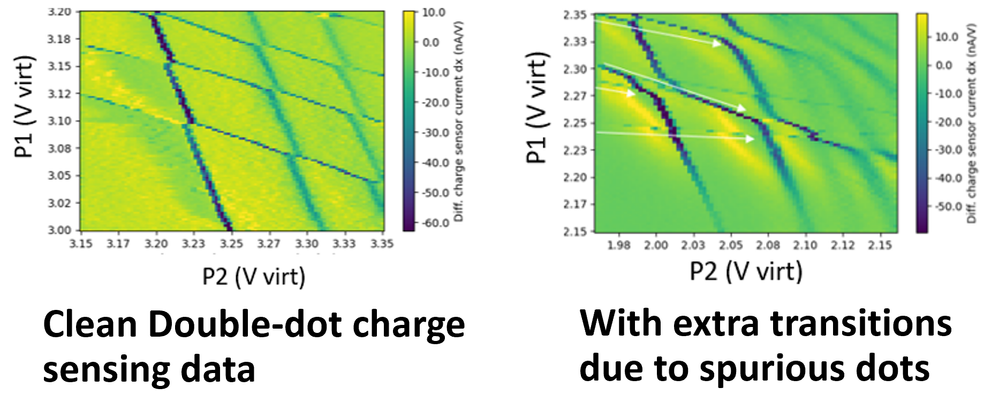
Recently, we have demonstrated a significant improvement in materials quality in buried Si quantum well devices. We obtain consistently high low-temperature Hall mobilities of ~ 200K cm2/Vs low defect densities (DIT) at ~ 1e11 cm-2 level in > 60% devices on a 300 nm wafer. This results in clean stability diagrams, as shown in Figure 6a. However, in about 30% of devices, we get extra transitions due to the formation of dots in unintended random defect-caused locations, which we call spurious dots. These extra transitions result in different slopes on stability diagrams, as indicated by the white arrows in Figure 6b.
Figure 6. (a) A clean stability diagram measured in charge sensing experiments. (b) A stability diagram with spurious transitions indicated with arrows.
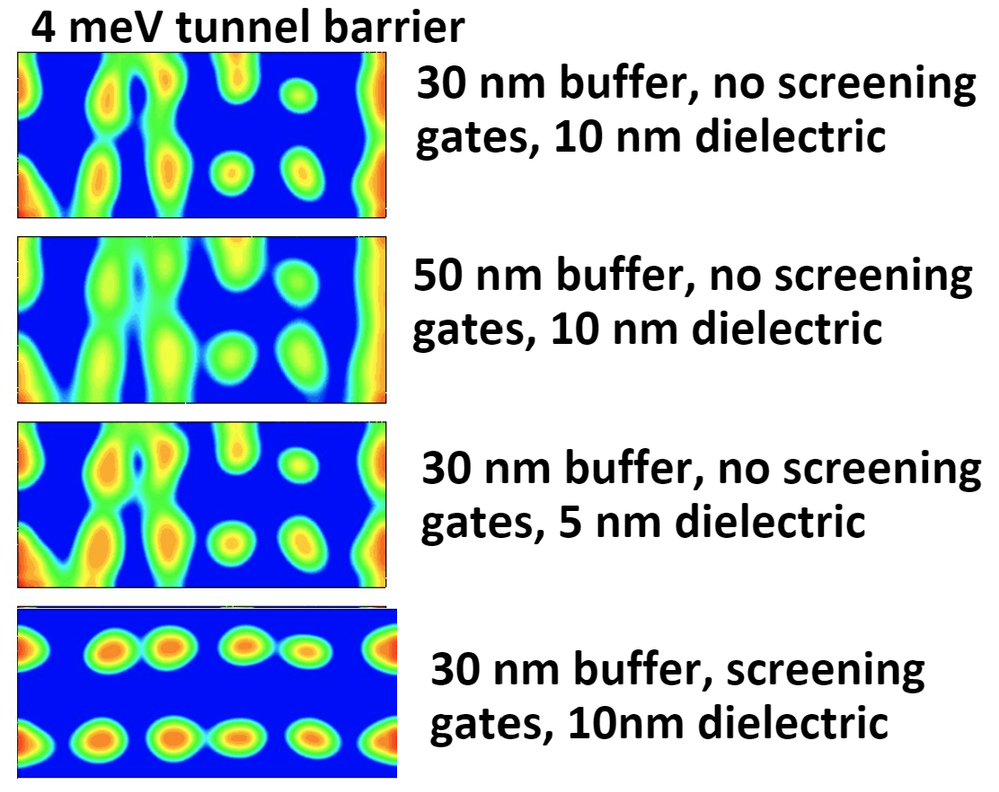
Potential perturbation due to single defects at low defect density sets the voltage/energy scales when spurious dots form (Figure 7). We assume charge defects are from vacancies in oxide or at the semi/oxide surface. We tuned four dots on the Qubit side and four dots on the SET side and placed a vacancy under the P1 plunger. A single defect causes a potential perturbation in the semiconductor, which decays with a distance from the defect, as shown in these horizontal slices from A0 to A2 taken in the middle of the well via at various depths from the interface. A quantum dot in a 50 nm buffer sees about two times smaller potential perturbation than a 30 nm dot. This potential fluctuation reduces with a thinner dielectric from a 16 nm dotted line to a 5 nm dashed line, as shown in Figure 7.
Figure 7. A single oxygen vacancy is placed in the simulation under P1, and potential perturbation caused by this defect in the semiconductor is plotted.
Defects impact device performance through charge noise. To evaluate this, we construct gate operations by replaying the experimental dot tuning with our Hamiltonian simulator. Our model uses quantum dot bandstructure, including spin and valley states, interdot tunneling, onsite and inter-site Coulomb energies, and orbital and Zeeman magnetic field effects. We define the double dot by matching the stability diagram in the data and go to virtual voltage space to define the operating range along the detuning axis.
Mitigating Defects in Quantum Devices
Upon identifying and learning about quantum defects, the next step was to determine how to mitigate the impact of those defects. We found that device engineering accomplished this. To demonstrate, first, we show electron density at a similar P1-P2 Tb barrier of ~ 4 meV for the same defect realization as in a 30 nm SiGe buffer 10 nm dielectric device. Figure 6 shows that spurious electron density defect-driven localization is reduced with a 50 nm buffer, a simulated 5 nm dielectric, and screening gates.
Figure 8. Electron density in the middle of a quantum well with eight dots tuned in the 30 nm top SiGe buffer 10 nm dielectric device with random defects present shows a reduction of spurious electron localization by going to 50 nm buffer, using thinner 5 nm dielectric and using screening gates.
The other way is to operate at interdot barriers, which are higher than spurious dot potential perturbation and achieved at scaled pitches. We expect that removing spurious dots will reduce bias-dependent noise. Additionally, defect mitigation using classical device engineering schemes could enable scaled qubit arrays within a high-volume manufacturing environment. While large-scale implementation of quantum computing may still be a somewhat distant goal, the potential benefits are vast. We aim to move closer to quantum practicality with our continued research efforts.
 Roza received the Ph.D. in theoretical condensed matter physics from the University of Maryland, College Park, in 1998. Her thesis research was on coherently coupled quantum dot arrays. Roza was awarded in 1998 a two-year National Research Council Post-Doctoral Fellowship at the Naval Research Laboratory in Washington, DC, where she focused on the research of excitonic transitions in quantum wells, quantum wires and quantum dots. In 2000 Roza joined a Device Modeling Group at TCAD at Intel Corporation, Hillsboro, OR, as a Sr. CAD Engineer and later as a Staff Research Scientist. Roza played a key role in development of major transistor technologies to enable Complementary Metal Oxide Semiconductor (CMOS) scaling: stress, metal gate, and tri-gates. These innovations were the key drivers fueling the continuation of Moore’s law to achieve high computer power at low cost. Roza has worked on modeling of Intel quantum devices since the beginning of Quantum Computing program at Intel in 2016, and in 2020 Roza joined the Quantum Hardware group full time. Roza is the author of 55+ papers in industry-leading journals, she has 40+ patents. Roza led the industry-academia collaborations through her mentoring of Semiconductor Research Corporation (SRC), and she is a recipient of 2018 Mahboob Khan Outstanding Industry Liaison SRC Award. She served on the IEEE Brunetti Award committee, and on IRPS 2019-2020 Neuromorphic Committee, on the IEEE International Electron Devices Meeting (IEDM) modeling committee, and was an organizer of special sessions at IEEE Nano 2021. Roza is a Chair of Technical committee on Modeling and Simulation (TC-10) of IEEE Nanotechnology Council. She is a Senior IEEE member. Roza is a passionate advocate for science outreach initiatives and is participating in the US Q12 education partnership. Roza brought her device modeling experience at Intel and her quantum background to model Intel spin qubit devices, starting from bandstructure description, to effective continuum modeling of devices, to many-body physics. Roza is the author of Intel quantum performance simulator which is used to understand Intel experiments and is put on the bottom of Intel SDK to run quantum algorithms.
Roza received the Ph.D. in theoretical condensed matter physics from the University of Maryland, College Park, in 1998. Her thesis research was on coherently coupled quantum dot arrays. Roza was awarded in 1998 a two-year National Research Council Post-Doctoral Fellowship at the Naval Research Laboratory in Washington, DC, where she focused on the research of excitonic transitions in quantum wells, quantum wires and quantum dots. In 2000 Roza joined a Device Modeling Group at TCAD at Intel Corporation, Hillsboro, OR, as a Sr. CAD Engineer and later as a Staff Research Scientist. Roza played a key role in development of major transistor technologies to enable Complementary Metal Oxide Semiconductor (CMOS) scaling: stress, metal gate, and tri-gates. These innovations were the key drivers fueling the continuation of Moore’s law to achieve high computer power at low cost. Roza has worked on modeling of Intel quantum devices since the beginning of Quantum Computing program at Intel in 2016, and in 2020 Roza joined the Quantum Hardware group full time. Roza is the author of 55+ papers in industry-leading journals, she has 40+ patents. Roza led the industry-academia collaborations through her mentoring of Semiconductor Research Corporation (SRC), and she is a recipient of 2018 Mahboob Khan Outstanding Industry Liaison SRC Award. She served on the IEEE Brunetti Award committee, and on IRPS 2019-2020 Neuromorphic Committee, on the IEEE International Electron Devices Meeting (IEDM) modeling committee, and was an organizer of special sessions at IEEE Nano 2021. Roza is a Chair of Technical committee on Modeling and Simulation (TC-10) of IEEE Nanotechnology Council. She is a Senior IEEE member. Roza is a passionate advocate for science outreach initiatives and is participating in the US Q12 education partnership. Roza brought her device modeling experience at Intel and her quantum background to model Intel spin qubit devices, starting from bandstructure description, to effective continuum modeling of devices, to many-body physics. Roza is the author of Intel quantum performance simulator which is used to understand Intel experiments and is put on the bottom of Intel SDK to run quantum algorithms.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.