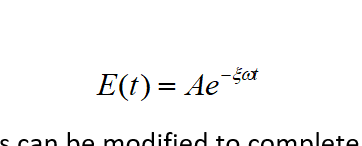- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
When compile my program I found a problem that the ifort 2021.1 compiler will interprete this immediate number 0.002362E12 as 0x41E1992860000000 in double precision float number. However the same immediate number compile use gfortran will be interprete as 41E1992840000000. This difference later accumulated to a very large difference in my program.
The test case can be abstract to following:
program test
DOUBLE PRECISION :: test1
101 FORMAT(A, Z16.16)
test1 = 0.002362E12
print 101, 'test1=', test1
end program test
compile with and execute with "ifort -O0 -fp-model precise test-imm.F90 -o test-imm.o && ./test-imm.o" will give a result "test1=41E1992860000000"
compile with and execute with "gfortran -O0 test-imm.F90 -o test-imm.o && ./test-imm.o" will give a result "test1=41E1992840000000"
Any idea why this is?
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Your test program looks innocent enough, but the literal number you specify is in fact single-precision and is interpreted by BOTH compilers as single-precision (*). It is then converted to double precision on assignment and apparently the conversion is slightly different in Intel Fortran than in gfortran.
If you change "test1 = 0.002362E12" to test1 = 0.002362D12" (or use a kind suffix - _kind-number, which is the preferred way), then the results are identical. The "D" in there (or the appropriate suffix) causes the literal number to be double precision.
(*) This is a rather fundamental property of Fortran: the right-hand side is interpreted independent of the left-hand side. This makes the semantics much simpler.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the reply.
I also found the same behavior. I konw how to avoid this kind of issue. Acctually in my original program, test1 variable is also a single precision number, which by the way also has the similar issue. The case is like following:
program test
real(4) :: test1
101 FORMAT(A, Z8.8)
test1 = 0.002362E12
print 101, 'test1=', test1
end program test
If we compile with "ifort test.F90 -O3 -fp-model precise -o test.o && ./test.o", the result is 4F0CC943.
Compile and run with gfortran test.F90 -O3 -o test.o will result in 4F0CC942.
The only way to avoid this issue is to promote the literal number to double preicison by changing the source code or using compiler option -r8, which is not make sence for user who just want to use single precision.
My question is more of a curious about why the interpretation of single precision number is different from gfortran. I did some research about the source code of gfortran, where I found that the token "0.002362E12" is transfered to single float by strtof function. But it seems ifort do not use the same way to do the transformation. Do you have any idea on why ifort behave like this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
When a real number is converted from a decimal representation to an internal binary representation (or in the opposite direction) there is potential for precision loss. Your decimal representation has only 4 decimal digits in the mantissa, which corresponds to roughly 13 bits. That leaves 23-13 = 10 bits undefined, and the value loaded into the processor depends on the method used.
The Fortran standard does not require that a processor follow any specific algorithm or use a function (such as C's strtof) to perform this task. In the language of the standard, the behavior is "implementation dependent". If you want more precision, provide more digits in the input number.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
Thanks for the reply.
Sure, I agree with you that different compiler might have different implementation on the conversion. But as I said, my question is just I am curious about how does ifort iplement this part. I also just tryed to insert an rounding mode change to upward before calling the strtof in gfortran source, which will give the same result as ifort. But it seems not likely for ifort to do such tedious conversion. Did it really insert an upward rounding before strtof? or just becuse it use it own strtof which might have a difference implementation than libc? Or maybe some other case? This part is what I am really curious about.
Any ideas?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Why the fixation on strtof()? There is no reason why any compiler use should any specific piece of software, such as that function. There is no reason why a Fortran compiler should or should not call a C routine to perform a conversion. The 80x87 section of a modern x64 CPU can do these conversions in microcode/hardware, without having to call any software routines.
Intel Fortran is not open source, and I know better than to ask for details of the internal workings of a proprietary compiler.
The two 32-bit IEEE numbers Z'4F0CC943' and Z'4F0CC942' are equidistant from your decimal number 2.362E9 by the amount ±128.0. Both are valid approximations. Ifort picks one, Gfortran picks the other. The decimal number 2.362E9 cannot be represented exactly as a 32-bit IEEE floating point number.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I cannot fully agree with you that "both are valid approximations". IEEE754 default tie break rule is round half to even. So in this case only rounding to Z'4F0CC942' confirms to IEEE754. It explains why gfortan and even ifort 19.0.0 uses Z'4F0CC942'. ifort 21.0.0's Z'4F0CC943' does not seems to be correct to me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
This interested me. It has to do with the compiler's choice for IEEE rounding modes. Intel Fortran uses the mode Fortran calls COMPATIBLE - when the value to be rounded is exactly halfway between two representable values, it picks the one "away from zero". gfortran is picking the one closer to zero, which could be similar to NEAREST, but it's allowed to go up or down.
As @mecej4 says, both values are reasonable. I would add the comment that you need to be very careful about using the correct kind value with real constants, if your application is as sensitive as you say. Also, when using large values, use of double precision is a must when you don't want to lose significance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
A somewhat agree that rounding to both are reasonable. But lack of consistency is problematic. Here is an example that inconsistent rounding approaches in different compilers end up with non-intuitive result:
$ cat sub.c
float from_c(void)
{
return 0.002362E12;
}
$ cat main.f90
program test
implicit none
interface
REAL(4) function from_c() bind(c)
end function
end interface
REAL(4) :: test1, test2
101 FORMAT(A, z8.8)
test1 = 0.002362E12
print 101, 'from_f=0X', test1
print *, test1
test2 = from_c()
print 101, 'from_c=0X', test2
print *, test2
end program test
$ ifort -O2 main.f90 -o main.o -c
$ icc -O2 -c -o sub.o sub.c
$ ifort main.o sub.o -o c
$ ./c
from_f=0X4F0CC943
2.3620001E+09
from_c=0X4F0CC942
2.3619999E+09
BTW, ifort 21.0.0 is the only compiler that differs to many others (gfortran, icc, gcc, clang, flang, ifort 19.0.0). Does it still sound reasonable?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There is an additional twist to note.
A few years ago, I learned that the floating point arithmetic model used at compile time need not be the same as the model used at run time. As a result of this, a compiler (not Intel or Gfortran) gave the answer .TRUE. for the expression B .GT. A, where A and B were double precision, A was set to 1.D70 using a DATA statement, and B was read from the input string '1.D70' using a list-directed READ.
I am not sure if the more recent Fortran standards continue to permit such things to happen.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The standard is silent on such things, other than using the term "implementation-dependent approximation" in many places. I've seen that happen as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
By choosing to print using the format specifier '*', you make things look worse than they are. Instead of '*', try, for example, ES12.4.
A rule that we used to follow in our slide-rule days: "Display at most one significant digit more in the result than the digits in the input data".
Subtraction/addition of numbers with different signs may cause the number of significant digits to decrease.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Yes, perfectly reasonable. I think all those other compilers are using the same underlying conversions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I enjoyed this discussion tremendously. It raises some interesting points that really start from your first numerical analysis course.
I was in a shopping mall a few weeks ago, on the upper floor, 2nd floor in USA and 1st floor in UK. I could feel a strange movement in the floor. It passed quickly and it occurred irregularly - say 20 times in 2 hours. This conversation started me thinking about the floor movement, maxima, minima and resolution and how to tell if two numbers are the "same" .
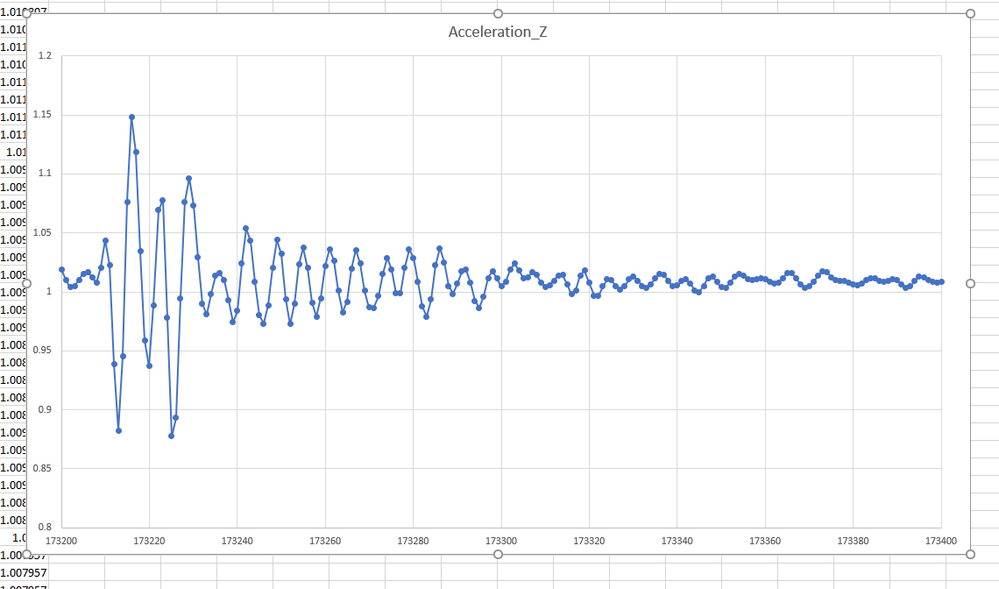
So yesterday, I went a spent an hour sitting in the food court, where I felt the movement strongly and recorded the data using an accelerometer.
I have a new program to determine the damping for structures, in Fortran of course. So I collected this data to review the program algorithm. It is challenging data.
-0.0191710107770644 g.
This is the typical acceleration number that comes from the machine. We have a few limits, the first is the step resolution, about 0.3 microg. Easy to find from a plot of the data sorted. We often have a problem with published papers when a theoretical engineer asks why the data is not smooth. One guy said it looked like a saw tooth. You cannot laugh because they are serious.
The second resolution is the thermal noise, 0.3 millig, you can see that at the end of the picture.
The interesting problem is the pulse shows up in the data.
The pulse is obvious, this picture is one tenth of a second, so the pulse lasts a 20th of a second. The large element is about a 200th of a second.
This thing has a range of about 0.2 g. About 100,000 times the resolution. So the first question is setting the data limits for the damping analysis. The second is the standard damping model assumes that you use the natural frequency, but here we have a device that is driving the structure - a saw toothed pattern will play hell with the FFT. THe FFT is going to be really short. All numerical problems.
The interesting challenge is fitting the standard damping model to the data. The asymmetry comes I suspect from the generator of the load not being balanced, like car tyres, but without the lead weights.
The interesting element is the constant in the exponential time element, we can measure that reasonably and it we measure it over months, we will get a good idea of the statistical data, the number gives a representation of the energy decay, moving to determine the damping factor as a % is the real question.
So thanks for the discussion, it gave me food for thought on this problem.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page