- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
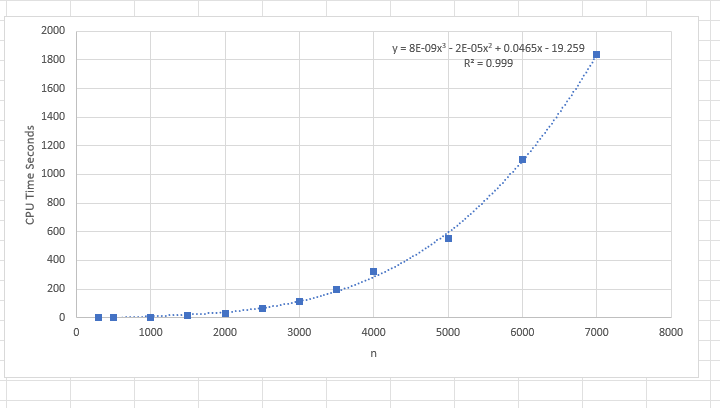
On the Fortran discourse site, there has been a discussion about matmul. The notes include a comparison of the results for different compilers and machines.
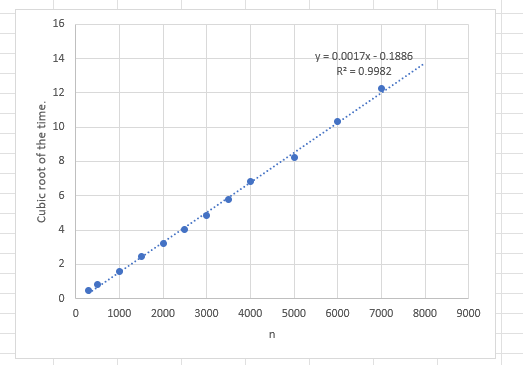
Running the program on IFORT in 32 bit mode, (no idea why 64 bit mode was slower). On a DELL Precision 5570 - Core I7 - 11850H with 32GB memory and a Samsung M2 drive, I get the analysis times shown on the graphs. The first graph is the run time as documented in the program and the second is the cubic root of the run time. A linear regression shows the time starts to climb above cubic past 6000 by a little bit.
No other programs running.
module maprod_mod
implicit none
private
public :: maprod, RP
integer, parameter :: RP = kind(0.0D0)
contains
function maprod(X, Y) result(Z)
real(RP), intent(in) :: X(:, :), Y(:, :)
real(RP), allocatable :: Z(:, :)
integer :: i, j, k
if (size(X, 2) /= size(Y, 1)) then
write (*, *) "Wrong size"
stop
end if
allocate (Z(size(X, 1), size(Y, 2)))
Z = 0.0_RP
do j = 1, size(Y, 2)
do i = 1, size(X, 1)
do k = 1, size(X, 2)
Z(i, j) = Z(i, j) + X(i, k) * Y(k, j)
end do
end do
end do
end function maprod
end module maprod_mod
program test_matmul
use, non_intrinsic :: maprod_mod, only : maprod, RP
implicit none
integer, parameter :: n = 7000
real(RP), allocatable :: A(:, :), B(:, :)
real :: start, finish
integer i, j, flag
write (*, *) 'Initialize'
allocate (A(n, n), B(n, n))
A = 1.0_RP
flag = 0
write (*, *) 'MATMUL'
call cpu_time(start)
do i = 1,n
do j = 1,n
if(A(I,J) .ne. 0.0_RP) then
flag = 1
end if
end do
end do
if(flag == 0) then
write (*, *) 'Zeros'
else
B = matmul(A, A)
end if
call cpu_time(finish)
write (*, *) 'Succeed'
write (*, *) 'Time in seconds:', finish - start ! The use of `cpu_time` is questionable. Just ignore it.
! Uncomment the following code if you would like to compare `matmul` and `maprod`.
!call cpu_time(start)
!B = maprod(A, A)
!call cpu_time(finish)
!write (*, *) 'Succeed'
!write (*, *) 'Time in seconds:', finish - start
end program test_matmul
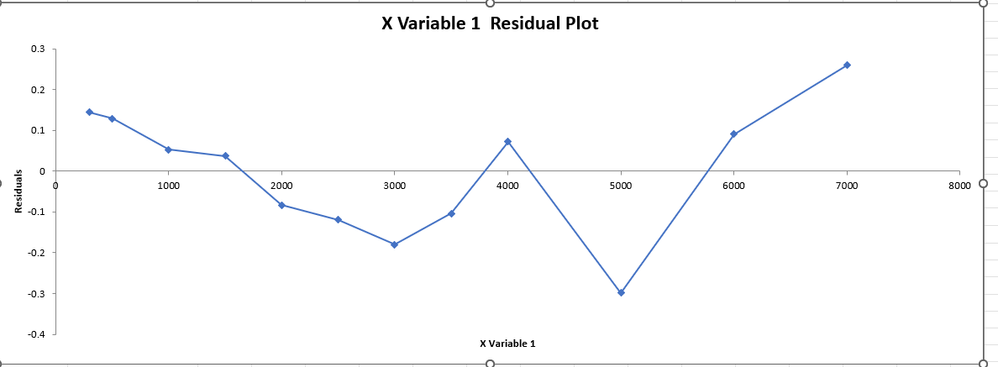
A linear regression on the second chart yields residuals that are interesting.
An algorithm that is O(n*n*n) is not optimal based on current publications.
Also if you search for any zero columns or rows, you should be able to reduce the run time.
Somewhere between 7000 and 10000 you hit a VM limit.
I changed the program so all the values are 1 and added in a check for all zeros on the matrix, which runs in 0.1 seconds.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
As Dr Fortran has noted, there are broken links on the Intel website.
The links point to generic pages, not the actual contents listed, some of those pages have 50 other links, and by the time you scan through you are lost. The links point to pretty simple things you should not have to then hunt for on your website.
Sample Picture of broken link - all do not work properly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
John,
I would be interested if you could provide your statistics using a preferred DO order.
! I do not like the DO order in this example
do j = 1, size(Y, 2)
do i = 1, size(X, 1)
do k = 1, size(X, 2)
Z(i, j) = Z(i, j) + X(i, k) * Y(k, j)
end do
end do
end do
! an improvement for memory access is
do j = 1, size(Y, 2)
do k = 1, size(X, 2)
do i = 1, size(X, 1)
Z(i, j) = Z(i, j) + X(i, k) * Y(k, j)
end do
end do
end do
! which using array syntax can become
do j = 1, size(Y, 2)
do k = 1, size(X, 2)
Z(:, j) = Z(:, j) + X(:, k) * Y(k, j)
end do
end do
This DO order is also suitable for !$OMP for larger examples
I have now included an adaption to the original post that tests different approaches for DO order, partitioning and OpenMP to improve L1 and L3 cache usage and SIMD instructions. These are only partly successful, so a start to identify some problems that remain.
Perhaps others can identify better approaches for improving efficiency for larger memory problems.
It is important to differentiate the cache inefficiency, that occurrs with larger n, from the O(n^3) op count.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page