- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have the two attached files. The main routine that does the work is determineC.
How do you decide if OPENMP will work on this structure and if it will, how do you implement it?
If I want to do very large numbers then I needed to take out the arrays, which means the program calculates the data JIT, rather then upfront.
The Intel example is much simpler than this code.
Thanks
JMN
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
John,
I am looking at your serial code. One of the issues with parallelization is your table of primes(nprimemax) and coeff(nprimemax), when parallelized cannot be filled in n=2, n+1, n+1, ... by each thread.
Further, your validity tests for the n'th prime candidate requires the 2nd through n-1th primes and coeff entries are valid (been calculated). This portion of your algorithm will need changing. I assume, for each prime candidate, a unique set of coeff will be generated. Therefore, coeff could be threadprivate whereas primes should be global.
Because the tables primes and coeff are initialized to 0, what you could do for parallelization is something like this
!$omp parallel clausesHere ! Note no DO
! Note all threads in this parallel region issue the same DO ii
DO ii=1, nprimemax, omp_get_num_threads() ! indexing with ii
i=ii+omp_get_thread_num() ! my i
if(i .gt. nprimemax) exit
... ! your code here
end DO
!$omp end parallel
...
*** During your verification for prime-ness test for i where you are testing against primes(someIndexBeforeN), when the expected value of a primes(...) contains a 0 this indicates some other thread hasn't filled in that cell. And in this case you wait for the cell to get filled. Note, the more iterations of the DO ii loop you perform, the fewer instances of waiting will occur.
Now, I am not going to do the work for you, but with the above hints it should get you going in the right direction.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@jimdempseyatthecove , thank you for the comments. I am sure with your notes I can now work it out. The real work now is just making it faster and also fixing the Patterns 2 and 3 to be like the main pattern that is not tied to an if clause set.
And a way to compress the data to get rid of the zeros' in the coefficient matrix. I will need to look at the methods used for eigenvalue matrix input.
This just started as a day dream in a car with a 14 yr old and then a desire to prove the day dream was incorrect. Looking for the number that does not fit the pattern, but I am now afraid it does not exist. And some free time.
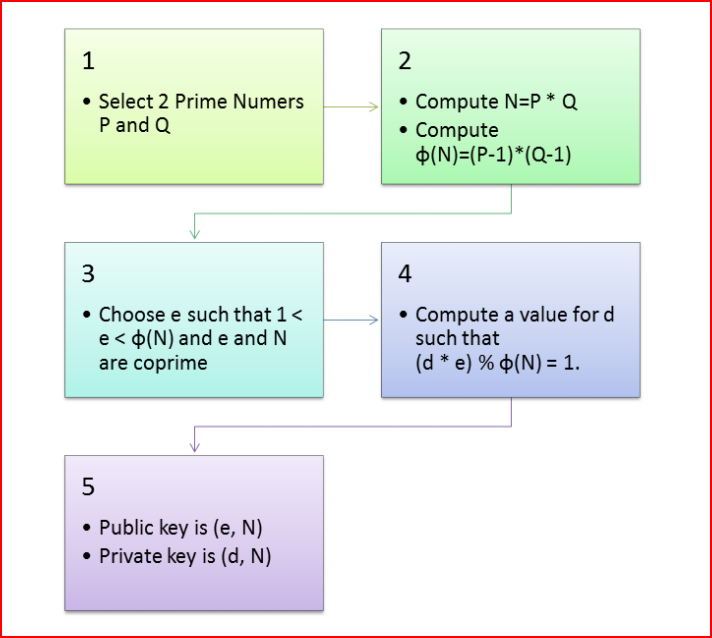
I was thinking about the use of primes, the RSA algorithm is an easy one to look at:
The interesting thing is if you consider the coefficient matrix, then the real first row is 1, which is all zeros. The pure math people want to argue one is not a prime, it is - it is just not a useful prime and saying it is causes all sorts of oddities in other theories, but it is the first prime.
P and Q in the drawing have to be primes so they are numbers of the form
[0 0 0 0 1] and [0 0 0 0 0 0 0 1]
If you multiply them together then the row for the N is simply
[0 0 0 0 1 0 0 1]
I have a table now that allows me to look up such numbers up to a largish integer number but not yet into the crypto stage, there are no primes or N's that do not fit that pattern, they represent at best 10% each of all the integers. Once someone gives you N if your coeff table is big enough looking up the P and Q is trivial, once you have P and Q you have P-1 and Q-1 and their coefficients, then the e is known, or so the picture says, assume it is correct, then finding d does not look that hard, if you have the coeff table. ( The argument is you do not have enough computing power or time to determine the coeff matrix.) that is the big if.
The argument that one needs to factorize anything in reverse is a nice dodge, but in reality the only trick now is throwing enough computing power at working out the coeff table. As long as you have a number representation like int nprimemax, then the table must be also calculable with the set of integers you create.
Of course I could be wrong and I continue on this quest just to show I am incorrect, that is the point of math and theorems, but in my deep mind I think that it is able to be done now.
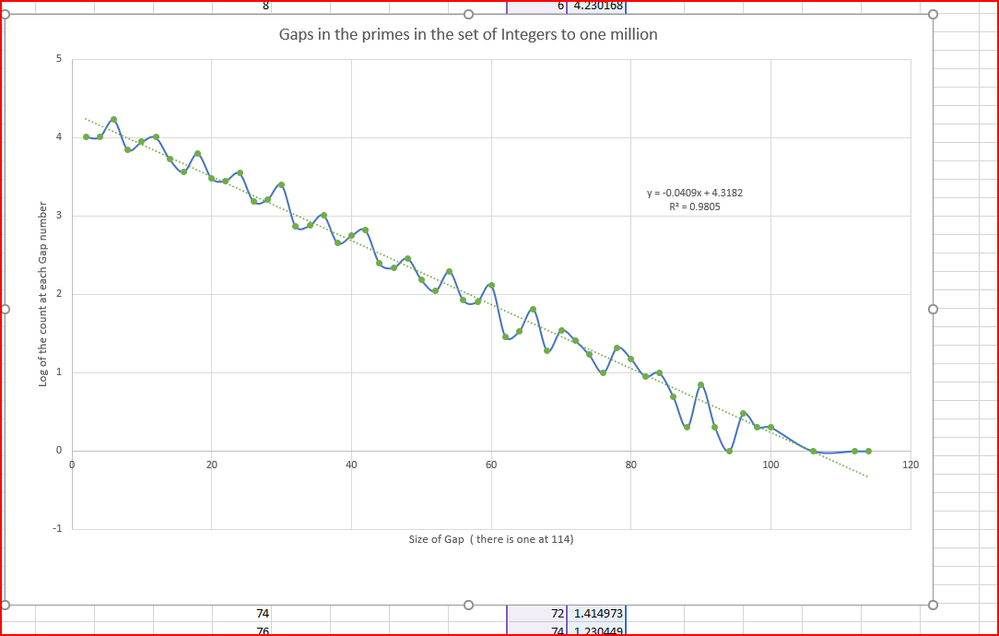
Another interesting graph is the graph of the count of the gaps in the primes. One sees the log linear graph and the small Fourier series for the "error" for want of a better word.
The only quaint bit is the difference in the if clause set for primes 2 and 3.
So far the program has correctly found the Mersenne primes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@jimdempseyatthecove , I need some test messages that are encoded in the RSA algorithm, it is not a real test unless the input data is blind, i.e. I do not know it.
The Fortran RSA algorithm is encoded on git hub, I have loaded it into a Intel SLN file, could you please do a couple of messages and publish the pubic part. The code is in the zip file. You might make the primes a little larger, as the test case is trivial from the current code.
I would at least like to see if the theory works or if it is just a mind figment.
Thanks
John
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page