- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Ever since Pure Math at ANU in 1975, prime numbers are of some interest.
I was reading an article on Prime Numbers, random prime numbers
I was taking my daughter for a drive, and I was playing with the random numbers in my head, and they do not appear to truly random.
If you consider the set of primes p1,p2, p3 etc..
then p4 + 1 is a composite, with
p4+1 = p1**c1*p2**c2*p3**c3
which can be cast as arrays.
The sets c(:,:) are determinant, they follow a set pattern for each c(i,:). The first few primes are shown in this format in the EXCEL chart.
I had a few spare minutes and I started to code a program to determine primes marching forward. It is rough and the counter patterns need to be properly coded, but can you call a random prime truly random if it is predictable from a simple pattern matrix.
program Primer
implicit none
integer, parameter :: n = 5
integer i
integer j
integer k
integer k1
integer L
integer prime(n)
integer primecount(n,n)
integer counter(n)
integer number
prime = 0
primecount = 0
prime(1) = 2
counter = 0
counter(1) = 1
do j = 1,n
do i =1,j
number = prime(1)**counter(1)*prime(2)**counter(2)
if(number .eq. prime(i)) then
write(*,100)i, j, (prime(k),k = 1,n),(counter(k1),k1=1,n), number
100 Format(2(i4," "),3(i5," ")," | ", 3(i5," ")," | ", i4)
counter(1) = counter(1) + 1
else
write(*,*)number
do L = 1,number-1
if(prime(L) == 0) then
prime(L) = number - 1
primecount(:,j-1) = counter(:)
counter = 0
if(L == 2) then
counter(1) = 1
counter(2) = 1
endif
exit
end if
end do
end if
end do
end do
end program primerProbably I am wrong.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
JMN wrote:
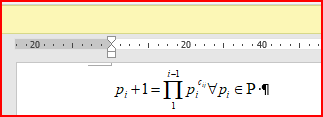
If you consider the set of primes p1,p2, p3 etc.. then p4 + 1 is a composite, with
p4+1 = p1**c1*p2**c2*p3**c3
The wording is rather vague. For the claim to be considered important, the four members p1,..,p4 should be assumed to be distinct. Is this a new conjecture from you, or do you have a reference to a theorem on which you think it is based? Are p1,...,p4 in increasing order?
Here are three counterexamples.
A. Assume p1,...,p4 are in increasing order. Then, p4+1 is even, so 2 is one of its factors. Unless you chose p1=2, the factor 2 is not a member of the set p1, p2, p3.
B. p1 = 2, p2 = 3, p3 = 5, p4 = 7; p4 + 1 = p1^3, and p2 and p3 are not factors of p4 + 1.
C. Take p4 = 7919, the last prime shown in the Wikipedia article. Then p4 + 1 = 2^4 . 3^2 . 5 . 11, which shows that p4 + 1 has four prime factors, Therefore, you cannot find any triplet p1, p2, p3 of primes that will suffice to satisfy the conjecture.
As it often happens, it is easier to find an example to disprove a false conjecture than to construct a proof of a true conjecture.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@mecej4 , I was playing with the idea, it is just fun to take my mind of programming and when driving slowly adding extra primes in my mind. A better representation is
The conjecture is that all primes are the integers that remain after you take away all the composites. The development of the composites leave holes in the set of integers. The interest is in the form of the each column set of the c(i,j) , so the column set of c(i,j) for the prime number 2 is
1 ,0 ,2 ,0 ,1 ,0 ,3 ,0 ,1 ,0 ,2 ,0 ,1 ,0 ,4 ,0 ,1 ,0 ,2 ,0 ,1 ,0 ,3 ,0 ,1 ,0 ,2 ,0 ,1 ,0 ,5 ,0 ,1 ,0 ,2 ,0 ,1 ,0 ,3 ,0 ,1 ,0 ,2 ,0 ,1 ,0 ,4 ,0 ,1 ,0 ,2 .... up to 54.
Visually -
So in the end I could not hold them in my head, so I moved to EXCEL, then you run into the time taken for each one and so at that stage I moved to look at a Fortran program, of course one is seeking the single number that proves the idea wrong, but to get there one needs to determine and program the for each column set of C(i,j)
The pattern for the 2 column is
| a | b | a | c | a | c | a | d | a | b | a | c |
where a = 1,0,2,0 b = 1,0,3,0 c = 1,0,4,0 d = 1,0,5,0 does this repeat forever with the third element increasing by 1.
And so on for all columns of c, just different forms.
If we use the equation above to represent all numbers then the primes are the ones where for p(i) the sum of the row c(i,j) up to i-1 is 1. Of course can we predict the form of the infinite series for each column of c - that makes it codable. The primes occur when the zeros in the a, b, c, d pattern across a row line up.
It is just fun. I was looking at was the idea codable to then look for the number that does not fit the pattern. That is the purpose of Fortran.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Well, the product representation that you provided in the small image (I think that the product is over j = 1,..., i-1, and the subscript on p should have been j, not i) is applicable to any composite integer, whether or not that integer is 1 + a prime. Furthermore, if you wish to seek and describe patterns in the c_ij, you have to specify that the primes be taken in some specific order, such as p_i > p_j if i > j.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I think the conjecture John is making is probabilistic not absolute.
Potentially, decryption methods could reduce time to solution by following the higher probabilistic paths?
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Jim:
The pattern in binary for one set is
0
1
0
10
0
1
0
11
It breaks into the groups of 4, which suggests the pattern exists in all bases, but I am not going to try and do any more.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@mecej4 -- All numbers can be represented as a multiplication of the primes that are less than the number (obviously)
so when I have 2 and 3 as primes I can represent 4 and 6, but not five so 5 is added to the prime class. I can find 5 just knowing 2 and 3. So now I have a different number representations for all integers as a set of the primes less than the number raised to a set of powers.
we can say 2 in the new representation is 1, 3 = 10, 4 = 2, 5 = 100 6 = 11, 7 = 1000, 8 = 3, 9 = 20 etc... it is weird to think about it, but then the numbers looked at vertically have patterns.
The conjecture is that each set has a pattern.
I was struggling with the mathematical representation of the idea, I had a shot at it in the early post, but the idea is if coded it makes it easy and I thought a different way to search for primes, at the moment we do a reverse search.
Jim: I am of the opinion it holds to infinity, but the beauty of theorems is to find out you are wrong. I am happy to be proven wrong, the fun is in the search and the coding.
What if I am not wrong?
The next challenge is coding the patterns?
Plus who else but you lot would you want to have this much fun with - only my daughters and only 1 is interested in math.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
program Primer
implicit none
integer, parameter :: n = 12
integer i
integer j
integer k
integer k1
integer L
integer sum
integer prime(n)
integer composite(2*n)
integer primecount(n,n)
integer counter(n)
integer number
integer Llast
prime = 0
primecount = 0
prime(1) = 2
counter = 0
Llast = 1
counter(1) = 1
do j = 1,n
do i =1,j
number = prime(1)**counter(1)*prime(2)**counter(2)*prime(3)**counter(3)*prime(4)**counter(4)*prime(5)**counter(5)*prime(6)**counter(6)
write(*,*)"Number 1 :: ", number
sum = counter(1) + counter(2) + counter(3) + counter(4) + counter(5)
if(sum > 1) then
composite(number) = 1
end if
if(number .eq. prime(i)) then
write(*,100)i, j, (prime(k),k = 1,n),(counter(k1),k1=1,n), number
100 Format(2(i4," "),3(i5," ")," | ", 3(i5," ")," | ", i4)
counter(1) = counter(1) + 1
else
write(*,*)"Number 2 :: ", number
composite(number) = 1
do L = 1,number-1
write(*,*)" L :: ", L
if(prime(L) == 0) then
if(composite(number - 1 ) == 0 .or. composite(number) .ne. 1) then
prime(L) = number - 1
primecount(:,j-1) = counter(:)
counter = 0
endif
if(Llast == 1) then
counter(1) = 0
counter(2) = 1
Llast = 2
elseif(Llast == 2) then
counter(1) = 3
counter(2) = 0
counter(3) = 0
Llast = 3
elseif(Llast == 3) then
counter(1) = 0
counter(2) = 2
counter(3) = 0
counter(4) = 0
Llast = 4
elseif(Llast == 4) then
counter(1) = 1
counter(2) = 0
counter(3) = 1
counter(4) = 0
Llast = 5
elseif(Llast == 5) then
counter(1) = 2
counter(2) = 1
counter(3) = 0
counter(4) = 0
Llast = 6
elseif(Llast == 6) then
counter(1) = 1
counter(2) = 0
counter(3) = 0
counter(4) = 1
counter(5) = 0
Llast = 7
elseif(Llast == 7) then
counter(1) = 0
counter(2) = 1
counter(3) = 1
counter(4) = 0
counter(5) = 0
Llast = 8
elseif(Llast == This is an extremely badly coded method, but it works to 19 and shows me how to improve it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Well I took a day off to properly code the prime program.
It appears to work a treat.
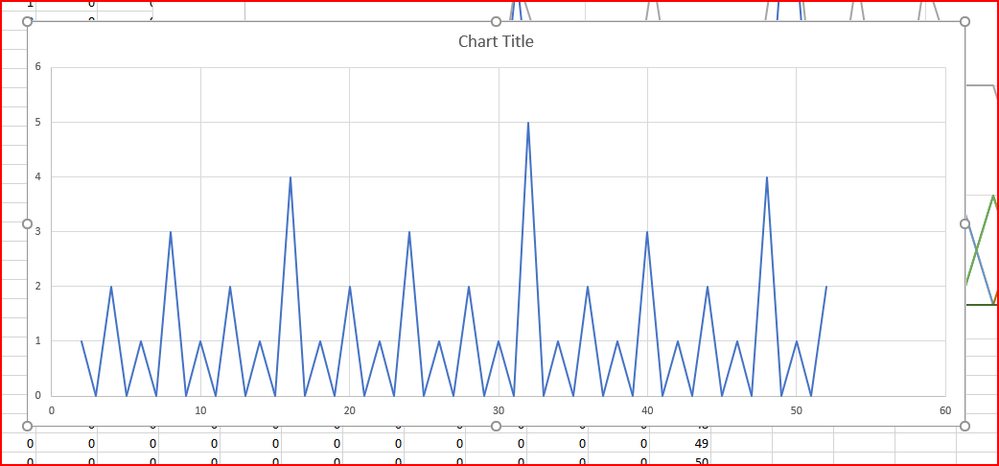
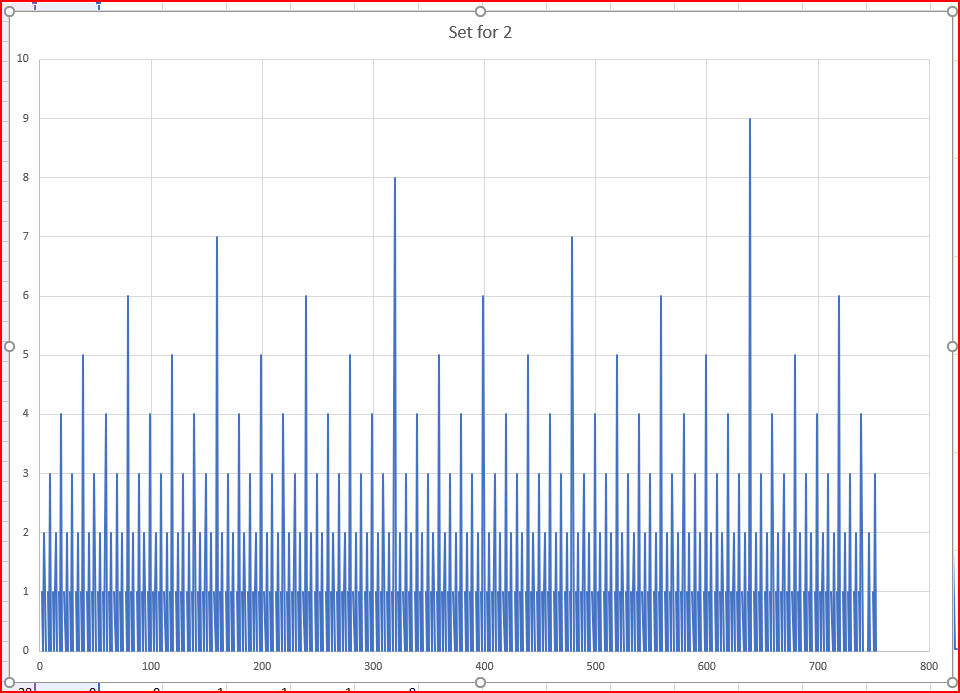
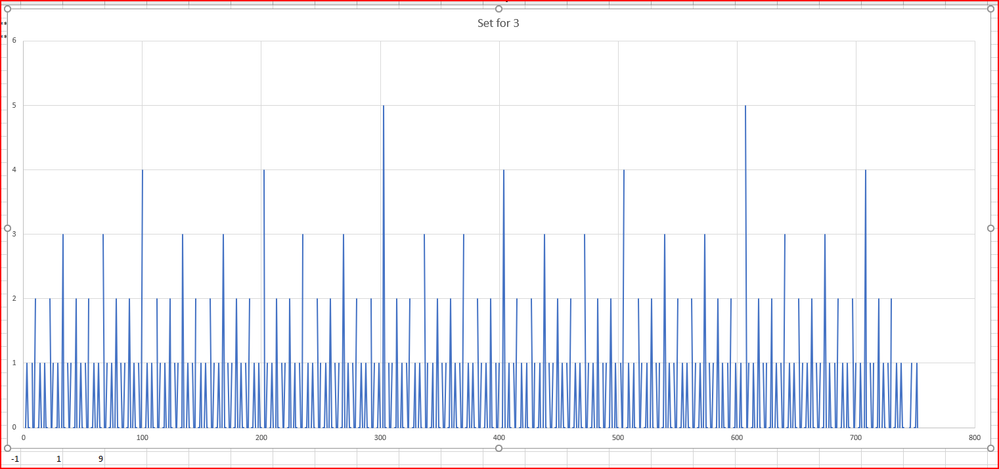
There are three patterns to the numbers. The first pattern is for the set of 2's, the second is for the set of 3's and the last pattern so far is for all the others.
The last pattern appears to work perfectly, the 2's I have the algorithm sorted nicely - it is evident in the code, the threes I have made a dog's breakfast of the code and I need to simplify it. It should have a similar structure to the 2's. it would be trivial to make the code self correcting, but I am not going to do that I want to see the patterns develop.
I have the code running to 600 as I sort of the 2's and 3's pattern and code it.
The patterns are repetitive, see the graphs
There is no great randomness to the primes, they are merely the product of a set of waves of relatively fixed numbers.
The argument that 1 is not a prime for a variety of reasons is interesting, but in reality it is the zeroth prime as it is product of all primes raised to the zeroth power. Otherwise you need to say that 0 is not an integer.
I assume this is not new, but it was a fun way to waste a day. As I was doing it I gave a name to the set of numbers in the matrix, the Field Numbers after the great prof who taught me Fluid Mechanics and supervised my Honors work.
It is a minor bit of trivial code to determine the Mersenne primes.
Thanks to @mecej4 , I copied the style from Magni for the structure and the Types. There is some miscellaneous garbage in the files from Magni.
The program is designed to stop when it finds an error in the patterns.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There are simple modulo patterns underneath the set2 and the set3.
It has been a long and fun day.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I found the patterns, easy to extend, I ran into the problem that I have been wasteful on the arrays and I am stuck with the 2GB limit, it will comfortably do 15000 integers in 70 seconds, I print the results to the screen which is always slow. I get the Mersenne Primes.
I could not get heaps array to work, help needed.
There appear to be 3 patterns to the coefficients, one for the 2's, one for the 3's and one for the rest, once I had that sorted it runs quite nicely.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
>>The first pattern is for the set of 2's, the second is for the set of 3's and the last pattern...
You've made a presumption that the true number base is base 10. What does your frequency distribution look like using different number bases? Do they show a similar distribution?
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You are driving along with a 14 year old in the back watching a TV show that is in Korean and there is 3 hours to go you need something to think about. Primes are easy as they are simple and beautiful.
I was thinking about the first group, 3, 5, 7, which makes you logically think that 9 should logically, deep in your mind, be a prime, I mean of any number 9 not being a prime is so sad. Apology - but a book title for a mystery should be "Nine not a prime" but it should be -- a murder mystery with a nun, priest and a Fortran programmer. The victim has a punch card pinned with their chest with a spindle
That got me thinking about the components. Blast 3 squared being 9.
You look at them as you start to wonder why there is not a pattern? We see the same thing in FFT results, you spend many days looking for patterns in things that look random, but are not. Then have the fun of explaining them.
The problem to me is explaining composites as a number made up of primes, ie primes are different, but what if they are not that different.
So a composite is num = a*b or a**2*b
Now extend this to mean that number is a complete infinite set of primes each raised to an integer power and multiplied together - a product. Once you think this, it suggests that if you have a prime raised to zero you have one, so a composite is an infinite set of primes raised to a set of powers.
We can represent the set for each number whether composite of prime as a group such as
1000000000 ...........
Unfortunately I use them in Fortran so we read the number as increasing from left to right, so this number represents 2 to the first power and all the rest to zeroth power. For simplicity terminate the printing at the first zero in the infinite remaining set.
So 01 is 3, 2 is 4, 001 is five, 11 is six and 0001 is seven. Extend them to a matrix
1 0 0 0
0 1 0 0
2 0 0 0
0 0 1 0
1 1 0 0
0 0 0 1
The numbers look weird until you get enough of them. primes are just the rows that if you sum all components in the matrix sum to one. It is actually a simple test for primeness, it can be done marching forward, all you need is the start with 2 and 3.
Now if you plot the columns in EXCEL you see a nice set of patterns.
I did the first 54 in EXCEL and got really bored and it is hard mentally. Last week was spent on a challenging FFT and occasionally taking a break to read this forum and the Guardian. To the poor people who read this forum, I apologize for inflicting this stuff upon your soul.
So I took a break and decided to have some fun and just code the primes properly. I grabbed the good stuff @mecej4 gave me for Magni, thank you. The only challenge is the form of the patterns, but the program provided a way to allow the program to tel you the errors in your patterns. The twos pattern is simple
!-------------------------------------------------------------------------------------------------
!
!
!
!-------------------------------------------------------------------------------------------------
subroutine Pattern_2(i, cj, cjI)
implicit none
integer i
integer cj
integer cjI
integer j
integer k
integer count
cj = 0
count = 0
if(i .eq. 1791) then
write(sw,*)"here"
endif
if(mod(i,4) == 1) then
cj = 1
else if(mod(i,4) == 2) then
cj = 0
else if(mod(i,4) == 3) then
cj = 2
count = 0
do k = 7, nprimemax,8
count = count + 1
if(i == k) then
cj = 3
if(mod(count,4) == 2) then ! if(count == 2 .or. count == 6 .or. count == 10 .or. count == 14 .or. count == 18 .or. count == 22 .or. count == 26 .or. count == 30 .or. count == 34 .or. count == 38 .or. count == 42 .or. count == 46 .or. count == 50 .or. count == 54 .or. count == 58 .or. count == 62 .or. count == 66 .or. count == 70 .or. count == 74 .or. count == 78 .or. count == 82 &
cj = cj + 1 ! .or. count == 86 .or. count == 90.or. count == 94 .or. count == 96 .or. count == 98) then
else if(mod(count,8) == 4) then ! else if(count == 4 .or. count == 12 .or. count == 20 .or. count == 28 .or. count == 36 .or. count == 44 .or. count == 52 .or. count == 60 .or. count == 68 .or. count == 76 .or. count == 84 .or. count == 92 .or. count == 100) then
cj = cj + 2
else if(mod(count,16) ==
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You can see the method used to develop the patterns in the comments on the right. I can assure that was the boring part.
The 3's pattern was difficult, I started badly, but once I had the 2's I went back and tried the same thing at midnight last night with the 3's and in about an hour had the following,
!-------------------------------------------------------------------------------------------------
!
!
!
!-------------------------------------------------------------------------------------------------
subroutine Pattern_3(i, cj, cjI, counter, root)
implicit none
integer i
integer cj
integer cjI
integer j
integer k
integer count
integer counter
integer modD
integer modE
integer modF
integer modG
integer num
integer prime
integer root
integer seek
integer mark
integer cH
cj = 0
count = 0
prime = 3
mark = 1
cH = 0
seek = 17
if(seek == i) then
write(*,*)"here"
end if
do k = 1,nprimemax
if(k == i) then
if(mod(mark,6561) == 6560) then
ch = 8
else if(mod(mark,2187) == 2186) then
cH = 7
else if(mod(mark,729) == 728) then
cH = 6
else if(mod(mark,243) == 242) then
cH = 5
else if(mod(mark,81) == 80) then
cH = 4
else if (mod(mark,27) .eq. 26) then
cH = 3
else if(mod(mark,9) == The descending order is important.
The final pattern was really simple.
!-------------------------------------------------------------------------------------------------
!
!
!
!-------------------------------------------------------------------------------------------------
subroutine pattern(m, prime, coeff)
implicit none
integer m
integer prime
integer i
integer coeff(nprimemax)
integer num
integer k
write(sw,100)prime
100 Format(//," Coefficients for prime :: ",i6,//,"-------------------------------------------------------------------------",//)
do i = 1, nprimemax
if(i == 1 .or. i <= prime - 1) then
coeff(i) = 0
else
coeff(i) = 0
endif
if(mod((i+1),prime) == 0) then
coeff(i) = 1
endif
end do
do i = 1, nprimemax
num = prime**i
if(num > nprimemax) then
exit
end if
coeff(num-1) = i
if(2*num .lt. nprimemax) then
do k = 2,nprimemax
if(k*num - 1 < nprimemax) then
coeff(k*num - 1) = i
end if
end do
end if
end do
do i = 1, nprimemax
write(sw,*)i,coeff(i)
end do
return
end subroutine pattern
All other primes so far follow this pattern.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page