- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi all,
I'm using the Microsoft Fortran Compiler of Fortran Power station 4.0 under windows 98. I've written a program which leads to an error in Fortran Power Station ,but it works correctly in Code Blocks or Visual Studio (Intel Fortran) compilers. I've searched for this error in some forums and i was told that "This particular error is due to something like a temporary file that can't be deleted, or an executable file that can't be written. Windows 95 seems to have this problem a lot. Usually you can delete the Debug and Release directories, or exit the compiler and restart it. That should fix your errors. " which isn't helpful. So i have two questions. Firstly, why a particular code may have errors in one compiler, but no ones in the others?secondly, how can i fix this particular error?
Thanks in advance
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The Fortran standard specifies rules that can be applied to a particular program to determine whether or not that program source is "conformant" with the standard. With few exceptions, the compile time and run time behavior of a non-conformant program is not specified by the standard. In colloquial terms, anything can happen. Compiler authors usually strive to make their product capable of going beyond what the standard requires, adding features to locate and diagnose errors.
That a program runs without any error messages is no proof of its correctness. A faulty program may even give correct results; nevertheless, it is faulty, and the fault may rear its head when that program is recompiled with a different (or a newer edition of the same) compiler.
"How can I fix this particular error?": start by describing the particular error; provide enough information to enable us to reproduce the error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Fortran Power Station was a notoriously buggy compiler. As you have a more modern and reliable compiler, it seems unproductive to worry about this, even if you are keeping the old installation for historical reasons.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Can you suggest me a powerful compiler? I'm also seeing for a compiler which has IMSL libraries like Fortran power station or the way which one can join them to their compilers?
Thank a lot for your time and comments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There seem to be many preconceptions thrashing about. First of all, forget Powerstation. According to what you wrote, it fails to compile one of your sources because of an internal compiler error. Your program is quite small, so there is no point in looking for a SuperPowerStation compiler, nor is it clear what you mean by "powerful compiler".
We do not know what your program calculates, the mathematical description of the problem or the nature of the algorithm used. We could try to decipher what these might be by perusing the source code, but that would be a waste of time when you could easily tell us in a few words.
Intel Fortran can be bought with IMSL, but that can be expensive. At this point, it is not even clear that you need the capabilities of IMSL that are not available in MKL.
Finally, given an algorithm with some tuning parameters, it is perfectly reasonable that the algorithm diverges for certain values of those parameters. For example, the forward difference method for solving the diffusion equation is unstable for α Δt / Δx2 > 1/2, where α is the diffusivity, Δt and Δx are the discrete step-sizes of t and x.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
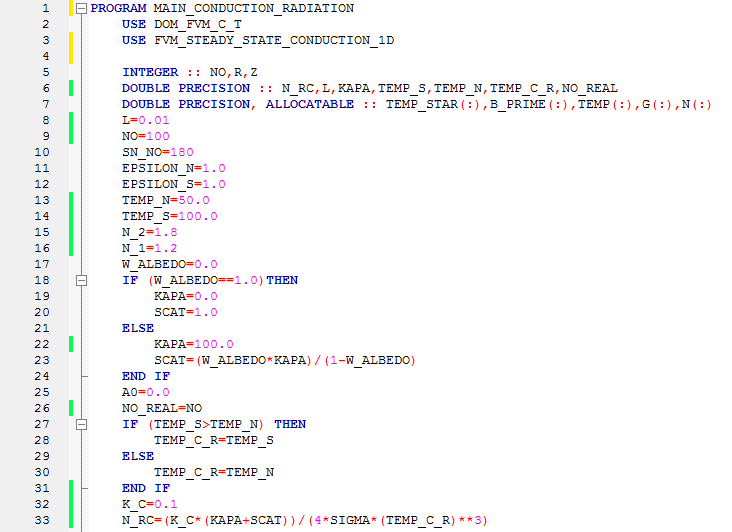
A quick glance at the code in #4 shows the absence of "IMPLICIT NONE" so all those undeclared variables take default types based on the first letter. Thus we have a mix of single and double precision in the equations. Also I see things like N_2=1.8 , do we really want to assign a real to an integer variable or is N_2 mean to be a real? Also integer constants (e.g. 4) in real expressions can lead to "unexpected" results I would always use 4.0 or 4.0d0.
I agree with mecej4/Tim why use Powerstation, it is a long dead and buggy product. But if you must use it then at least "clean up" your code.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
With implicit variables, and N_1 not being explicitly declared, N_1 is equivalent to
INTEGER(1) :: N ! byte sized integer
There may be a switch to turn off the suffix.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
jimdempseyatthecove wrote:
With implicit variables, and N_1 not being explicitly declared, N_1 is equivalent to
INTEGER(1) :: N ! byte sized integer
No, that is not the case. The underscore kind suffix is for literal constants only. It doesn't apply to identifiers. N_1 is simply default INTEGER implicitly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
First of all, i simply introduce this program.Here i tried to couple the conduction and radiation heat transfer together in a one dimensional medium .The TEMP_N and TEMP_N are the boundary temperatures and N_1 and N_2 are refractive indices at boundaries. Also the other variables are some heat transfer coefficients. Some variables like N_1 or N_2 are defined in " DOM_FVM_C_T " or " FVM_STEADY_STATE_CONDUCTION_1D " modules before and there is no need to define their type here in the main program. Moreover, N_1 is real variable which defined before and i should note that 1 in N_1 is a subscript and nothing else. Finally, i use IMPLICIT NONE, though the program again diverge for some high values of the temperatures (TEMP_N & TEMP_S). Would you mind downloading the attachments to see whether the algorithm or the syntax are correct?. Any suggestions will be greatly appreciated.
Thanks in advance!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sina, there are many separate issues here, as I attempted to convey to you in #6. Briefly, the questions are:
- What is the physical problem being solved? We need a precise description and the simplifying assumptions and justifications, and a listing of the governing equations.
- What is the numerical method used to solve the equations?
- Does the program correctly implement the numerical method?
- Is the compiler being used correctly, and is its behavior correct?
- Are the results reasonable? Are they correct?
Issue 4 is the only one that you may reasonably expect to be addressed in this forum. Nevertheless, I happen to have some knowledge of heat transfer, and I am able to make the following general description, which may help you to understand why, for certain values of the two parameters that you mentioned, the solution is unbounded.
When a solid is experiencing heat conduction with an internal heat source, the intensity of the source q (heating rate per unit volume, W/m3) is temperature-dependent and q increases with T, there is a critical value of dq/dT beyond which the steady state temperature is unbounded. Consider a metal wire with fixed electric current passing through it, made of a material with positive temperature-coefficient of resistivity (i.e., if ρ is the specific resistance of the conductor, and dρ/dT > 0), there is a critical current which, if reached, will cause the wire to melt and fail.
A more severe physical problem of this nature is fission reactor meltdown (Chernobyl!).
You do not have electric heating but you do have a radiation source term and that term is temperature dependent. Whether my explanation applies to your problem or not is something that is impossible to comment upon without your giving an answer to Question 1 above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Just to cover all corners, I loaded FPS4 on a Windows 10-X64 laptop and built your program with it. Not only did the compilation complete without errors, but also the output data file was nearly identical (13 digits agree) to that produced by Intel Fortran XE 2015.
It is possible that your installation of FPS4 has become corrupted or your version is slightly different from mine.
However, as noted elsewhere in this thread, let us let FPS4 R.I.P. !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your comment. Let me describe the physical problem more. I tried to write a program which solve heat equation for a one dimensional absorbing emitting and scattering semi-transparent slab with variable spatial refractive index at radiative conductive coupling.Consideration is given to a system consisting of two diffuse, non black, isothermal parallel plates separated by a finite distance.The conservation of energy equation for steady state, one-dimensional simultaneous heat conduction and radiation in an absorbing, emitting, and scattering medium is: 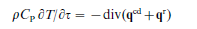
I should valid this program with a paper which the temperatures of boundaries are TEMP_S=1000 and TEMP_S=1500,and other characteristics are kapa=100, K_C=1, N_1=1.2 and N_2=1.8 .
Now the problem is that when i increase the magnitude of temperatures from an assumed values of TEMP_S=100 and TEMP_S=50 to the grater ones, the program start diverging.
I personally think that the coefficients( A & B) of linear set of equations ( [temp]= ) which are defined in the" FVM_STEADY_STATE_CONDUCTION_1D " module are not enough smooth in some cases and due to some numerical bad effect program diverges. I'm pretty sure about the algorithm, yet i can't handle this problem.
Any suggestions will be greatly appreciated.
Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The set of equations that you need to solve are nonlinear. Your algorithm consists of breaking the equations into two groups.
1. The first group consists of explicit equations for the radiation terms in terms of temperatures. You solve these simply by substituting guessed temperatures.
2. You then substitute the resulting radiation terms into the second group, which come from discretizing the heat equation, and solve the simultaneous linear equations to obtain (hopefully) improved temperatures.
3. You compare the improved temperatures with the previous set of values and, if not satisfied, go back to Step 1.
This algorithm converges in a few iterations for your starting case, with Temp_N = 50 and Temp_S = 100. In an attempt to extend the calculation to higher values of these parameters, I found that simple parameter continuation works -- but only up to a point. That is, gradually increasing Temp_N and Temp_S, each time using the converged solution for the previous values of Temp_N and Temp_S as the initial "guess".enabled me to reach Temp_N = 400 and Temp_S = 800. However, the number of iterations required increased substantially.
I conclude that you should use a better algorithm to solve the nonlinear equations. Consider, for example, the TRNLSP routine that is included in the MKL library.
P.S.: In #13, you have "TEMP_S=1000 and TEMP_S=1500"; please correct this (one of the two TEMP_S -> TEMP_N)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I think the set of LINEAR equations must be solved in order to improve temperature filed from energy equation (you called it second group). When radiation term is achieved from explicit equations for the radiation(RTE), then this part is added to the heat equation as a source term. After that the discretized form of heat equation plus source term which are a linear set of equations must be solve. In order to solve this i choose the direct method called gauss_jordan elimination. Actually i consider that there is no nonlinear set of equation here, is there? . I can extend the parameters to reach Temp_N = 1500 and Temp_S = 1000 when N_1=1 and/or N_2=1 are unit but for Ex: with N_1=1.2 and N_2=1.8 program diverges . Now i'm thinking about to use standard libraries subroutines to solve this set of equations and actually that is why i try to use FSP4 because of its IMSL libraries . So could you please tell me how to add MATH KERNEL libraries to the Intel Fortran (Visual Studio2010)?
Also what do you mean by "P.S.: In #13, you have "TEMP_S=1000 and TEMP_S=1500"; please correct this (one of the two TEMP_S -> TEMP_N)" ?
Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Let me explain the issue of nonlinearity in terms of a single-variable problem. Let x be the unknown. You have an equation to solve of the form a x = f(x), where f is nonlinear. What you have done is to recast this equation as
a x = b, b = f(x)
Since the name 'b' suggests a constant, the first equation deceptively appears to be linear. However, b still depends on the unknown x.
You solve this equation with the iteration scheme:
0. Guess x0, set i = 0.
1. Evaluate bi = f(xi) explicitly.
2. Solve a xi+1 = bi .
3. If xi and xi+1 are not sufficiently close, increment i and go to Step 1.
Many methods for solving nonlinear equations consist of similar sequences of solving linear equations. It is important to note that ad hoc iterative methods such as the one you used may not converge at all, or may converge only for certain guess values, or convergence may occur only for certain ranges of parameter values. Look up "Julia sets" in Wikipedia or elsewhere.
_________________
"TEMP_S=1000 and TEMP_S=1500": read carefully; you have "TEMP_S" twice. Surely, it cannot have two different values at the same time?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You are right. The heat equation is - div(qc) - div(qr)=0 which - div(qr) is the source term,that is S= - div(qr)=4*KAPA*SIGMA*TEMP**4 - G .The discretize form of this equation is [TEMP] = , B = f(TEMP). Here B is nonlinear in relation with TEMP (temperature), so what i should do is linearizing the radiative source term. In the source term linearization we transform S to S_c+S_p*TEMP in such a way which S_p<=0.0 .
S=S_c+S_p*TEMP , TEMP_STAR is the previous iteration value of TEMP. In this case we do it as follows:
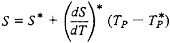
R.H.S : S=4*KAPA*SIGMA*TEMP**4 - G
L.H.S : S_c+S_p*TEMP= (12*KAPA*SIGMA*TEMP_STAR**4 +KAPA*G) +(-16*KAPA*SIGMA*TEMP_STAR**3)*TEMP
by use of this the B coefficients become linear in relation to TEMP a then one can solve the linear set of equation. By the way is there any need to solve nonlinear set of equations?
Your last comment is very helpful, let me try another guess values.
Thanks for your time and comments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
This may or may not be an issue (mecej4 can comment on this).
You have:
DOUBLE PRECISION ,PARAMETER :: EPSILON = 1.0E-6
which is a constant. A problem that is often encountered with a fixed epsilon, is the convergence routine will work for inputs/outputs of a limited range (magnitudes). A better approach is to determine the magnitude of the numbers your are manipulating, then construct an epsilon for the desire significance. Something like this:
REAL(8) :: WITHIN ... WITHIN = 100.0D ! WITHIN 2 SIGNIFICANT DIGITS OF PRECISION ... IF((A-B) < EPSILON(A)*A*WITHIN) CONVERGE = .TRUE.
What the above is doing is comparing the difference between a and b (prior iteration and current iteration??) and
(smallest number relative to 1.0 of type A that can be added to 1.0 of type A that can represent a different number)
then scale it to the magnitude of A (*A) to get the least significant bit value
then scale it again (*WITHIN) to get the convergence limit
Of course you can "optimize" this by:
REAL(8) :: WITHIN REAL(8) :: MyEpsilon ... WITHIN = 100.0_8 ! WITHIN 2 SIGNIFICANT DIGITS OF PRECISION MyEpsilon = EPSILION(A)*WITHIN ... IF((A-B) < A*MyEpsilon) CONVERGE = .TRUE.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
First of all, than you for your helpful comment.I wrote a program which contains two main modules and a main program which i attached them.Although it works correctly in Code Blocks and Visual Studio (Intel Fortran) compilers, it results in "Command line error D2013: internal compiler error" in Fortran Power station. I don't know how to figure this error out. Any ideas will be greatly appreciated.
second and more important questions is why does the outlet data lead to NAN or infinity when the magnitude of the TEMP_N and/or TEMP_S are increased. I'm pretty sure that there is no 0/0 in the program,yet program begins to diverge! I also pretty sure about the algorithm, because with some values of these two parameters the program gives correct answers, but i can't generalize it for all possible values of TEMP_N and TEMP_S .Can you help me with that.
thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
With suitable modifications made to the comments of #18 to accommodate negative values of the variables concerned (e.g., by applying the ABS() function), the advice given there could be quite helpful. Most of the algorithms and code in ACM-TOMS and in libraries such as IMSL and NAG allow the user to specify both relative and absolute tolerances for checking the convergence of iterative algorithms.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you all for your comments and suggestions. Finally i can handle it.
good luck.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page