- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I built my own class for CSR3 matrices for Mkl Pardiso and I have to know how Mkl knows the length of arrays (values and columnIndex ):
- Is it done by rowIndex[number_of_rows]?
- Is it done by some information provided by mkl_alloc?
I know it seems a very stupid question but it's a whole month that I'm working on this problem:
1st case
- I preallocate the matrix with an estimated number of nonzeros (element that are not really initialized has a flag that say that are not used)
- I compress it, deleting all unused/uninitialized elements
2nd case
- I preallocate the matrix*
- I read the matrix from an external file
The two matrices at the end are ABSOLUTELY IDENTICAL. It changes the way they're allocated first.
The case one works very well, but after a random number of steps of the dynamic problem it has a huge residual (sometimes >e+14, yes it's a plus)! At that time I write the matrix on a file, I read it back to another matrix and then I give this matrix to Pardiso again and puff! All is perfect again! Residual e-15!
Do you have any suggestion?
Many thanks,
Dario
*in the 2nd case it works also if I preallocate whatever number of nonzero and then I compress. It works well at anytime!
** comparing IPARM output I noticed that or iparm(63) one-indexed it changes everytime but in the step where I face the problem there's a -1 in the 1st case and 0 in the second case... I don't know if it is useful
Here my settings: ONE-indexed
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
/*IPARM easy settings*/
IPARM(1) = 1; /* No default values for solver */
IPARM(6) = 0; /* Write solution on u */
IPARM(12) = 0; /* Solve with transposed/conjugate transposed matrix [def: 0, solve simply A*x=b]*/
IPARM(18) = -1; /* Report number of nonzeros */
IPARM(19) = -1; /* Report number of floating point operations */
IPARM(35) = 1; /* Zero based indexing */
IPARM(27) = 1; /* Matrix checker */
IPARM(28) = 0; /* Double precision */
IPARM(36) = 0; /* Schur complement matrix computation control [def:0, do not compute Schur] */
IPARM(56) = 0; /* Diagonal and pivoting control [def:0, disabled] */
IPARM(60) = 0; /* In-Core (OC) / Out-Of-Core (OOC) switch [def:0, IC mode] */
/* IPARM fine settings */
IPARM(2) = 2; /* Fill-in reducing ordering [def:2] */
IPARM(4) = 0; /* Preconditioned CGS/CG [def:0] - HIGHLY RECOMMENDED */
IPARM(5) = 0; /* User fill-in reducing permutation [def:0, default filling]*/
IPARM(8) = 10; /* Maximum number of iterative refinement steps */
IPARM(10) = 13; /* Perturb the pivot elements with 1E-value [def:13 for unsymm/8 for symm, 1e-13 perturbation]*/
IPARM(11) = 1; /* Scaling MPS [def: 1 for unsym/0 for sym, scaling enabled] */
IPARM(13) = 1; /* Maximum weighted matching algorithm [def: 1 for nonsymmetric matrices, enabled) */
IPARM(21) = 1; /* Pivoting for symmetric indefinite matrices */
IPARM(24) = 0; /* Parallel factorization control [def:0, classic algorithm] */
IPARM(25) = 0; /* Parallel/sequential solve control [def:0, parallel] */
IPARM(31) = 0; /* ADV Partial solve and computing selected components of the solution vectors [def:0, disable]*/
IPARM(34) = 0; /* ADV Optimal number of threads for conditional numerical reproducibility (CNR) mode [def:0, disable]*/
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dario, here are some observations to help you. Your matrices have many zero entries, and these zero entries do two bad things. A sparse matrix should not contain any, unless required as a placeholder (e.g., a diagonal element of a symmetric or structurally symmetric matrix). I removed the zero entries, and put your data into the following format (files with .CSR suffix):
Line-1: title Line-2: n,nnz,index base Lines 3 to n+2 : rowptr,rhs, i=1:n Lines n+3 to n+2+nnz : col(1:nnz),val(1:nnz)
I found that the removal of the zero-value matrix elements greatly improved the results from Pardiso. The residual norm remains at or below 10-7, and the solutions agree to six or more digits when the RHS values are switched from 12 to "24" digits. Note that double precision does not give you more than 16 digits of precision, even if you print out 24 digits.
The second issue is one that I am unable to address: a good fraction of the solution values are zero. Perhaps you can tell from your understanding of the physics which xi values should come out to zero, even before performing the solution. If so, you can eliminate the columns corresponding to those x values, and discard a number of equations equal in number to the count of zero-valued solutions.
For example, Beam35 has 270 unknowns and 3276 matrix entries. However, only 2497 of those entries are non-zero, and 105 of the 270 elements of the solution are zero.
The .CSR files and files with the solution vectors are in the attached zip file.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
If I can guess what you're asking, the length (number of non-zeros) of each row is the difference between neighboring row or column indices. There are plenty of examples both on Intel web pages e.g. https://software.intel.com/en-us/node/471374 (which may contain misleading typos) and non-Intel ones.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
No no no! I know how CSR3 format works and how element are arranged. I know that the question is subtle, but the problem I'm having it's incredibly strange.
I'm asking if MKL in its internal algorithm has a particular way to read the matrix (maybe it relies also on the size of the arrays allocated?). I know it's strange, but I have two matrices that are exactly the same but that give different results (one gives huge residuals, the other works normally).
I checked them many times, the only difference it's that the element in the second matrix are written copying each element of the three arrays directly. In the fist matrix elements are written (altough already allocated in memory) in a random sequence.
But when I call the Pardiso solver and I give him the addresses of the arrays, the arrays are absolutely the same!
I'm stuck in this problem since a month and I'm out of ideas.
I tried to resize the array to fit exactly the size of the matrix, I tried to preallocate a higher number of nonzeros space and lower and reallocate the matrices... nothing let the first matrix work.
Any help would be really highly appreciated...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I don't think that it is useful to ask about internal implementation details of MKL and other proprietary library routines without having good reasons for wanting to know. Even if you were able to elicit a reply with that information, you could not rely upon that information since it is not part of the specification for the interface. When the library is revised for a future release, the information may no longer be valid.
Among the arguments to Pardiso are these: n, a, ia, ja. Given these, the routine can obtain nnz = ia(n+1). It follows that MKL should only use ja(1:nnz) and a(1:nnz). It is crucial that ia(n+1) should contain the correct value.
How the vectors/matrices are allocated and initialized is of no consequence to Pardiso. The arrays may be statically or dynamically allocated. If the latter, whether the allocation was done by the Fortran runtime, mkl_malloc, calloc or malloc should have no effect on the results returned by Pardiso. The arrays may be filled from data in a file, or with values obtained from a prior calculation. Pardiso does not take array arguments whose allocation it should be able to change; it neither needs to nor should it be able to apply intrinsics such as UBOUND to the array arguments. Pardiso does not take optional arguments or arguments based on keywords.
The two matrices at the end are ABSOLUTELY IDENTICAL. It changes the way they're allocated first.
I presume that you meant to say that the behavior of Pardiso and/or the resulting solution are changed by the way the arrays are allocated. This is not the way things should be, nor do I think that this happens, based on having used Pardiso regularly for a number of years. I have called MKL/Pardiso from Fortran source files that I compiled with other compilers than Intel Fortran, and those programs would have failed if Pardiso depended on detailed information regarding how arguments given to it had been allocated.
If you want to resolve the bugs, you probably need to make up complete test codes that demonstrate what you claim. We have to establish that you are, indeed, calling Pardiso with matching array contents in the two cases. Until that is done, it makes little sense to try to find bugs based on the values supplied in IPARM.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
In the area of questions which you didn't really ask: if you are using a threaded MKL function for CSR, it likely divides the work among threads by scanning the sizes of the individual array sections and allocating a nearly equal total size to each thread (probably not by schedule dynamic). This would help maintain locality on a NUMA such as multiple CPU Xeon. Regardless of internal implementation, if you depend on a more strict ordering of data storage than what is required by the basic algorithm (which might not necessarily match the public open source), you are doing something wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi again,
In these days I had some time to inspect the code and make different runs. About that, I want to show you some interesting results.
I share with you two different matrixes in CSR3 format that are exactly the same. Except for a tiny difference... Which?
I exported the matrix (i.e. the 3 arrays) using std::scientific << std::setprecision(12)
and then with std::scientific << std::setprecision(24)
But... what happens to the results?
With 24digits precision I get a norm-2 of the residual of 3.95e+07 (yes, it's a plus)
with 12digits precision it drops at 3.2e-15.
As you notice, the lower the precision the better the results. You probably think that the matrix is ill-conditioned and such a difference in the precision of matrix coefficients matter, But the conditioning number of both the matrix is almost the same (around 3e+5) and other solvers (Mumps and Matlab) have never had problems finding the correct solution!
If I made any mistake setting the solver please notify me! I used almost default paramers.
Is there nothing I can do to solve this problem?
Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dario M. wrote:The zip file contains no code, so we know nothing about what settings you used, and what you mean by "almost default parameters".
If I made any mistake setting the solver please notify me! I used almost default paramers. Is there nothing I can do to solve this problem?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The "almost" is really almost. I changed only IPARM(35) to set zero-indexed arrays.
I also tried changing some settings: you can find them in the very first comment of this post.
There are two possibilities:
- my code is bugged. But I used Pardiso with many other problems and gives good results and also the same pardiso called with two slighty different matrices shouldn't give a so different result. However if you think that the problem is nested there I will try to rewrite some code for a plain Pardiso (since now the code it's written to work inside a bigger software).
- I didn't set IPARM or something like that in the good way. In this case if you already know the solution it would be really easy...
Let me know if I had to write some code or if you can run the matrix I provided on your machines without trouble simply importing the txt files into a C array.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There is an example code, pardiso_unsym_c.c, in the MKL distribution, in the directory .../mkl/examples/solverc/source. You can modify it to read the matrix data from your data files and compute and print the residuals. If you see the same behavior (very different norm of residual vector with a12.txt versus a24.txt), attach your modified code and a description of how the results differ, and then there will be something tangible for the MKL group to work with.
Pardiso calls are more complicated than calls to most BLAS and Lapack routines. In particular, given the need to hold a large matrix in CSC sparse matrix storage format, the IPARM array with numerous control parameters in it and the need to call Pardiso in a particular sequence, it is easy to see that there are more opportunities to make mistakes. However, the extra work and care needed to get all this right is well rewarded by the high performance of the Pardiso solver. MKL also provides the alternative DSS interface to Pardiso, which you may consider using as a less error-prone way of solving sparse equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I never tried the DSS interface but I will give it a look if you recommend it! Thank you for the hint
In the zip you'll find a slightly modified pardiso_unsym_c.c (called Source.cpp) that loads the data.
There are 3 #define:
MY_DATA 1: loads my matrices; 0:use the original values of pardiso_unsym_c.c
USE_ONE_INDEX 1: adapts my matrix to one-indexed matrices; 0:uses the original index and put IPARM(35)=1
USE_PRECISION24 1: loads the 24digits precision; 0: uses the 12digits precision (unuseful with MY_DATA=0)
On my machine I'll get a very strange result:
using zero-indices they'll both give errors of e+60 (never happened before)
however using one-indexed arrays I will have the behaviour that I'm used to see: with 24 I'll get e+6; with 12 I'll get e-8.
Thank you again for your efforts
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I think that you attached the same zip file that you posted in #6 again. There is no C/C++ source file in the zip file of #10.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Meanwhile I want to show you another interesting result.
- I took the simple pardiso_unsym_c.c
- I modified ia and ja to be zero-indexed (i.e. I subtracted 1 both to ia and ja)
- I set iparm[34] (for documentation iparm(35)) to 1 that means zero-indexed arrays
Now... what did I do so terrible that I have messed up everything? Now the relative residual looks like e+62 instead of e-16?
I think I'm missing something something, but I can't undestand what.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have noticed several odd features of your matrix. For example, it has a trailing diagonal block, rows 433:n and columns 433:n, which is completely zero. This property could be exploited to speed up the solution.
Next, your matrix is nearly singular -- Matlab gave me zero for the determinant, and the matrix is not full rank if you specify a tolerance of, say, 10-5. I have observed Pardiso giving different results compared to those from Matlab and Mumps, but I don't feel comfortable that what I have seen is all true and not the result of some mistake in the code or the manipulation of the matrix data. So, I ask: Is it possible for you to produce a smaller matrix that exhibits similar problems? For example, if your FEA program could be rerun with a coarser mesh, and the matrix dumped out as before? I realize that this is more work for you, but it may become possible to narrow down a bug in the library routine, or to confirm that your problem itself is pathological.
I suspect that your matrix is structurally symmetric, but I hesitate to make generalizations without looking at more matrices from your program. What do you think?
These comments are all based on posts #1 to #12; I have not yet looked at #13.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
About exploiting the diagonal zero block: what is the best way to handle the problem? Passing through Schur complement? Since I'll work with this kind of matrices it'll be very very helpful!
About the near-singularity: cutting with threshold at 1e-5=10^-5 is still not singular (for Matlab)! The conditioning number is exactly the same!
It does is singular when you cut at 1e-4, but honestly... for me 1e-4 is something! Moreover, if the problem was there, why with a matrix that has more or less the same conditioning number (and also less!!!), everything goes fine? A proof of that in the attachment. FYI, this new matrix comes from the same problem, just a few integration steps before.
I would think about data manipulation errors me too if my program would have relied always on data exchange through txt-based files. But originally Pardiso was called in the same program that produces the matrix, so no file exchange happen! And the problem was the same (as with 24precision). Said that, I don't know in how many other ways I could have "corrupted" datas, also because I would have corrupted in such a way that, exporting the arrays to Matlab everything works fine... Maybe I corrupted or mishandled something in the big main program that originally gave the error (in which arrays are handled through a custom CSR class), but importing raw data into a pure C array with very low level instructions into a Intel-provided example eliminates almost every possible source of error that I can think of.
It will be really hard for me to provide a smaller matrix with the same problems because the same kind of matrix, with the same size, that comes from the same problem, just few integration steps before... doesn't give this problems!!!
I didn't look carefully at the structure of the matrix because at this time the solver should be has generic as possible so I'm not leveraging on symmetries.
P.S. the new code has a #define called USE_WORKING_DATA 1:uses data from a matrix that works good (lower cond number, though) 0: uses data from the matrix that I already sent you in the previous post. In both cases you can select from 12 and 24 precision as before.
P.S. If you tried to run my code are you experiencing the same problems, with strange residuals and so on?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dario M. wrote:
P.S. If you tried to run my code are you experiencing the same problems, with strange residuals and so on?
Yes, I see strange residuals when I obtain a solution using MKL Pardiso, MKL/DSS, Pardiso-5. What is puzzling is that some of the solution components agree quite precisely with Matlab results, yet others disagree. Here, for example, are the numbers from Matlab (xs) and MKL/Pardiso (x) for the matrix of #12:
>> disp([xs(1:20) x(1:20)])
-4.718431735326641e-001 -4.718431735326600e-001
-5.023715842038469e-001 -5.023715842038500e-001
0 0
0 0
0 0
-3.320461241252870e+000 -3.320461241252900e+000
-8.723652569275131e-001 -8.723652569275100e-001
-2.317285637431159e+000 -2.317285637431200e+000
0 0
0 0
0 0
2.443606602800037e+000 2.443606602800000e+000
-6.484925942871733e-001 6.947416422904000e+001 <<=====
-8.167535398176279e-001 1.184012934578900e+002
0 0
I have solved the equations with MUMPS 4.10.0 an 5.0.1, with excellent results. For example:
Solved dario in 0.047 s Norm of residual = 7.661D-15 Largest residual = 3.997D-15
These numbers compare well with what I get from Matlab:
>> r=As*xs-b; norm(r)
ans =
5.115840582406517e-015
In contrast, Pardiso-5 gives
r( 18) = 3.728774D-01 r( 145) = 1.502216D+05 r( 146) = -8.812303D+04 r( 151) = -1.501766D+05 r( 152) = 8.815920D+04 Norm of residual = 2.463D+05
I suspect a bug somewhere, but I have failed to find it. This is the kind of situation where the job would be easier with a smaller matrix.
Do you have a description of the problem as it is before you discretize? For example, a verbal definition or a statement in terms of a PDE+initial and boundary conditions?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Oh, at least is not only my machine...
I've been able to reply the same problem with a smaller matrix (270 rows instead of 540).
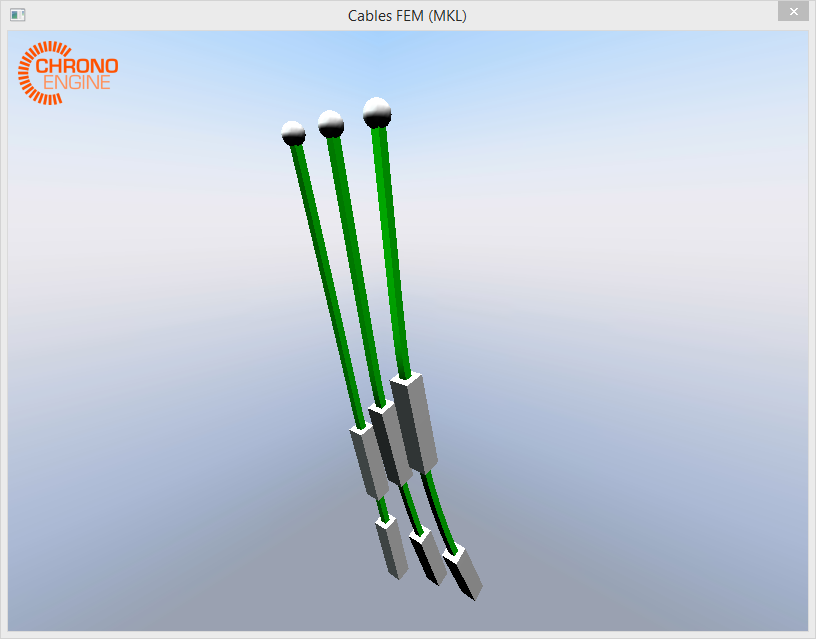
The simulation involves an arbitrary number of little chains made like this (very scientific notation):
o----------||||||||||--------------|||||||||||
o is a revolute joint; ------ is an finite element ANCF cable, not a simple beam; ||||||||| is a rigid body with its own mass.
There are 2 ANCF cables and 2 rigid bodies for each chain, but every chain has different ANCF cable length so there are different spacings between the different rigid bodies. A gravitational force is applied so they swing back and forth.
The problem arise when 3 or more of these chains are simulated together. No matter what is the length of the cables:
o--||||||||--------------------|||||||||| or o-----------|||||||||||-----------||||||||| give the same problem.
To let you better understand I took a screenshot.
In the attachment I provided some new (smaller) matrices with different "chain" length but that give the same problem. It might be useful having different matrices to test.
If you can suggest me how to effectively handle those matrices exploiting the zero diagonal block, I'd be really grateful!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dario, here are some observations to help you. Your matrices have many zero entries, and these zero entries do two bad things. A sparse matrix should not contain any, unless required as a placeholder (e.g., a diagonal element of a symmetric or structurally symmetric matrix). I removed the zero entries, and put your data into the following format (files with .CSR suffix):
Line-1: title Line-2: n,nnz,index base Lines 3 to n+2 : rowptr,rhs, i=1:n Lines n+3 to n+2+nnz : col(1:nnz),val(1:nnz)
I found that the removal of the zero-value matrix elements greatly improved the results from Pardiso. The residual norm remains at or below 10-7, and the solutions agree to six or more digits when the RHS values are switched from 12 to "24" digits. Note that double precision does not give you more than 16 digits of precision, even if you print out 24 digits.
The second issue is one that I am unable to address: a good fraction of the solution values are zero. Perhaps you can tell from your understanding of the physics which xi values should come out to zero, even before performing the solution. If so, you can eliminate the columns corresponding to those x values, and discard a number of equations equal in number to the count of zero-valued solutions.
For example, Beam35 has 270 unknowns and 3276 matrix entries. However, only 2497 of those entries are non-zero, and 105 of the 270 elements of the solution are zero.
The .CSR files and files with the solution vectors are in the attached zip file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Line-1: title Line-2: n,nnz,index base Lines 3 to n+2 : rowptr,rhs, i=1:n Lines n+3 to n+2+nnz : col(1:nnz),val(1:nnz)
My data save in .CSR file as above format. How I can store this data into ia, ja, a in c++ for pardiso solution call?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks mecej4 for your help! Now the simulation runs fine!
I will give an in-depth look at the problem to exploit some other features of these matrices.
Meanwhile can you suggest me a smart way to handle saddle-point problems? In the cookbook I can't find any recipe that could fit my case.
Thank you again for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I am glad that the work-around (removing matrix elements that are zero) helped, but it is troubling that Pardiso (and not one of the four other solvers that I tried) seems to have a problem with your matrices, generating unexpectedly huge residuals. The underlying issue needs to be investigated and fixed, but it may be difficult to convince the author (Dr. Schenk) that there is a problem, without being able to provide a small test matrix with that property. Please keep this in mind, and if you find yourself with a small matrix with similar problems in the future, please report it.
I should like to know: do you know which x-values may turn out to be zero before solving the simultaneous equations?
I do not know what you mean by "saddle-point problems". Please elaborate.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page