Fast Discrete Fourier Transform with MKL

[Harry_G_]

Hi all,

In R programming, there is the "fft" function: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/fft.html

> x <- c(102, 55, 89, 12, 3, 45, 9)
> fft(x)
[1] 315.00000+ 0.00000i  98.57101-82.76603i -23.61882-18.71932i
[4] 124.54781+ 5.66758i 124.54781- 5.66758i -23.61882+18.71932i
[7]  98.57101+82.76603i
> Re(fft(x))
[1] 315.00000  98.57101 -23.61882 124.54781 124.54781 -23.61882  98.57101

What I have to is to replicate the Re(fft(x)) output in Fortran. I wonder if Intel MKL could do the job.

! testfft.f90

program myfft

 implicit none
 integer, dimension(7) :: x
 double precision, dimension(7) :: Refftx

 x = (/ 102, 55, 89, 12, 3, 45, 9 /)

 ! ============================================================ ! 
 ! Here, I need to use a fft function to return the result in R !
 ! ============================================================ ! 
 
 ! For example, 
 
 Refftx = theFFTfunctionIdonotKnow(x)

 print*, Refftx

end program myfft

How do I have to build/compile the "testfft.f90" file?

The machine I use is equipped with Intel Parallel Studio XE 2013. I generally compile .f90 files by typing ifort myfile.f90 on the Intel 64 Visual Studio 2008 mode command prompt. The machine runs Window 7 64 bit.

Thank you very much!

[Ying_H_Intel]

Hi Harry, 

As i understand, your question may include several subquestions

1) first ,  replicate the Re(fft(x)) output in Fortran using MKL function

The step is not complex. MKL provide example code (both c and fortran code) in MKL install directory, for example, dftf\source\basic_dp_real_dft_1d.f90. 

And the sample also include compile and link command, you can follow the setting to build the code. 

simply, it is   >ifort mkl_dfti.f90, basic_dp_real_dft_1d.f90 -mkl 

I change the code of   basic_dp_real_dft_1d.f90.

print *,"Initialize data for real-to-complex FFT"

!  call init_r(x_real, N, H)
  x_real = (/ 102, 55, 89, 12, 3, 45, 9 /)
  print *, x_real

  print *,"Compute forward transform"
  status = DftiComputeForward(hand, x_real, x_cmplx)
  if (0 /= status) goto 999

  print *,"Verify the result"
  print *, x_cmplx
    print *, Real(x_cmplx)

Then you will see the result ( CCE storage).  and  how to call MKL function to implement the FFT computation. 

2) second questions, integrate MKL to R environment. 

we have two usage model: 

1. build R with MKL,   it will use MKL blas and Lapack funtion 

2   If you want to use MKL FFT in R,  there may some ways,  the below is one of  them we had tried. 

Writing R extensions with MKL. 

–R manuals: Writing R extensions
http://cran.r-project.org/doc/manuals/r-release/R-exts.html

–KB article: Extending R with Intel® MKL
http://software.intel.com/en-us/articles/extending-r-with-intel-mkl

It is c language, but it should be same with Fortran language.  

Hope it helps and please share if you have any progress 

Best Regards,

Ying

[Harry_G_]

<Question section 1:>

I can modify the basic_dp_real_dft_1d.f90 file here in C:\Program Files (x86)\Intel\Composer XE 2013\mkl\examples\dftf\source, as you suggested. Also, I noticed that the mkl_dfti.f90 file is located in C:\Program Files (x86)\Intel\Composer XE 2013\mkl\include. And the Command Prompt looks like:

 

Now, (1) which folder do I have to move to? (2) Then, is it the command > ifort mkl_dfti.f90, basic_dp_real_dft_1d.f90 -mkl , including a comma between the two .f90 files ? Or, do I have to copy the two files to my working folder and ifort there?

<Question section 2:>

I have a bunch of tasks before calculating the Re(fft(x)). Isn't there a way to retain my existing main.f90 code and call the FFT operation from the main.f90.

EDIT:

I have an update for the <Question section 1>. I happened to find https://software.intel.com/en-us/forums/topic/336695. The author used /Qmkl. I don't know what the heck is /Qmkl. The /mkl alone without the Q did not work. Anyway, the ifort command goes like:

>ifort "C:\Program Files (x86)\Intel\Composer XE 2013\mkl\include\mkl_dfti.f90" dft1d.f90 -o dft1d /Qmkl

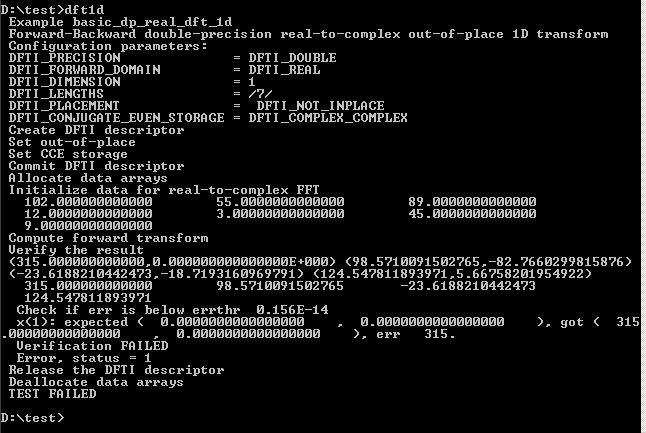
The above is to replicate Re(fft(c(102,55,89,12,3,45,9,9,55))) in R. Something seemingly goes wrong. I attach the dft1d.f90 file, hoping someone is out there who is interested in this problem.

Thank you.

[Ying_H_Intel]

Hi Harry, 

Right, you can copy the example code to your work folder and compile it with /Qmkl option. ( it is compiler option) 

And the FFT result you are seeing is stored by CCE format.   You may see the details in MKL manual =>

DFTI_CONJUGATE_EVEN_STORAGE: storage scheme for a conjugate-even domain
The Intel MKL FFT interface supports two configuration values for this parameter: 

Then just complete the result. 

Best Regards,

Ying

[Dmitry_B_Intel]

Harry,

That 'Verification of result' failed after you modified the example is no worry. Verifier checks the output of the transform assuming the input was specially crafted. Since you give your own input, the verifier complaints.

Unlike R, in Fortran the result contains only a half of full data, because the other half can be easily restored by conjugate-even symmetry of the result (follow Ying's note for details).

Thanks
Dima

[Ying_H_Intel]

Hi Harry, 

Just complete the thread,

after get  FFT result  which is CCE format, then use the below code to get the whole output or Re(z).  please see  MKL  manual => chapter 12  =>  DFTI_CONJUGATE_EVEN_STORAGE: storage scheme for a conjugate-even domain.

The following examples illustrate usage of the DFTI_COMPLEX_COMPLEXstorage for a conjugate-even
domain:
! Fortran
real :: AR(N1,N2,M) ! Array containing values of R
complex :: AZ(N1/2+1,N2,M) ! Array containing values of Z
...
! on input: R{k1,k2,m} = AR(k1,k2,m)
status = DftiComputeForward( desc, AR(:,1,1), AZ(:,1,1) )
! on output:
! for k1=1 … N1/2+1: Z{k1,k2,m} = AZ(k1,k2,m)
! for k1=N1/2+2 … N1: Z{k1,k2,m} = conj(AZ(mod(N1-k1+1,N1)+1,mod(N2-k2+1,N2)+1,m))
// C/C++
float *AR = malloc( N1*N2*M * sizeof(AR[0]) );
complex *AZ = malloc( N1*(N2/2+1)*M * sizeof(AZ[0]) );
MKL_LONG is[3], os[3], idist, odist; // input and output strides and distance
...
// on input: R{k1,k2,m} 
// = AR[is[0] + k1*is[1] + k2*is[2] + m*idist]
status = DftiComputeForward( desc, R, C );
// on output:
// for k2=0…N2/2: Z{k1,k2,m} = AZ[os[0]+k1*os[1]+k2*os[2]+m*odist]
// for k2=N2/2+1…N2-1: Z{k1,k2,m} = conj(AZ[os[0]+(N1-k1)%N1*os[1]
// +(N2-k2)%N2*os[2]+m*odist])

Dima give one example to convert the general input to CCE formart as below.,  you may do the inverse operation. 

Best Regards,

Ying