- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
I am trying to use PARDISO for solving a structurally symmetric complex matrix generated by a FEM scheme, and I am quite confused by its memory requirements.
When running PARDISO with a 144k equations matrix, I see a memory consumption up to 3GB in the factorization step. If I disable the permutation, by setting perm[i]=i in the perm array and iparm[4] = 1, it goes up to 5GB (I will use C++ 0-based indexing in this post as to avoid confusion).
I find this behavior to be a bit surprising, given that for symmetric real problems I normally see a negligible memory consumption for matrices around the same size.
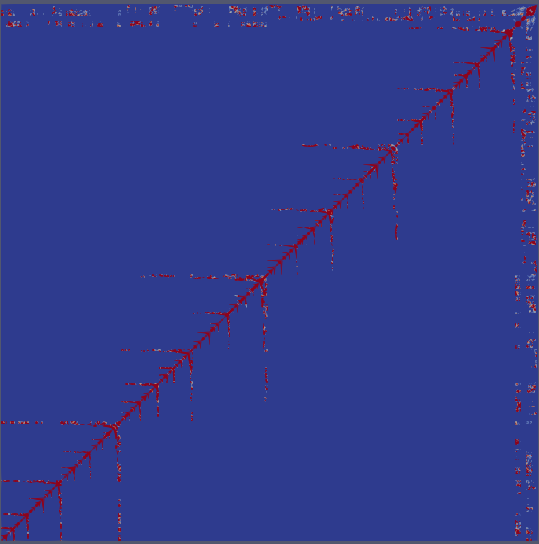
Attached you can see the sparsity pattern of the input matrix
with the red color denoting non-zero positions (each block actually corresponds to ~15 equations).
With iparm[4] = 2 I was able to inspect the matrix after PARDISO's reordering, and its sparsity pattern is as follows
Is this memory consumption considered normal? This matrix is obtained from a really coarse mesh, so for any practical application I wouldn't be able to use PARDISO if that is the case (perhaps with OOC mode, with I wouldn't expected to be needed for systems this big).
I first had this results using 32bit interface of oneAPI MKL 2021, and I didn't get any different results by using the 64bit interface of both 2021 and 2023 MKLs. All the tests were performed in a C++ code compiled with gcc in a Linux environment.
Unfortunately I cannot post here an easy way to generate such results, as it would require to download and compile a C++ library.
If there is further information that I could provide in order to provide more insight to this problem, I would be really happy to do so.
Thank you in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Francisco,
Is this memory consumption considered normal?
>>In general if X Gbytes memory is needed to solve a particular problem in core.
The amount of memory for In-Core mode can be roughly represented as a sum of (permanent memory on phase 11) + (peak memory on phases 22 and 33) = M11 + M_incore_23 = iparm[15] + iparm[16] = M_ic , while the OOC memory is estimated as (permanent memory on phase 11) + (memory required for the ooc-specific part) = M11 + M_ooc_23 = iparm[15] + iparm[62] = M_ooc
The ratio between In-Core and OOC modes is pretty small in some cases.
Please find the below link for more information regarding OOC below.
https://www.intel.com/content/www/us/en/developer/articles/training/how-to-use-ooc-pardiso.html
From the number of non-zeros in L+U: 151449993, if considering double complex data here, then non-zeros data size is 151449993*8*2 ~= 2.5GB, so using 3GB for the shared sample reproducer looks reasonable and seems not an issue.
Best Regards,
Shanmukh.SS
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello again,
I've isolated the program in a simple .cpp file that will read the matrix in CSR format from a text file.
In this Google Drive folder you will find the relevant text files and the cpp source code, and below the PARDISO output.
Please, let me know if there is any further information that I could provide.
All the best,
Francisco Orlandini
=== PARDISO is running in In-Core mode, because iparam(60)=0 ===
Percentage of computed non-zeros for LL^T factorization
1 % 2 % 3 % 4 % 5 % 6 % 7 % 8 % 9 % 10 % 11 % 12 % 13 % 14 % 15 % 16 % 17 % 18 % 19 % 20 % 21 % 22 % 23 % 24 % 25 % 26 % 27 % 28 % 29 % 30 % 31 % 32 % 33 % 34 % 35 % 36 % 37 % 38 % 39 % 40 % 41 % 42 % 43 % 44 % 45 % 47 % 48 % 49 % 51 % 52 % 53 % 54 % 55 % 56 % 57 % 58 % 59 % 61 % 62 % 63 % 64 % 65 % 67 % 69 % 71 % 73 % 75 % 77 % 78 % 79 % 80 % 81 % 82 % 85 % 88 % 90 % 92 % 93 % 95 % 96 % 97 % 98 % 99 % 100 %
=== PARDISO: solving a complex structurally symmetric system ===
Matrix checker is turned ON
0-based array is turned ON
PARDISO double precision computation is turned ON
METIS algorithm at reorder step is turned ON
Single-level factorization algorithm is turned ON
Summary: ( starting phase is reordering, ending phase is factorization )
================
Times:
======
Time spent in calculations of symmetric matrix portrait (fulladj): 0.038899 s
Time spent in reordering of the initial matrix (reorder) : 0.719669 s
Time spent in symbolic factorization (symbfct) : 0.164026 s
Time spent in data preparations for factorization (parlist) : 0.004884 s
Time spent in copying matrix to internal data structure (A to LU): 0.000000 s
Time spent in factorization step (numfct) : 15.284947 s
Time spent in allocation of internal data structures (malloc) : 0.024751 s
Time spent in additional calculations : 0.305008 s
Total time spent : 16.542184 s
Statistics:
===========
Parallel Direct Factorization is running on 6 OpenMP
< Linear system Ax = b >
number of equations: 144657
number of non-zeros in A: 8811657
number of non-zeros in A (%): 0.042109
number of right-hand sides: 1
< Factors L and U >
number of columns for each panel: 72
number of independent subgraphs: 0
< Preprocessing with state of the art partitioning metis>
number of supernodes: 16666
size of largest supernode: 4251
number of non-zeros in L: 77945805
number of non-zeros in U: 73504188
number of non-zeros in L+U: 151449993
gflop for the numerical factorization: 1100.816559
gflop/s for the numerical factorization: 72.019651
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello again,
I have managed to isolate the problem in a single .cpp file and three text files containing the matrix in the CSR format.
The files can be obtained in this Google Drive link , and below one can see PARDISO's output.
Best regards,
Francisco
=== PARDISO is running in In-Core mode, because iparam(60)=0 ===
Percentage of computed non-zeros for LL^T factorization
1 % 2 % 3 % 4 % 5 % 6 % 7 % 8 % 9 % 10 % 11 % 12 % 13 % 14 % 15 % 16 % 17 % 18 % 19 % 20 % 21 % 22 % 23 % 24 % 25 % 26 % 27 % 28 % 29 % 30 % 31 % 32 % 33 % 34 % 35 % 36 % 37 % 38 % 39 % 40 % 41 % 42 % 43 % 44 % 45 % 47 % 48 % 49 % 51 % 52 % 53 % 54 % 55 % 56 % 57 % 58 % 59 % 61 % 62 % 63 % 64 % 65 % 67 % 69 % 71 % 73 % 75 % 77 % 78 % 79 % 80 % 81 % 82 % 85 % 88 % 90 % 92 % 93 % 95 % 96 % 97 % 98 % 99 % 100 %
=== PARDISO: solving a complex structurally symmetric system ===
Matrix checker is turned ON
0-based array is turned ON
PARDISO double precision computation is turned ON
METIS algorithm at reorder step is turned ON
Single-level factorization algorithm is turned ON
Summary: ( starting phase is reordering, ending phase is factorization )
================
Times:
======
Time spent in calculations of symmetric matrix portrait (fulladj): 0.038899 s
Time spent in reordering of the initial matrix (reorder) : 0.719669 s
Time spent in symbolic factorization (symbfct) : 0.164026 s
Time spent in data preparations for factorization (parlist) : 0.004884 s
Time spent in copying matrix to internal data structure (A to LU): 0.000000 s
Time spent in factorization step (numfct) : 15.284947 s
Time spent in allocation of internal data structures (malloc) : 0.024751 s
Time spent in additional calculations : 0.305008 s
Total time spent : 16.542184 s
Statistics:
===========
Parallel Direct Factorization is running on 6 OpenMP
< Linear system Ax = b >
number of equations: 144657
number of non-zeros in A: 8811657
number of non-zeros in A (%): 0.042109
number of right-hand sides: 1
< Factors L and U >
number of columns for each panel: 72
number of independent subgraphs: 0
< Preprocessing with state of the art partitioning metis>
number of supernodes: 16666
size of largest supernode: 4251
number of non-zeros in L: 77945805
number of non-zeros in U: 73504188
number of non-zeros in L+U: 151449993
gflop for the numerical factorization: 1100.816559
gflop/s for the numerical factorization: 72.019651
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello again,
I have managed to isolate the problem in a single .cpp file and three text files containing the matrix in the CSR format.
The files can be obtained in this Google Drive link , and below one can see PARDISO's output.
Best regards,
Francisco
=== PARDISO is running in In-Core mode, because iparam(60)=0 ===
Percentage of computed non-zeros for LL^T factorization
1 % 2 % 3 % 4 % 5 % 6 % 7 % 8 % 9 % 10 % 11 % 12 % 13 % 14 % 15 % 16 % 17 % 18 % 19 % 20 % 21 % 22 % 23 % 24 % 25 % 26 % 27 % 28 % 29 % 30 % 31 % 32 % 33 % 34 % 35 % 36 % 37 % 38 % 39 % 40 % 41 % 42 % 43 % 44 % 45 % 47 % 48 % 49 % 51 % 52 % 53 % 54 % 55 % 56 % 57 % 58 % 59 % 61 % 62 % 63 % 64 % 65 % 67 % 69 % 71 % 73 % 75 % 77 % 78 % 79 % 80 % 81 % 82 % 85 % 88 % 90 % 92 % 93 % 95 % 96 % 97 % 98 % 99 % 100 %
=== PARDISO: solving a complex structurally symmetric system ===
Matrix checker is turned ON
0-based array is turned ON
PARDISO double precision computation is turned ON
METIS algorithm at reorder step is turned ON
Single-level factorization algorithm is turned ON
Summary: ( starting phase is reordering, ending phase is factorization )
================
Times:
======
Time spent in calculations of symmetric matrix portrait (fulladj): 0.038899 s
Time spent in reordering of the initial matrix (reorder) : 0.719669 s
Time spent in symbolic factorization (symbfct) : 0.164026 s
Time spent in data preparations for factorization (parlist) : 0.004884 s
Time spent in copying matrix to internal data structure (A to LU): 0.000000 s
Time spent in factorization step (numfct) : 15.284947 s
Time spent in allocation of internal data structures (malloc) : 0.024751 s
Time spent in additional calculations : 0.305008 s
Total time spent : 16.542184 s
Statistics:
===========
Parallel Direct Factorization is running on 6 OpenMP
< Linear system Ax = b >
number of equations: 144657
number of non-zeros in A: 8811657
number of non-zeros in A (%): 0.042109
number of right-hand sides: 1
< Factors L and U >
number of columns for each panel: 72
number of independent subgraphs: 0
< Preprocessing with state of the art partitioning metis>
number of supernodes: 16666
size of largest supernode: 4251
number of non-zeros in L: 77945805
number of non-zeros in U: 73504188
number of non-zeros in L+U: 151449993
gflop for the numerical factorization: 1100.816559
gflop/s for the numerical factorization: 72.019651
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Francisco,
Thanks for posting on Intel Communities.
We are looking into the mentioned details. We tried compiling the shared source code. However, we are facing issues while compiling the same. Could you please confirm if the parameters passed to pardiso_64 were of the correct type? It seems there is a type conversion issue with the parameters.
Best Regards,
Shanmukh.SS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello Shanmukh.SS,
the code as provided would run with the `-DMKL_ILP64` compiler directive.
I've updated the code as to run with both LP64 and ILP64 interfaces. Would you please check if it compiles on your machine?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Francisco.
I've updated the code as to run with both LP64 and ILP64 interfaces. Would you please check if it compiles on your machine?
>>Thanks for sharing the details. We have compiled the shared source code and we were able to run it successfully. We are discussing your issue internally. We will get back to you with an update soon!
Best Regards,
Shanmukh.SS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Francisco,
Is this memory consumption considered normal?
>>In general if X Gbytes memory is needed to solve a particular problem in core.
The amount of memory for In-Core mode can be roughly represented as a sum of (permanent memory on phase 11) + (peak memory on phases 22 and 33) = M11 + M_incore_23 = iparm[15] + iparm[16] = M_ic , while the OOC memory is estimated as (permanent memory on phase 11) + (memory required for the ooc-specific part) = M11 + M_ooc_23 = iparm[15] + iparm[62] = M_ooc
The ratio between In-Core and OOC modes is pretty small in some cases.
Please find the below link for more information regarding OOC below.
https://www.intel.com/content/www/us/en/developer/articles/training/how-to-use-ooc-pardiso.html
From the number of non-zeros in L+U: 151449993, if considering double complex data here, then non-zeros data size is 151449993*8*2 ~= 2.5GB, so using 3GB for the shared sample reproducer looks reasonable and seems not an issue.
Best Regards,
Shanmukh.SS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dear @ShanmukhS_Intel ,
I do agree that considering the number of non-zeros in L+U, the memory consumption seems quite reasonable. Comparing with some other examples I was able to generate, I think that there is an issue with the connectivity of my matrix. The amount and size of supernodes are quite different from other examples.
Thank you very much for your response.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@FranciscoOrlandinii wrote:
Hello again,
I have managed to isolate the problem in a single .cpp file and three text files containing the matrix in the CSR format.
The files can be obtained in this Google Drive link , and below one can see PARDISO's output.
Best regards,
Francisco
Sorry, but i could not open the Google Drive link.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dear @xibalba22 ,
I've managed to open the link in an anonymous tab with no issues, so I am not sure why weren't you able to do so.
However, given @ShanmukhS_Intel , unless you are really curious, I don't think that it's worth further investigation on this issue. Thank you very much for your interest.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Francisco,
If this resolves your issue, make sure to accept this as a solution. This would help others with a similar issue. Thank you!
Have a great day!
Best Regards,
Shanmukh.SS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Francisco,
Thanks for accepting our solution. If you need any additional information, please post a new question as this thread will no longer be monitored by Intel.
Best Regards,
Shanmukh.SS
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page