- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
I am performing a sparse matrix vector multiplication and thought it might be beneficial to reduce the bandwidth of the matrix, such that fewer loading operations must be performed. I implemented the bandwidth compression via similarity transformation that uses the permutation matrices generated through the Cuthill McKee algorithm from the boost library.
Since I use this for a simulation and it is long time stable, I can be pretty sure that the transformation works as it is supposed to do. But the scalability is a little bit puzzling.
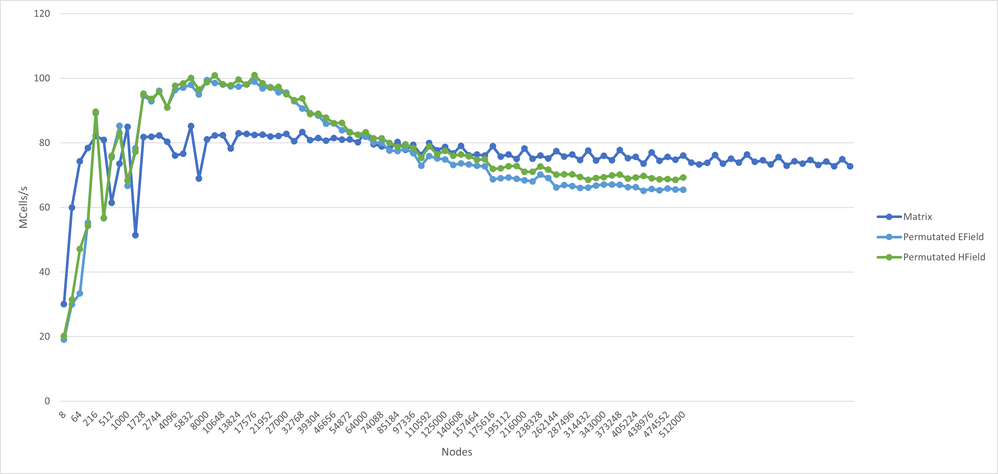
The dark blue curve (Matrix) shows the scalability without bandwidth compression. The other two curves display the behaviour after a bandwidth compression. As you can see it is initially beneficial but drops below the original performance from a certain point.
Is there maybe already something bandwidth related implemented in the sparse matrix-vector operations, that might interfere with my algorithm?
Regards,
Jan
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There are many factors that can affect the speed of a sparse matrix - vector multiplication, of which bandwidth is just one.
For example, what happens to the count of non-zero matrix elements within the band? Reordering to minimize the bandwidth can cause that count to go up.
Are your timing results from a single-threaded program or are you using the multithreaded version of the MKL library?
What is the cache sizes of the machine and how well are the caches used?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I am linking the sequential MKL library to keep it simple for starters.
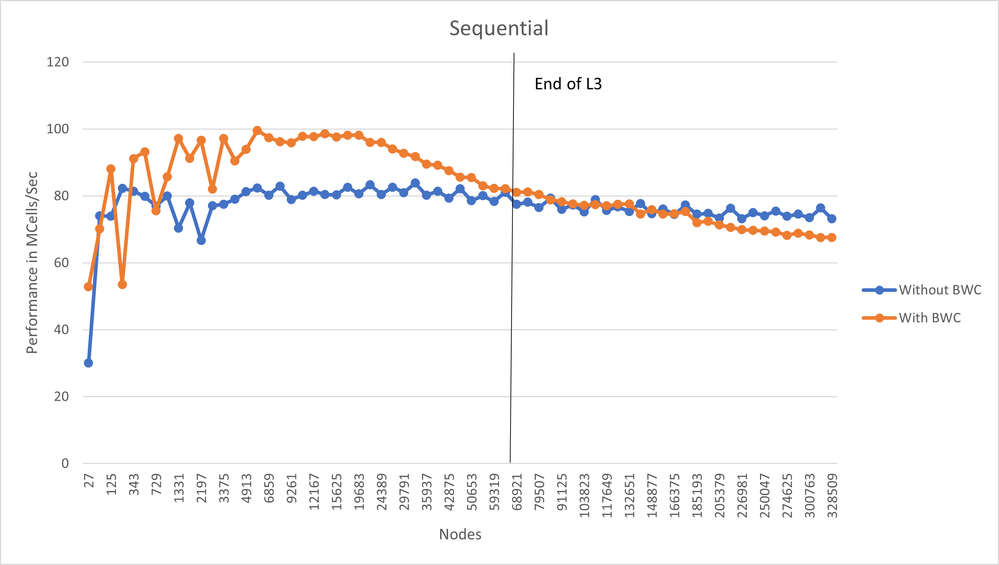
My PC contains a I7 6700K processor with 8 MB L3 Cache. The floating point NNZ which I have to store are 30 * N (N = Nodes, which are updated in each iteration). Times 4 Bytes (single precision), we can expect, that the L3 runs out at around 66 666 Nodes, which is about the area where all the lines touch.
Since the BW compression should make the multiplication more cache friendly (since NNZ are closer together) it makes sense that I gain a performance peak if the Cache is sufficient. I just wander about
- The performance drop when it becomes memory bound (After 66 666 Nodes)
- That the difference between HField and EField curves is so small. Both are calculated in separate equations and both their matrices are using the same permutation matrix for BW compression. Thus only one of the matrices actually gets a smaller BW (0.00.. of the original BW) and the other even gets an increased BW (1. something). But the difference between both curves is just about ~5MCells/sec
Since the original curve (Matrix curve) is constant I assume that MKL uses some kind of blocking strategy internally. Can it be that there is something implemented that does not work nicely together with my BW compression and causes the drop below the matrix curve?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello Jan!
I strongly advise against analyzing bandwidth in a single-core run. The reason is that single core memory bound application is limited by completely different factors than multi-threaded memory bound application.
Proof: run STREAM Triad on a single core and on all cores. You'll notice non-matching numbers. The reason would be that single core performance is concurrency/latency limited (which often boils down to the number of LFB = number of outstanding requests which can be in the fly) whereas full machine run will be bound by the memory bandwidth (~ memory characteristics + # channels). I'm more confident in saying that when I talk about servers, for clients I have done much fewer experiments (so if you target client CPUs, let us know).
So, before trying to give any more specific advice, I'd like to ask: is it really the single core performance which you care about? if not, I suggest to modify your benchmark (you can still link to sequential MKL, but run same computation on multiple cores (say, through MPI or by any other means)).
Also, do you call mkl_sparse_optimize with hints for matrix-vector product? As another check, if you suspect MKL is doing something bad, you can right a default CSR MV kernel in C (since it is sequential run, for a bandwidth-reduced matrix you'll get a decent performance from that kernel already, although might not achieve the best performance possible). I suspect that you will get the same charts qualitatively.
Best,
Kirill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Yes, I use the mkl_sparse_set_mv_hint and mkl_sparse_optimize methods.
I am interested in knowing if and to what extent bandwidth compression would give me a performance advantage. I use a sequential code, as it means that I have to consider fewer influences and can eliminate possible sources of error. My assumption for matrix-vector multiplication is: The accesses to the vector entries are closer together if the associated matrix has a small bandwidth. Thus, I get fewer cache misses whether I use multiple cores or just one.
My algorithm consists of two steps: matrix construction and iterative matrix-vector multiplication.
In the first stage, I create my CSR matrix in a particular form (consisting of multiple bands that may be interrupted at certain rows) and compute the permutation vector using the Boost library. Then I perform the similarity transformation on my matrix C with the permutation matrix P: Cnew = P * C P^T. This transformation gives the correct result and is repeatable.
In the second stage, I repeatedly calculate e = C * h + e (e and h are vectors), or e = Cnew * h + e.
For my first curve (the dark blue one, named Matrix), I did not use the similarity transformation and simply used the matrix C in my matrix-vector calculations. For the other two curves, I used Cnew. I am comparing the performance of these two calculations, not the performance of the bandwidth analysis/compression. The times of the setup phase are not considered in this performance analysis. You could say, I am investigating the influence of the shape of a matrix on the performance of a matrix-vector multiplication.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi again!
So, to my knowledge, the effect of bandwidth reduction should only have positive effect on performance, at least when we talk about memory bandwidth bound regimes (multicore). And I don't see a good reason why internal MKL optimizations would negatively interfere with the bandwidth reduction for matrix-vector operation.
1) I suggest than you share your reproducer if possible so that we can check what happens on our side. For starters we would only need a case where you see a stable difference for a single matrix, with and without permutation. So we'd need ~ the calling code (to see how/whether you do warmup, how you allocate the data and call MKL etc), permuted and non-permuted matrices.
Also, please share the SW/HW details (OS, version of MKL, how many cores, how you set thread affinity, numactl, etc.).
2) second suggestion (repeating my previous post): conclusions from sequential case does not translate to multi-threaded case because different HW effects (LFB/mem latency for single core vs memory bandwidth for multi-core) limit performance.
Best,
Kirill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi again and sorry for the delay,
please find attached my reduced code for generating the matrices, performing the bandwidth reduction and matrix-vector multiplication. I am running the code on a PC with an Intel I7 6700k prozessor, 2x 8 GB RAM with Windows 10 as OS and I use Visual Studio 2017 as IDE. I don't do anything regarding numa or thread affinity. I set the thread amount to 4 and allignment of all vectors to 256, since this is advised for AX2 and my processor is capable of it. I thought mkl might use intrinsics below the hood. The boost library version is 1.76.0 and the version of MKL is 2021.2.0.
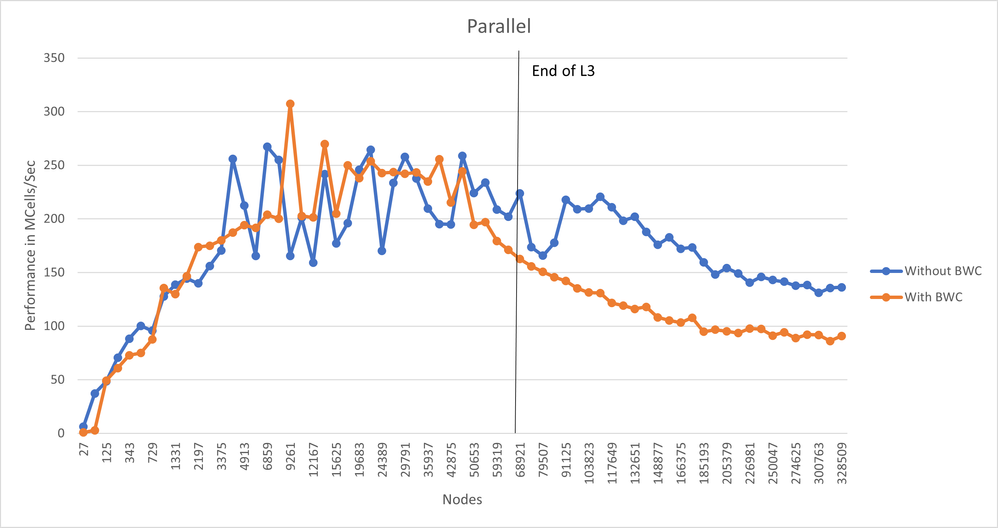
Since you proposed that the effect might show in parallel execution, I also investigated this case by changing the linked MKL library from Sequential to Parallel. The shown below are created with the measurements done by the attached code. It is visuable that bandwidth compression has a negative impact on the operation, even if the parallel mkl library is linked.
Kind regards,
Jan
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page