Intel® oneAPI Math Kernel Library
Ask questions and share information with other developers who use Intel® Math Kernel Library.
Announcements
The Intel sign-in experience has changed to support enhanced security controls. If you sign in, click here for more information.
6741 Discussions

mkl_sparse_sypr for symmetric (Non-Hermitian) complex matrices

Razmo86
Beginner
‎08-18-2021 11:46 AM
835 Views

 

Hello, 

 

I need to compute the symmetric product of three sparse matrices (D=P'AP) using the mkl_sparse_sypr routine, however I am not able to get the correct results. In my case, the P matrix is a general type real matrix, and the matrix A is a symmetric complex matrix. For example, consider the below matrices and their corresponding 3-array CSR format (for matrix A only the upper triangle is stored): 


Razmo86_0-1629308047024.png

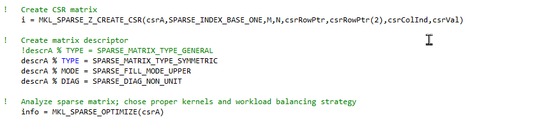
For matrix A, I created the CSR matrix and its descriptor as shown below: 

Razmo86_1-1629311055364.png

Similarly, for matrix P, it is defined as a general type matrix. Here I declared the REAL matrix P as a complex matrix ( the imaginary part of all the nonzero entries are set to zero): 

Razmo86_2-1629311146284.png

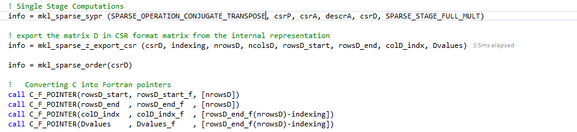
Finally, the below code is used to perform the symmetric product in a single computation stage. I also export the CSR results in order to validate the entries of the resultant symmetric matrix D.

Razmo86_3-1629311625731.png

The resultant matrix D has a correct sparsity pattern, however, in this example, two entries doesn't have a correct value (see highlighted below). The correct values are -4+12i and 2+12i, respectively. 

Razmo86_4-1629311991021.png

I observed the same issue once I tried to compute the PAP' using the SPARSE_OPERATION_NON_TRANSPOSE operation. The results appear to be correct for the cases where both A and P matrices are real. 

Is mkl_sparse_sypr routine only applicable to Hermitian complex  matrix A ?  Can it be applied to symmetric complex matrix A? 

Thanks   

 

0 Kudos

Link Copied

8 Replies
Gennady_F_Intel
Moderator
‎08-18-2021 09:12 PM
798 Views

This routine (C:=A*B*opA(A) ) is applicable if A has a general structure, B and C are symmetric or Hermitian matrices.  We don't know the issue wrt this routine in the current version of MKL. if you observe some problem - I would recommend give us the reproducer which we could compile and run on our end.

0 Kudos
Copy link
Razmo86
Beginner
‎08-19-2021 05:05 AM
756 Views
In response to Gennady_F_Intel

@Gennady_F_Intel  Thank you for looking into this issue. 


    

!============================================================================

!
! Consider the matrix A 
!
!                 |   1       -1+3i   0   -3+6i  0   |
!                 |  -1+3i     5      0    0     8   |
!   A    =        |   0        0      4    6     4   |,
!                 |  -3+6i     0      6    7     0   |
!                 |   0        8      4    0    -5   |
!
!  The matrix A is represented in a one-based compressed sparse row (CSR) storage
!  scheme with three arrays: Only the upper triangular part is stored
!
!         values  = ( 1 -1+3i -3+6i 5 8 4 6 4 7 -5 )
!         columns = ( 1 2 4 2 5 3 4 5 4 5 )
!         rowIndex = ( 1 4 6 9 10 11 )
!
!                 |   1        0      0       1      0   |
!                 |   0        0      4       0      0   |
!   P    =        |   0.5      0      0       0      0   |,
!                 |   0        0      0       1      0   |
!                 |   0     -6.5      0       0      1   |
!        
!         values  = ( 1 1 4 0.5 1 -6.5 1 )
!         columns = ( 1 4 3 1 4 2 5 )
!         rowIndex = ( 1 3 4 5 6 8 )   

!  The test performs the following operations :

    
!  The test performs the following operation :
!
!  The code computes D = P'AP using mkl_sparse_sypr. P is a MXM General 
  sparse matrix
!       where A is a symmetric sparse matrix where only the upper triangular part is stored
!
    
!*******************************************************************************
PROGRAM TestSPBLASProgram

    USE MKL_SPBLAS
    USE ISO_C_BINDING
    IMPLICIT NONE

    INTEGER M, N, NNZ,NNZP, i, info,j
!   *****************************************************************************
!   Sparse representation of the matrix A and P
!   *****************************************************************************
    INTEGER, ALLOCATABLE :: csrColInd(:), csrRowPtr(:),csrPColInd(:), csrPRowPtr(:)
    COMPLEX*16, ALLOCATABLE :: csrVal(:),csrPVal(:)

!   Matrix descriptor
    TYPE(MATRIX_DESCR) descrA,descrP,descrD     ! Sparse matrix descriptor
!   CSR matrix representation 
    TYPE(SPARSE_MATRIX_T) csrA,csrP,csrD        ! Structure with sparse matrix
!   *****************************************************************************
!   Declaration of local variables:
!   *****************************************************************************
 
    INTEGER :: nCol,nrowsD, ncolsD
    
    INTEGER(C_INT) :: indexing
    TYPE(C_PTR)    :: rowsD_start, rowsD_end, colD_indx, Dvalues
    
    INTEGER   , POINTER :: rowsD_start_f(:), rowsD_end_f(:), colD_indx_f(:)
    COMPLEX*16, POINTER :: Dvalues_f(:)
    
    

    NNZ = 10
    ALLOCATE(csrColInd(NNZ))
    ALLOCATE(csrRowPtr(M+1))
    ALLOCATE(csrVal(NNZ))
    
    csrVal = (/(1.0D0,0.0D0), (-1.0D0,3.0D0) ,(-3.0D0,6.0D0), (5.0D0,0.0D0) ,(8.0D0,0.0D0) ,(4.0D0,0.0D0) ,(6.0D0,0.0D0), (4.0D0,0.0D0), (7.0D0,0.0D0), (-5.0D0,0.0D0)/)
    csrColInd = (/ 1, 2, 4, 2, 5, 3, 4, 5, 4, 5 /)
    csrRowPtr = (/1, 4, 6, 9, 10, 11/)
    
    
    
    M = 5
    N = 5
    NNZP = 6
    ALLOCATE(csrPColInd(NNZP))
    ALLOCATE(csrPRowPtr(M+1))
    ALLOCATE(csrPVal(NNZP))
    
    csrPVal = (/(1.0D0,0.0D0),(1.0D0,0.0D0) ,(4.0D0,0.0D0) ,(0.5D0,0.0D0),(1.0D0,0.0D0) ,(-6.5D0,0.0D0) ,(1.0D0,0.0D0)/)
    csrPColInd = (/1 ,4 ,3 ,1 ,4 ,2 ,5 /)
    csrPRowPtr = (/1 ,3 ,4 ,5 ,6 ,8 /)  
    

    print*,'EXAMPLE PROGRAM FOR mkl_sparse_sypr'
    print*,'--------------------------------------------------------'


!   Create CSR matrix A
    i = MKL_SPARSE_Z_CREATE_CSR(csrA,SPARSE_INDEX_BASE_ONE,M,N,csrRowPtr,csrRowPtr(2),csrColInd,csrVal)

!   Create matrix descriptor
    !descrA % TYPE = SPARSE_MATRIX_TYPE_GENERAL
    descrA % TYPE = SPARSE_MATRIX_TYPE_SYMMETRIC
    descrA % MODE = SPARSE_FILL_MODE_UPPER
    descrA % DIAG = SPARSE_DIAG_NON_UNIT

!   Analyze sparse matrix; chose proper kernels and workload balancing strategy
    info = MKL_SPARSE_OPTIMIZE(csrA)
    
    
!   Create CSR matrix P
    i = MKL_SPARSE_Z_CREATE_CSR(csrP,SPARSE_INDEX_BASE_ONE,M,N,csrPRowPtr,csrPRowPtr(2),csrPColInd,csrPVal)

!   Create matrix descriptor
    descrP % TYPE = SPARSE_MATRIX_TYPE_GENERAL

!   Analyze sparse matrix; chose proper kernels and workload balancing strategy
    info = MKL_SPARSE_OPTIMIZE(csrP)
    
        
    ! Single Stage Computations 
    info = mkl_sparse_sypr (SPARSE_OPERATION_CONJUGATE_TRANSPOSE, csrP, csrA, descrA, csrD, SPARSE_STAGE_FULL_MULT)

! export the matrix D in CSR format matrix from the internal representation
    info = mkl_sparse_z_export_csr (csrD, indexing, nrowsD, ncolsD, rowsD_start, rowsD_end, colD_indx, Dvalues)
    
    info = mkl_sparse_order(csrD)
    
!   Converting C into Fortran pointers
    call C_F_POINTER(rowsD_start, rowsD_start_f, [nrowsD])
    call C_F_POINTER(rowsD_end  , rowsD_end_f  , [nrowsD]) 
    call C_F_POINTER(colD_indx  , colD_indx_f  , [rowsD_end_f(nrowsD)-indexing])
    call C_F_POINTER(Dvalues    , Dvalues_f    , [rowsD_end_f(nrowsD)-indexing])

  
!   Release internal representation of CSR matrix
    info = MKL_SPARSE_DESTROY(csrA)
    info = MKL_SPARSE_DESTROY(csrP)
    info = MKL_SPARSE_DESTROY(csrD)
    
END PROGRAM TestSPBLASProgram

 

In response to Gennady_F_Intel
0 Kudos
Copy link
Razmo86
Beginner
‎08-19-2021 11:57 AM
760 Views

@Gennady_F_Intel Thanks for looking into this issue. Here is the test program: 


    

!===============================================================================

!
! Consider the matrix A 
!
!                 |   1       -1+3i   0   -3+6i  0   |
!                 |  -1+3i     5      0    0     8   |
!   A    =        |   0        0      4    6     4   |,
!                 |  -3+6i     0      6    7     0   |
!                 |   0        8      4    0    -5   |
!
!  The matrix A is represented in a one-based compressed sparse row (CSR) storage
!  scheme with three arrays: Only the upper triangular part is stored
!
!         values  = ( 1 -1+3i -3+6i 5 8 4 6 4 7 -5 )
!         columns = ( 1 2 4 2 5 3 4 5 4 5 )
!         rowIndex = ( 1 4 6 9 10 11 )
!
!                 |   1        0      0       1      0   |
!                 |   0        0      4       0      0   |
!   P    =        |   0.5      0      0       0      0   |,
!                 |   0        0      0       1      0   |
!                 |   0     -6.5      0       0      1   |
!        
!         values  = ( 1 1 4 0.5 1 -6.5 1 )
!         columns = ( 1 4 3 1 4 2 5 )
!         rowIndex = ( 1 3 4 5 6 8 )   

!  The test performs the following operations :

!
    
!  The test performs the following operations :
!
!       The code computes D = P'AP using mkl_sparse_sypr. P is a MXM General sparse matrix
!       where A is a symmetric sparse matrix where only the upper triangular part is stored
!
    
!*******************************************************************************
PROGRAM TestSPBLASProgram

    USE MKL_SPBLAS
    USE ISO_C_BINDING
    IMPLICIT NONE

    INTEGER M, N, NNZ,NNZP, i, info,j
!   *****************************************************************************
!   Sparse representation of the matrix A and P
!   *****************************************************************************
    INTEGER, ALLOCATABLE :: csrColInd(:), csrRowPtr(:),csrPColInd(:), csrPRowPtr(:)
    COMPLEX*16, ALLOCATABLE :: csrVal(:),csrPVal(:)

!   Matrix descriptor
    TYPE(MATRIX_DESCR) descrA,descrP,descrD     ! Sparse matrix descriptor
!   CSR matrix representation 
    TYPE(SPARSE_MATRIX_T) csrA,csrP,csrD        ! Structure with sparse matrix
!   *****************************************************************************
!   Declaration of local variables:
!   *****************************************************************************
 
    INTEGER :: nCol,nrowsD, ncolsD
    
    INTEGER(C_INT) :: indexing
    TYPE(C_PTR)    :: rowsD_start, rowsD_end, colD_indx, Dvalues
    
    INTEGER   , POINTER :: rowsD_start_f(:), rowsD_end_f(:), colD_indx_f(:)
    COMPLEX*16, POINTER :: Dvalues_f(:)
    
    

    NNZ = 10
    ALLOCATE(csrColInd(NNZ))
    ALLOCATE(csrRowPtr(M+1))
    ALLOCATE(csrVal(NNZ))
    
    csrVal = (/(1.0D0,0.0D0), (-1.0D0,3.0D0) ,(-3.0D0,6.0D0), (5.0D0,0.0D0) ,(8.0D0,0.0D0) ,(4.0D0,0.0D0) ,(6.0D0,0.0D0), (4.0D0,0.0D0), (7.0D0,0.0D0), (-5.0D0,0.0D0)/)
    csrColInd = (/ 1, 2, 4, 2, 5, 3, 4, 5, 4, 5 /)
    csrRowPtr = (/1, 4, 6, 9, 10, 11/)
    
    
    
    M = 5
    N = 5
    NNZP = 6
    ALLOCATE(csrPColInd(NNZP))
    ALLOCATE(csrPRowPtr(M+1))
    ALLOCATE(csrPVal(NNZP))
    
    csrPVal = (/(1.0D0,0.0D0),(1.0D0,0.0D0) ,(4.0D0,0.0D0) ,(0.5D0,0.0D0),(1.0D0,0.0D0) ,(-6.5D0,0.0D0) ,(1.0D0,0.0D0)/)
    csrPColInd = (/1 ,4 ,3 ,1 ,4 ,2 ,5 /)
    csrPRowPtr = (/1 ,3 ,4 ,5 ,6 ,8 /)  
    

    print*,'EXAMPLE PROGRAM FOR mkl_sparse_sypr'
    print*,'--------------------------------------------------------'


!   Create CSR matrix A
    i = MKL_SPARSE_Z_CREATE_CSR(csrA,SPARSE_INDEX_BASE_ONE,M,N,csrRowPtr,csrRowPtr(2),csrColInd,csrVal)

!   Create matrix descriptor
    !descrA % TYPE = SPARSE_MATRIX_TYPE_GENERAL
    descrA % TYPE = SPARSE_MATRIX_TYPE_SYMMETRIC
    descrA % MODE = SPARSE_FILL_MODE_UPPER
    descrA % DIAG = SPARSE_DIAG_NON_UNIT

!   Analyze sparse matrix; chose proper kernels and workload balancing strategy
    info = MKL_SPARSE_OPTIMIZE(csrA)
    
    
!   Create CSR matrix P
    i = MKL_SPARSE_Z_CREATE_CSR(csrP,SPARSE_INDEX_BASE_ONE,M,N,csrPRowPtr,csrPRowPtr(2),csrPColInd,csrPVal)

!   Create matrix descriptor
    descrP % TYPE = SPARSE_MATRIX_TYPE_GENERAL

!   Analyze sparse matrix; chose proper kernels and workload balancing strategy
    info = MKL_SPARSE_OPTIMIZE(csrP)
    
        
    ! Single Stage Computations 
    info = mkl_sparse_sypr (SPARSE_OPERATION_CONJUGATE_TRANSPOSE, csrP, csrA, descrA, csrD, SPARSE_STAGE_FULL_MULT)

! export the matrix D in CSR format matrix from the internal representation
    info = mkl_sparse_z_export_csr (csrD, indexing, nrowsD, ncolsD, rowsD_start, rowsD_end, colD_indx, Dvalues)
    
    info = mkl_sparse_order(csrD)
    
!   Converting C into Fortran pointers
    call C_F_POINTER(rowsD_start, rowsD_start_f, [nrowsD])
    call C_F_POINTER(rowsD_end  , rowsD_end_f  , [nrowsD]) 
    call C_F_POINTER(colD_indx  , colD_indx_f  , [rowsD_end_f(nrowsD)-indexing])
    call C_F_POINTER(Dvalues    , Dvalues_f    , [rowsD_end_f(nrowsD)-indexing])

  
!   Release internal representation of CSR matrix
    info = MKL_SPARSE_DESTROY(csrA)
    info = MKL_SPARSE_DESTROY(csrP)
    info = MKL_SPARSE_DESTROY(csrD)
    
END PROGRAM TestSPBLASProgram
0 Kudos
Copy link
Kirill_V_Intel
Employee
‎08-19-2021 02:47 PM
743 Views

Hi!

I'm pretty sure the reason for what you see is a misleading wording in documentation. Routine mkl_sparse_sypr supports symmetric matrices A for real data types and hermitian (only) A for complex case [while the docs say "B and C are symmetric or Hermitian matrices" as if symmetric works for complex matrices].

E.g., a quick implicit proof: if you change 
descrA % TYPE = SPARSE_MATRIX_TYPE_SYMMETRIC
to
descrA % TYPE = SPARSE_MATRIX_TYPE_HERMITIAN

you'll get same result. I haven't checked but I believe that is the correct result if matrix A is treated as Hermitian [let me know if you think this is incorrect].

If you need this functionality, our TCE can help you submit a FR, so that we can extend mkl-sparse_sypr to work for your case (should be straightforward).

 

Best,
Kirill

Copy link
Razmo86
Beginner
‎08-20-2021 05:59 AM
722 Views
In response to Kirill_V_Intel

@Kirill_V_Intel Thanks for your answer. Correct, I have already verified that the routine is working correctly for real symmetric and Hermitian complex matrices. It would be great if you could extend mkl-sparse_sypr to symmetric complex matrices as well. Would you please let me know how I should process with the FR submission? 

 

Regards   

In response to Kirill_V_Intel
0 Kudos
Copy link
Gennady_F_Intel
Moderator
‎08-20-2021 07:27 AM
713 Views

Razmo, the official channel to submit the Feature Request to the Intel Online Service Center - https://supporttickets.intel.com/servicecenter?lang=en-US



0 Kudos
Copy link
Gennady_F_Intel
Moderator
‎09-30-2021 08:26 PM
549 Views

Intel oneAPI Math Kernel Library (oneMKL) version 2021.4 is now available. The MKL Developer Reference has been updated.




0 Kudos
Copy link
Gennady_F_Intel
Moderator
‎09-30-2021 08:26 PM
549 Views

This issue has been resolved and we will no longer respond to this thread. If you require additional assistance from Intel, please start a new thread. Any further interaction in this thread will be considered community only.


0 Kudos
Copy link
Reply

For more complete information about compiler optimizations, see our Optimization Notice.