Dear All,
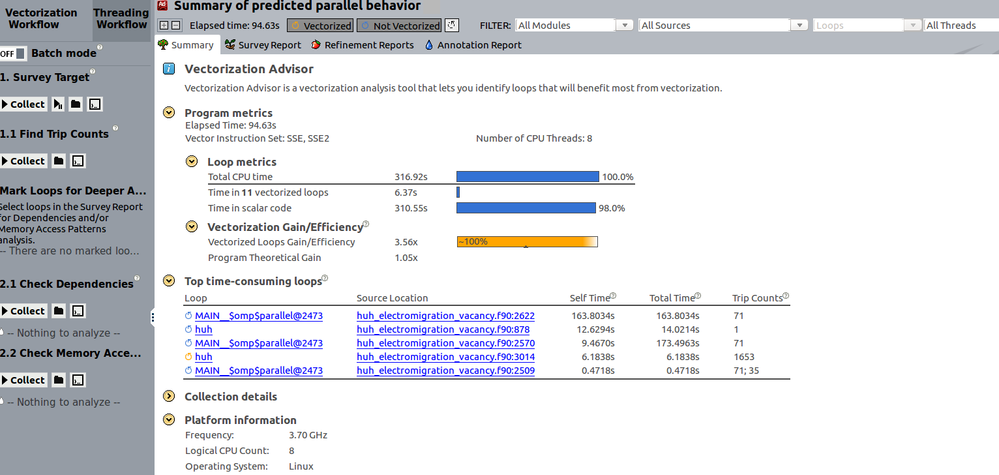
I analyzed my code using adviser recently and this is a snapshot of the code performance. I am including the portion of the code which causes tremendous slow down here. Can someone give me a couple of hints and examples to start correcting the code?!
Source code :
2473 !$OMP PARALLEL default(none) & 36.706s 11.29%
2474 !$OMP private(i,j,n,k,kk) & !! indice for Do loop
2475 !$OMP private(p11,p12,p13,p14,p21,p22,p23,p24) &
2476 !$OMP private(p31,p32,p33,p34,p41,p42,p43,p44) &
2477 !$OMP private(c11,c12,c13,c14,c21,c22,c23,c24) &
2478 !$OMP private(c31,c32,c33,c34,c41,c42,c43,c44) &
2479 !$OMP private(cs11,cs12,cs13,cs14,ci21,ci22,ci23,ci24) &
2480 !$OMP private(cl31,cl32,cl33,cl34,ce41,ce42,ce43,ce44) &
2481 !$OMP private(PHIC051,PHIC052,PHIC053,PHIC054) &
2482 !$OMP private(PSI11,PSI12,PSI13,PSI14) &
2483 !$OMP private(APK1,APK2,APK3,APK4) &
2484 !$OMP private(ph,pdx,pdy,pc,pd,ome_nkk,ome_kkk) &
2485 !$OMP private(pxxk,pxxkk,pxxp) &
2486 !$OMP private(del_psum1,result,result1,TIME) &
2487 !$OMP private(ick,msn,nop,pkk,psum1,psum22,ptot) &
2488 !$OMP private(pxxary,pxxn) &
2489 !$OMP shared(csn_s,dt,dx,epsgb,epsk,epsl,epss,gc3s,gc6s5,gcu_l) &
2490 !$OMP shared(gcu_s,gsn_l,gsn_s,l0l,l0s,l1l,l1s,l2l,ml,ms,omegb) &
2491 !$OMP shared(omek,omel,omes) &
2492 !$OMP shared(weight,eptime,eptime1,freq,zi,ei,kb) &
2493 !$OMP shared(ZEKT,EKT,EPQ) &
2494 !$OMP shared(am,ck,cn,dfk,eps,eps_kkk,eps_nkk,fk,fn) &
2495 !$OMP shared(ome,pa,pb) &
2496 !$OMP shared(CS05I,CS05J,CE05I,CE05J,CI05I,CI05J,CL05I,CL05J) & !! Input outside from parallel zone
2497 !$OMP shared(SUMIMC,NNN,NNN1,aa) & !! Input outside from parallel zone
2498 !$OMP shared(ce,ci,cl,cs,DDDI,DDDJ,PHI05I,PHI05J,SSSI,SSSJ) & !! Input outside from parallel zone
2499 !$OMP shared(APV1,APV2,APV3,APV4,APV11,APV21,APV31,APV41) &
2500 !$OMP shared(c1,phi1,c2,phi2,psi,Exc,Eyc,Ex,Ey)
2501 !$OMP Do
2502
2503 DO I=0, IG, 1 0.961s 0.19%
2504 DO J=0, JG, 1
2505
2506 !***** CALCULATE NEXT PHI VALUE *****
2507 NOP=0
2508
2509 DO N=1,NPP 0.072s 0.02% 0.472s 0.09%
2510 IF (PHI1(N,I,J).GT.0.0) THEN 0.032s 0.01%
2511 MSN(N)=1
2512 PXXARY(N)=(PHI1(N,I+1,J)+PHI1(N,I-1,J)+PHI1(N,I,J+1) & 0.040s 0.01% Divisions
2513 +PHI1(N,I,J-1)-4.0*PHI1(N,I,J))/(DX*DX) 0.042s 0.01%
2514
2515 ELSEIF (PHI1(N,I,J).EQ.0.0.AND.PHI1(N,I-1,J).GT.0.0) THEN 0.146s 0.04% 0.961s 0.19%
2516 MSN(N)=1
2517 PXXARY(N)=(PHI1(N,I+1,J)+PHI1(N,I-1,J)+PHI1(N,I,J+1) &
2518 +PHI1(N,I,J-1)-4.0*PHI1(N,I,J))/(DX*DX)
2519
2520 ELSEIF (PHI1(N,I,J).EQ.0.0.AND.PHI1(N,I,J-1).GT.0.0) THEN 0.070s 0.02%
2521 MSN(N)=1
2522 PXXARY(N)=(PHI1(N,I+1,J)+PHI1(N,I-1,J)+PHI1(N,I,J+1) &
2523 +PHI1(N,I,J-1)-4.0*PHI1(N,I,J))/(DX*DX) 0.008s 0.00%
2524
2525 ELSEIF (PHI1(N,I,J).EQ.0.0.AND.PHI1(N,I+1,J).GT.0.0) THEN 0.034s 0.01%
2526 MSN(N)=1
2527 PXXARY(N)=(PHI1(N,I+1,J)+PHI1(N,I-1,J)+PHI1(N,I,J+1) &
2528 +PHI1(N,I,J-1)-4.0*PHI1(N,I,J))/(DX*DX)
2529
2530 ELSEIF (PHI1(N,I,J).EQ.0.0.AND.PHI1(N,I,J+1).GT.0.0) THEN 0.070s 0.02%
2531 MSN(N)=1
2532 PXXARY(N)=(PHI1(N,I+1,J)+PHI1(N,I-1,J)+PHI1(N,I,J+1) &
2533 +PHI1(N,I,J-1)-4.0*PHI1(N,I,J))/(DX*DX)
2534 ELSE
2535 MSN(N)=0
2536 PXXARY(N)=0.0 0.030s 0.01%
2537 ENDIF
2538
2539 PHI2(N,I,J)=PHI1(N,I,J) ! only phi in interface region will be updated. 0.118s 0.04%
2540 NOP=NOP+MSN(N) ! number of coexisting phases at a grid (i,j). 0.108s 0.03% Type Conversions
2541 END DO
2542
2543 !********************************************************************************
2545
2546 108 IF(NOP.GE.2) THEN
2547 ICK=0
2548
2549 DO N=1, NPP
2550 IF(MSN(N).EQ.1) THEN 0.062s 0.02% 0.110s 0.02%
2551 PXXN=PXXARY(N) !(PHI1(N,I+1,J)+PHI1(N,I-1,J)+PHI1(N,I,J+1)+PHI1(N,I,J-1)-4.0*PHI1(N,I,J))/(DX*DX) 0.060s 0.02%
2552
2553 IF(N.EQ.1) THEN
2554 CN = CS(I,J)
2555 FN = FS(CN) 0.024s 0.01%
2556 ELSEIF(N.EQ.NPP) THEN
2557 CN = CL(I,J)
2558 FN = FL(CN)
2559 ELSEIF(N.GE.NPPK.AND.N.LT.NPP) THEN
2560 CN = CI(I,J) 0.032s 0.01%
2561 FN = FI(CN) 0.064s 0.02%
2562 ELSE
2563 CN = CE(I,J) 0.012s 0.00%
2564 FN = FE(CN) 0.054s 0.02%
2565 ENDIF
2566
2567 PTOT = 0.0 18.852s 5.80%
2568
2569 DO K=1, NPP
2570 IF(K.NE.N.AND.MSN(K).EQ.1) THEN 1.304s 0.40% 173.496s 34.85%
2571 PXXK=PXXARY(K) !(PHI1(K,I+1,J)+PHI1(K,I-1,J)+PHI1(K,I,J+1)+PHI1(K,I,J-1)-4.0*PHI1(K,I,J))/(DX*DX) 0.148s 0.05%
2572 PXXP=PXXK-PXXN 0.092s 0.03%
2573
2574 IF(K.EQ.1) THEN 0.430s 0.13%
2575 CK = CS(I,J)
2576 FK = FS(CK) 0.080s 0.02% Divisions
2577 DFK = DFS(CK) 0.034s 0.01% Divisions
2578 ELSEIF(K.EQ.NPP) THEN
2579 CK = CL(I,J) 0.038s 0.01%
2580 FK = FL(CK) 0.209s 0.06% Divisions
2581 DFK = DFL(CK) 0.130s 0.04% Divisions
2582 ELSEIF(K.GE.NPPK.AND.K.LT.NPP) THEN
2583 CK = CI(I,J) 0.164s 0.05%
2584 FK = FI(CK) 0.826s 0.25% Divisions
2585 DFK = DFI(CK) 0.431s 0.13% Divisions
2586 ELSE
2587 CK = CE(I,J) 0.195s 0.06%
2588 FK = FE(CK) 0.554s 0.17% Divisions
2589 DFK = DFE(CK) 0.372s 0.11% Divisions
2590 ENDIF
2591
2592 IF((N.EQ.NPP).OR.(K.EQ.NPP)) THEN 0.080s 0.02%
2593 EPS(I,J)=EPSL 0.022s 0.01%
2594 OME(I,J)=OMEL 0.008s 0.00%
2595 AM(I,J)=ML
2596 ELSEIF((N.EQ.1).OR.(K.EQ.1)) THEN
2597 EPS(I,J)=EPSS 0.008s 0.00%
2598 OME(I,J)=OMES 0.010s 0.00%
2599 AM(I,J)=MS 0.008s 0.00%
2600 elseif(((n.ge.2.and.n.lt.nppk).and.(k.ge.nppk.and.k.lt.npp-1)).or. & 0.350s 0.11%
2601 ((k.ge.2.and.k.lt.nppk).and.(n.ge.nppk.and.n.lt.npp-1))) then 0.030s 0.01%
2602 EPS(I,J)=EPSK 0.172s 0.05%
2603 OME(I,J)=OMEK 0.242s 0.07%
2604 AM(I,J)=MS 0.186s 0.06%
2605 elseif(((n.ge.2.and.n.lt.nppk).and.(k.ge.nppk.and.k.lt.npp-1)).or. & 0.060s 0.02%
2606 ((k.ge.2.and.k.lt.nppk).and.(n.ge.nppk.and.n.lt.npp-1))) then 0.010s 0.00%
2607 EPS(I,J)=EPSK
2608 OME(I,J)=OMEK
2609 AM(I,J)=MS
2610 elseif((n.ge.2.and.n.lt.nppk).or.(k.ge.2.and.k.lt.nppk)) then 0.012s 0.00%
2611 EPS(I,J)=EPSK
2612 OME(I,J)=OMEK
2613 AM(I,J)=MS
2614 ELSE
2615 EPS(I,J)=EPSGB 0.199s 0.06%
2616 OME(I,J)=OMEGB 0.028s 0.01%
2617 AM(I,J)=MS 0.030s 0.01%
2618 ENDIF
2619
2620 PKK=0.0 0.028s 0.01%
2621 DO KK=1, NPP 0.016s 0.00%
2622 IF(KK.NE.N.AND.KK.NE.K.AND.MSN(KK).EQ.1.AND.KK.NE.NPP) THEN 14.918s 4.59% 163.803s 32.90%
2623 PXXKK=(PHI1(KK,I+1,J)+PHI1(KK,I-1,J)+PHI1(KK,I,J+1) & 19.070s 5.87% Divisions
2624 +PHI1(KK,I,J-1)-4.*PHI1(KK,I,J))/(DX*DX) ! Laplacian phi 11.133s 3.42%
2625 IF(N.EQ.NPP) THEN 0.737s 0.23%
2626 OME_NKK=OMEL 0.266s 0.08%
2627 EPS_NKK=EPSL 0.472s 0.15%
2628 ELSEIF(N.EQ.1) THEN
2629 OME_NKK=OMES 0.430s 0.13%
2630 EPS_NKK=EPSS 0.250s 0.08%
2631 ELSEIF(N.EQ.NPP-1) THEN
2632 OME_NKK=OMEGB 34.930s 10.74%
2633 EPS_NKK=EPSGB 4.891s 1.50%
2634 ELSEIF(N.GE.NPPK.AND.N.LT.NPP-1) THEN
2635 OME_NKK=OMEGB
2636 EPS_NKK=EPSGB
2637 ELSE
2638 OME_NKK=OMEGB
2639 EPS_NKK=EPSGB
2640 ENDIF
2641
2642 IF(K.EQ.NPP) THEN 0.865s 0.27%
2643 OME_KKK=OMEL 0.036s 0.01%
2644 EPS_KKK=EPSL 0.908s 0.28%
2645 ELSEIF(K.EQ.1) THEN
2646 OME_KKK=OMES 0.008s 0.00%
2647 EPS_KKK=EPSS 0.448s 0.14%
2648 ELSEIF(K.EQ.NPP-1) THEN
2649 OME_KKK=OMEGB 1.208s 0.37%
2650 EPS_KKK=EPSGB 39.524s 12.16%
2651 ELSEIF(K.GE.NPPK.AND.K.LT.NPP-1) THEN
2652 OME_KKK=OMEGB
2653 EPS_KKK=EPSGB
2654 ELSE
2655 OME_KKK=OMEGB
2656 EPS_KKK=EPSGB
2657 ENDIF
2658
2659 PKK=PKK+0.5*(EPS_NKK**2.-EPS_KKK**2.)*PXXKK & 7.826s 2.41%
2660 +(OME_NKK-OME_KKK)*PHI1(KK,I,J) 4.963s 1.53%
2661 ENDIF
2662 ENDDO 21.098s 6.49%
2663
2664 PA(I,J)=0.5*(EPS(I,J)**2.0)*PXXP ! Epsilon term 0.240s 0.07%
2665 PB(I,J)=OME(I,J)*(PHI1(K,I,J)-PHI1(N,I,J)) ! Omega term 0.482s 0.15%
2666
2667 PH=1.0
2668 PC=PH*(FN-FK-(CN-CK)*DFK) ! Free energy term 0.414s 0.13%
2669
2670 PDX=(8.0*(PSI(I+1,J)-PSI(I-1,J))-(PSI(I+2,J)-PSI(I-2,J)))/(12.*DX)
2671 PDY=(8.0*(PSI(I,J+1)-PSI(I,J-1))-(PSI(I,J+2)-PSI(I,J-2)))/(12.*DX)
2672
2673 !PD=sigmac(i,j)*sqrt(PDX**2.+PDY**2.)/freq
2674 PD=sqrt((SSSI(I,J)*PDX)**2.+(SSSJ(I,J)*PDY)**2.)/freq*EPTIME*0.0
2675
2676 ! PTOT=PTOT-AM*DT*(PA+PB+PC+PD+PKK) ! Summation value
2677
2678 PTOT(I,J)=PTOT(I,J)-AM(I,J)*DT*(PA(I,J)+PB(I,J)+PC+PD+PKK) ! summation value 1.736s 0.53%
2679
2680 ENDIF
2681 ENDDO 0.706s 0.22%
2682
2683 PHI2(N,I,J)=PHI1(N,I,J)+(2.0/NOP)*PTOT(I,J) ! phi value at the next time step 0.092s 0.03% Divisions; Type Conversions
2684
2685 IF(PHI2(N,I,J).GT.1.0) THEN 0.019s 0.01%
2686 PHI2(N,I,J)=1.0
2687 ICK=1
2688 EXIT
2689 ELSEIF(PHI2(N,I,J).LT.0.0) THEN
2690 PHI2(N,I,J)=0.0
2691 ICK=2
2692 EXIT
2693 ENDIF
2694
2695 !********** CHECKING FOR NaN ***********
2696
2697 !IF (ieee_is_nan(C1(I,J)) THEN
2698 result1=(PHI2(N,I,J))
2699 IF (ISNAN(result1))THEN 0.050s 0.02%
2700 WRITE(*,*)'********** NaN value in PHI PDE!! ************'
2701 WRITE(*,*) '# of coexisting phases at this point is:',NOP
2702 WRITE(*,*) 'I,J,N,NNN,PHI2(N,I,J)'
2703 WRITE(*,*) I,J,N,NNN,result1
2704 WRITE(*,*)
2705 WRITE(*,*) 'CS(I,J),CI(I,J),CE(I,J),CL(I,J)'
2706 WRITE(*,*) CS(I,J),CI(I,J),CE(I,J),CL(I,J)
2707 WRITE(*,*)
2708 WRITE(*,*) 'PB contents: PHI1(K,I,J),PHI1(N,I,J)'
2709 WRITE(*,"(4F12.2)") PHI1(K,I,J),PHI1(N,I,J)
2710 WRITE(*,*)
2711 WRITE(*,*) 'CL(I,J),FL(CK),DFL(CK)'
2712 WRITE(*,*) CL(I,J),FL(CK),DFL(CK)
2713 WRITE(*,*)
2714 WRITE(*,*) 'CS(I,J),FS(CK),DFS(CK)'
2715 WRITE(*,*) CS(I,J),FS(CK),DFS(CK)
2716 WRITE(*,*)
2717 WRITE(*,*) 'CI(I,J),FI(CK),DFI(CK)'
2718 WRITE(*,*) CI(I,J),FI(CK),DFI(CK)
2719 WRITE(*,*) '********** NaN value in Field equation! ************'
2720 pause
2721
2722 ENDIF
2723
2724 ENDIF
2725
2726 ENDDO 0.048s 0.01%
2727
2729 IF(ICK.EQ.1) THEN
2730 DO K=1,NPP 0.020s 0.01% 0.008s 0.00%
2731 IF(K.NE.N) PHI2(K,I,J)=0.0
2732 END DO
2733 ELSEIF(ICK.EQ.2) THEN ! recalculate phi2 after phi2(N,I,J)=0 and msn(N)=0 (hopefully assuming phi1(N,I,J)=0)
2734 MSN(N)=0
2735 IF(NOP.EQ.2) THEN 0.008s 0.00%
2736 DO K=1,NPP 0.012s 0.00%
2737 IF(MSN(K).EQ.1) PHI2(K,I,J)=1.0 0.012s 0.00%
2738 END DO
2739 ELSEIF(NOP.GT.2) THEN
2740 NOP=NOP-1
2741 GOTO 108
2742 ENDIF
2743 ENDIF
2744
2745 !*****
2749 PSUM1=0.0 0.012s 0.00% Unpacks
2750 DO N=1,NPP 0.012s 0.00%
2751 PSUM1=PSUM1+PHI2(N,I,J) 0.012s 0.00%
2752 END DO
2753 IF(PSUM1.NE.1.0) THEN
2754 DEL_PSUM1=1.0-PSUM1
2755
2756 psum22=0.0
2757 do n=1,npp 0.034s 0.01%
2758 if(msn(n).eq.1) then 0.018s 0.01%
2759 psum22=psum22+0.5-dabs(phi2(n,i,j)-0.5) 0.016s 0.00%
2760 endif
2761 enddo
2762 DO N=1, NPP
2763 IF(MSN(N).EQ.1) THEN 0.012s 0.00% 0.048s 0.01%
2764 PHI2(N,I,J)=PHI2(N,I,J)+DEL_PSUM1 & 0.024s 0.01%
2765 *(0.5-dabs(phi2(n,i,j)-0.5))/(psum22) !!/DFLOAT(NOP) !!*PHI2(N,I,J)/PSUM1 !!! 0.012s 0.00% Divisions
2766 ENDIF
2767 END DO
2768 ENDIF
2769
2770 ENDIF
2771
2773 ! PHI_i
2774 P11 = PHI05I(1,I,J) !H(PHI05I(1,I,J)) ! (I+1/2,J) 0.042s 0.01%
2775 P12 = PHI05I(1,I-1,J) !H(PHI05I(1,I-1,J)) ! (I-1/2,J) 0.030s 0.01%
2776 P13 = PHI05J(1,I,J) !H(PHI05J(1,I,J)) ! (I,J+1/2)
2777 P14 = PHI05J(1,I,J-1) !H(PHI05J(1,I,J-1)) ! (I,J-1/2)
2778
2779 P41 = PHI05I(4,I,J) !H(PHI05I(4,I,J)) ! (I+1/2,J)
2780 P42 = PHI05I(4,I-1,J) !H(PHI05I(4,I-1,J)) ! (I-1/2,J)
2781 P43 = PHI05J(4,I,J) !H(PHI05J(4,I,J)) ! (I,J+1/2) 0.008s 0.00%
2782 P44 = PHI05J(4,I,J-1) !H(PHI05J(4,I,J-1)) ! (I,J-1/2)
2783
2784 P21 = PHI05I(2,I,J) !H(PHI05I(2,I,J)) ! (I+1/2,J) 0.008s 0.00%
2785 P22 = PHI05I(2,I-1,J) !H(PHI05I(2,I-1,J)) ! (I-1/2,J) 0.008s 0.00%
2786 P23 = PHI05J(2,I,J) !H(PHI05J(2,I,J)) ! (I,J+1/2)
2787 P24 = PHI05J(2,I,J-1) !H(PHI05J(2,I,J-1)) ! (I,J-1/2)
2788
2789 P31 = PHI05I(3,I,J) !H(PHI05I(3,I,J)) ! (I+1/2,J) 0.012s 0.00%
2790 P32 = PHI05I(3,I-1,J) !H(PHI05I(3,I-1,J)) ! (I-1/2,J)
2791 P33 = PHI05J(3,I,J) !H(PHI05J(3,I,J)) ! (I,J+1/2)
2792 P34 = PHI05J(3,I,J-1) !H(PHI05J(3,I,J-1)) ! (I,J-1/2) 0.008s 0.00%
2793
2794 !! dC_i
2795 C11 = CS(I+1,J)-CS(I,J);
2796 C12 = CS(I,J)-CS(I-1,J);
2797 C13 = CS(I,J+1)-CS(I,J);
2798 C14 = CS(I,J)-CS(I,J-1);
2799
2800 C41 = CE(I+1,J)-CE(I,J);
2801 C42 = CE(I,J)-CE(I-1,J);
2802 C43 = CE(I,J+1)-CE(I,J);
2803 C44 = CE(I,J)-CE(I,J-1);
2804
2805 C21 = CI(I+1,J)-CI(I,J);
2806 C22 = CI(I,J)-CI(I-1,J) 0.012s 0.00%
2807 C23 = CI(I,J+1)-CI(I,J);
2808 C24 = CI(I,J)-CI(I,J-1)
2809
2810 C31 = CL(I+1,J)-CL(I,J);
2811 C32 = CL(I,J)-CL(I-1,J)
2812 C33 = CL(I,J+1)-CL(I,J);
2813 C34 = CL(I,J)-CL(I,J-1)
2814
2815 CS11 = CS05I(I,J); CS12 = CS05I(I-1,J)
2816 CS13 = CS05J(I,J); CS14 = CS05J(I,J-1)
2817
2818 CE41 = CE05I(I,J); CE42 = CE05I(I-1,J)
2819 CE43 = CE05J(I,J); CE44 = CE05J(I,J-1)
2820
2821 CI21 = CI05I(I,J); CI22 = CI05I(I-1,J)
2822 CI23 = CI05J(I,J); CI24 = CI05J(I,J-1)
2823
2824 CL31 = CL05I(I,J); CL32 = CL05I(I-1,J)
2825 CL33 = CL05J(I,J); CL34 = CL05J(I,J-1)
2826
2827 ! PHI_i*C_i
2828 PHIC051=P11*CS11+P21*CI21+P31*CL31+P41*CE41
2829 PHIC052=P12*CS12+P22*CI22+P32*CL32+P42*CE42
2830 PHIC053=P13*CS13+P23*CI23+P33*CL33+P43*CE43 0.008s 0.00%
2831 PHIC054=P14*CS14+P24*CI24+P34*CL34+P44*CE44 0.028s 0.01%
2832
2833 ! dPSI
2834 PSI11 = PSI(I+1,J)-PSI(I,J); PSI12 = PSI(I,J)-PSI(I-1,J)
2835 PSI13 = PSI(I,J+1)-PSI(I,J); PSI14 = PSI(I,J)-PSI(I,J-1)
2836
2837 APK1 = DDDI(I,J) *(P11*C11+P21*C21+P31*C31+P41*C41 &
2838 -ZEKT(I,J)*PHIC051*PSI11) 0.010s 0.00%
2840
2841 APK2 = DDDI(I-1,J)*(P12*C12+P22*C22+P32*C32+P42*C42 & 0.024s 0.01%
2842 -ZEKT(I,J)*PHIC052*PSI12)
2844
2845 APK3 = DDDJ(I,J) *(P13*C13+P23*C23+P33*C33+P43*C43 &
2846 -zekt(I,J)*PHIC053*PSI13)
2848
2849 APK4 = DDDJ(I,J-1)*(P14*C14+P24*C24+P34*C34+P44*C44 & 0.020s 0.01%
2850 -ZEKT(I,J)*PHIC054*PSI14)
2852
2853 C2(I,J) = C1(I,J)+DT*(APK1-APK2+APK3-APK4)/(DX*DX) 0.044s 0.01% Divisions
2854
2855 !! ****** CHECKING FOR STRANGE OR NaN values *****
2856 IF(C2(I,J).GE.1.0) THEN
2857 WRITE(*,*) 'TIME:',TIME
2858 WRITE(*,*) 'NNN,I,J, C1(I,J),C2(I,J)'
2859 WRITE(*,*) NNN,I,J, C1(I,J),C2(I,J), 'C2 VALUE IS STRANGE'
2860 C2(I,J)=(C2(I+1,J)+C2(I-1,J)+C2(I,J-1)+C2(I,J+1))/4
2861
2862 IF(PHI1(NPP,I,J).GE.0.85) C2(I,J) = 0.97
2863
2864 !C2(I,J) = C1(I,J)
2865 !STOP
2866
2867 ELSEIF(C2(I,J).LE.0.0) THEN
2868 WRITE(*,*) 'TIME:',TIME
2869 WRITE(*,*) 'NNN,I,J, C1(I,J),C2(I,J)'
2870 WRITE(*,*) NNN,I,J, C1(I,J),C2(I,J), 'C2 VALUE IS STRANGE'
2871 C2(I,J)=(C2(I+1,J)+C2(I-1,J)+C2(I,J-1)+C2(I,J+1))/4
2872
2873 IF(PHI1(NPP,I,J).GE.0.85) C2(I,J) = 0.97
2874
2875 !C2(I,J) = C1(I,J)
2876 !STOP
2877
2878 ENDIF
2879
2880 !********** CHECKING FOR NaN @ C Equation ***********
2881 !IF (ieee_is_nan(C1(I,J)) THEN
2882 result=(C2(I,J))
2883 IF (ISNAN(result))THEN
2884 WRITE(*,*) '!********** Found NaN @ C Equation *****************'
2885 WRITE(*,*) 'TIME:',TIME
2886 WRITE(*,*) 'I,J,NNN,result'
2887 WRITE(*,*) I,J,NNN,result
2888 WRITE(*,*) 'DT,DX,APK1,APK2,APK3,APK4'
2889 WRITE(*,*) DT,DX,APK1,APK2,APK3,APK4
2890 WRITE(*,*)
2891 WRITE(*,*) 'DDDI(I,J),P11,C11,P21,C21,P31,C31,P41,C41'
2892 WRITE(*,*) DDDI(I,J),P11,C11,P21,C21,P31,C31,P41,C41
2893 WRITE(*,*)
2894 WRITE(*,*) 'P13,C13,P23,C23,P33,C33,P43,C43'
2895 WRITE(*,*) P13,C13,P23,C23,P33,C33,P43,C43
2896 WRITE(*,*)
2897 WRITE(*,*) 'P12,C12,P22,C22,P32,C32,P42,C42'
2898 WRITE(*,*) P12,C12,P22,C22,P32,C32,P42,C42
2899 WRITE(*,*)
2900 WRITE(*,*) 'P14,C14,P24,C24,P34,C34,P44,C44'
2901 WRITE(*,*) P14,C14,P24,C24,P34,C34,P44,C44
2902 WRITE(*,*)
2903 WRITE(*,*) 'PHIC051,PHIC052,PHIC053,PHIC054'
2904 WRITE(*,*) PHIC051,PHIC052,PHIC053,PHIC054
2905 WRITE(*,*)
2906 WRITE(*,*) 'PSI11,PSI12,PSI13,PSI14'
2907 WRITE(*,*) PSI11,PSI12,PSI13,PSI14
2908 WRITE(*,*)
2909 WRITE(*,*) 'PSI(I+1,J),PSI(I,J),PSI(I,J),PSI(I-1,J)'
2910 WRITE(*,*) PSI(I+1,J),PSI(I,J),PSI(I,J),PSI(I-1,J)
2911 WRITE(*,*)
2912 WRITE(*,*) 'DDDI(I,J) *(P11*C11+P21*C21+P31*C31+P41*C41'
2913 WRITE(*,*) DDDI(I,J) *(P11*C11+P21*C21+P31*C31+P41*C41)
2914 WRITE(*,*) '!**************************************************'
2915
2916 STOP
2917 ENDIF
2918
2919 ENDDO
2920 ENDDO
Link Copied
Dear Tim,
Thanks a lot for the point that you made. I am not sure what you mean by the "information on effectiveness of parallelization". Here, I will try to elabrate more on what I have done so far. I compiled the code using:
ifort -g -O3 -qopt-report=5 -xHOST -simd huh_electromigration.f90 (serial mode)
ifort -g -O3 -qopt-report=5 -xHOST -simd -qopenmp huh_electromigration.f90 (OpenMP mode)
The Openmp runtime is the same as the serial run-time. I observe an exponential increase in the loop run-time. To be more precise, The 1st iteration run-time is 0.45 seconds and gradually it increases up to 1.8 seconds after 50 iterations and it goes on.
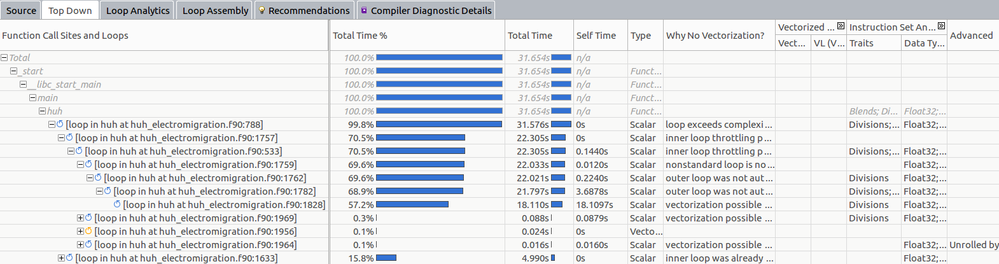
In addition, the Top Down section is as below:
From the above table, I noticed that the loop in row 1828 (row 73 in the below code) seems to be the main source of issue. This is because, that loop is the very inner loop and it costs 18.110 seconds to run. When I checked the loop content, there is this N variable inside the loop which comes from the top level Do loop. Is this the reason of slow down in the code?!
How should I rewrite the code to overcome the dependency of the loops with each other?
In addition, Intel Advisor is not providing any suggestion for this part.
Here is that portion of the code again:
DO I=0, IG, 1
DO J=0, JG, 1
108 IF(NOP(I,J).GE.2) THEN
ICK=0
DO N=1, NPP
IF(MSN(N,I,J).EQ.1) THEN
PXXN=PXXARY(N,I,J) !(PHI1(N,I+1,J)+PHI1(N,I-1,J)+PHI1(N,I,J+1)+PHI1(N,I,J-1)-4.0*PHI1(N,I,J))/(DX*DX)
IF(N.EQ.1) THEN
CN = CS(I,J)
FN = FS(CN)
ELSEIF(N.EQ.NPP) THEN
CN = CL(I,J)
FN = FL(CN)
ELSEIF(N.GE.NPPK.AND.N.LT.NPP) THEN
CN = CI(I,J)
FN = FI(CN)
ELSE
CN = CE(I,J)
FN = FE(CN)
ENDIF
PTOT = 0.0
DO K=1, NPP
IF(K.NE.N.AND.MSN(K,I,J).EQ.1) THEN
PXXK=PXXARY(K,I,J) !(PHI1(K,I+1,J)+PHI1(K,I-1,J)+PHI1(K,I,J+1)+PHI1(K,I,J-1)-4.0*PHI1(K,I,J))/(DX*DX) ! Laplacian phi
PXXP=PXXK-PXXN
IF(K.EQ.1) THEN
CK = CS(I,J)
FK = FS(CK)
DFK = DFS(CK)
ELSEIF(K.EQ.NPP) THEN
CK = CL(I,J)
FK = FL(CK)
DFK = DFL(CK)
ELSEIF(K.GE.NPPK.AND.K.LT.NPP) THEN
CK = CI(I,J)
FK = FI(CK)
DFK = DFI(CK)
ELSE
CK = CE(I,J)
FK = FE(CK)
DFK = DFE(CK)
ENDIF
IF((N.EQ.NPP).OR.(K.EQ.NPP)) THEN
EPS(I,J)=EPSL
OME(I,J)=OMEL
AM(I,J)=ML
ELSEIF((N.EQ.1).OR.(K.EQ.1)) THEN
EPS(I,J)=EPSS
OME(I,J)=OMES
AM(I,J)=MS
elseif(((n.ge.2.and.n.lt.nppk).and.(k.ge.nppk.and.k.lt.npp-1)).or. ((k.ge.2.and.k.lt.nppk).and.(n.ge.nppk.and.n.lt.npp-1))) then
EPS(I,J)=EPSK
OME(I,J)=OMEK
AM(I,J)=MS
elseif((n.ge.2.and.n.lt.nppk).or.(k.ge.2.and.k.lt.nppk)) then
EPS(I,J)=EPSK
OME(I,J)=OMEK
AM(I,J)=MS
ELSE
EPS(I,J)=EPSGB
OME(I,J)=OMEGB
AM(I,J)=MS
ENDIF
PKK=0.0
DO KK=1, NPP
IF(KK.NE.N.AND.KK.NE.K.AND.MSN(KK,I,J).EQ.1.AND.KK.NE.NPP) THEN
PXXKK=(PHI1(KK,I+1,J)+PHI1(KK,I-1,J)+PHI1(KK,I,J+1)+PHI1(KK,I,J-1)-4.*PHI1(KK,I,J))/(DX*DX) ! Laplacian phi
IF(N.EQ.NPP) THEN
OME_NKK=OMEL
EPS_NKK=EPSL
ELSEIF(N.EQ.1) THEN
OME_NKK=OMES
EPS_NKK=EPSS
ELSEIF(N.EQ.NPP-1) THEN
OME_NKK=OMEGB
EPS_NKK=EPSGB
ELSEIF(N.GE.NPPK.AND.N.LT.NPP-1) THEN
OME_NKK=OMEGB
EPS_NKK=EPSGB
ELSE
OME_NKK=OMEGB
EPS_NKK=EPSGB
ENDIF
IF(K.EQ.NPP) THEN
OME_KKK=OMEL
EPS_KKK=EPSL
ELSEIF(K.EQ.1) THEN
OME_KKK=OMES
EPS_KKK=EPSS
ELSEIF(K.EQ.NPP-1) THEN
OME_KKK=OMEGB
EPS_KKK=EPSGB
ELSEIF(K.GE.NPPK.AND.K.LT.NPP-1) THEN
OME_KKK=OMEGB
EPS_KKK=EPSGB
ELSE
OME_KKK=OMEGB
EPS_KKK=EPSGB
ENDIF
PKK=PKK+0.5*(EPS_NKK**2.-EPS_KKK**2.)*PXXKK + (OME_NKK-OME_KKK)*PHI1(KK,I,J)
ENDIF
ENDDO
PA(I,J)=0.5*(EPS(I,J)**2.0)*PXXP ! Epsilon term
PB(I,J)=OME(I,J)*(PHI1(K,I,J)-PHI1(N,I,J)) ! Omega term
PH=1.0
PC=PH*(FN-FK-(CN-CK)*DFK) ! Free energy term
PDX=(8.0*(PSI(I+1,J)-PSI(I-1,J))-(PSI(I+2,J)-PSI(I-2,J)))/(12.*DX)
PDY=(8.0*(PSI(I,J+1)-PSI(I,J-1))-(PSI(I,J+2)-PSI(I,J-2)))/(12.*DX)
!PD=sigmac(i,j)*sqrt(PDX**2.+PDY**2.)/freq
PD=sqrt((SSSI(I,J)*PDX)**2.+(SSSJ(I,J)*PDY)**2.)/freq!*EPTIME*0.0
! PTOT=PTOT-AM*DT*(PA+PB+PC+PD+PKK) ! Summation value
PTOT(I,J)=PTOT(I,J)-AM(I,J)*DT*(PA(I,J)+PB(I,J)+PC+PD+PKK) ! summation value
ENDIF
ENDDO
ENDDO
ENDDO
Tim P. wrote:
You haven't shown information on effectiveness of parallelization. You would need to separate the cases for specific values of the do loop variables and simplify the inner loops.
