Published July 14th, 2021
Santiago Miret is a deep learning researcher at Intel Labs, where he focuses on developing artificial intelligence (AI) solutions and exploring the intersection of AI and the physical sciences
Highlights:
- Neuroevolution-Enhanced Multi-Objective Optimization (NEMO) for Mixed-Precision Quantization delivers state-of-the-art compute speedups and memory improvements for artificial intelligence (AI) applications.
- Our research paper shows promising results for mixed-precision quantization, a neural network compression challenge, as well as general multi-objective problems using NEMO for large combinatorial search spaces.
Multi-Objective Optimization
Many situations that we encounter in our daily lives can surprisingly be expressed as multi-objective optimization problems. When we buy a new phone or laptop, we judge cost, performance, battery life, and many other factors at the same time. And almost always, it’s nearly impossible to find a product that has the best performance and battery life at the lowest cost. A laptop with the best performance and highest battery life often has the highest cost, while the cheapest one usually lags in the other factors. As such, we often end up deciding based on a set of options that we consider to be the best collection of solutions.
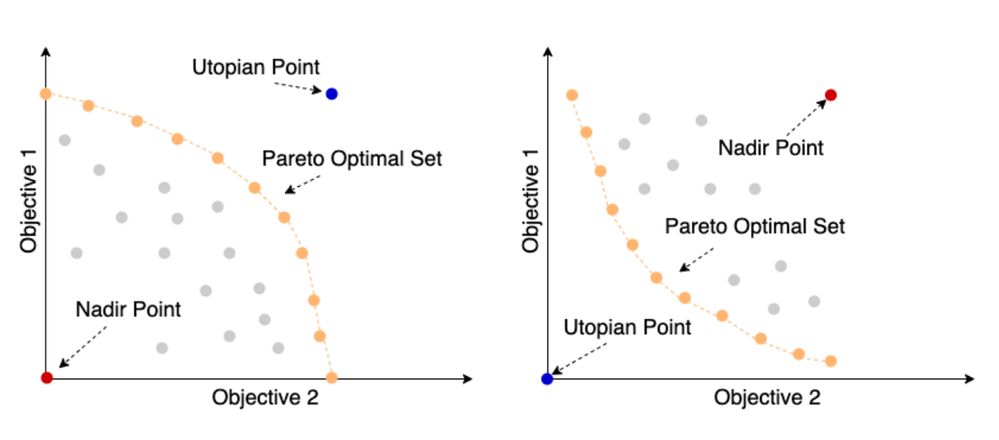
Many challenges in engineering, science, and design—and in daily life—involve these types of multi-objective optimization problems. These problems can be very complex and have a big influence on how we make decisions. When we have different choices that provide the highest performance or functionality along some dimension but not every single one (i.e., best in performance but worst in cost), they can be mathematically expressed as a Pareto optimal set, also known as a Pareto frontier. Specifically, the Pareto optimal set consists of solutions where no other solution can be better in at least one objective in the optimization space.
Figure 1. Example of Pareto frontiers with maximization of two objectives: for example, performance and battery life (right) and minimization of two objectives, such as cost and weight (left). The blue point is the Utopian Point, which is ideal along with all goals (highest performance, highest battery life, lowest cost). The red point is the Nadir Point, which is the worst point, along with all objectives (lowest performance, lowest battery life, highest cost). The Pareto frontiers are shown in orange and suboptimal solutions are shown in grey.
Optimizing AI Inference
One crucial challenge at Intel Labs is maximizing the performance of an AI model inference by applying different compression methods. This task naturally lends itself to a multi-objective formulation of three different dimensions:
- Task performance: how well a model performs on image classification.
- Memory footprint: how much memory the model consumes when deployed in inference.
- Speed of compute: how fast inference calculation can be performed on the underlying hardware.
In our recent paper, “Neuroevolution-Enhanced Multi-Objective Optimization for Mixed-Precision Quantization,” we developed a novel gradient-free method to determine mixed-precision quantization configurations of various AI workloads. Our method creates a Pareto optimal set of solutions for compressed models that deliver state-of-the-art compute speedups and memory improvements for various levels of trade-offs with task performance.
Based on the current research literature, our paper is the first study to treat mixed-precision quantization as a multi-objective optimization problem and effectively provide Pareto optimal sets of solutions for large ImageNet architectures, including ResNeXt-101-32x8d, one of the largest ImageNet workloads. Moreover, using our method, we have achieved competitive results to the state-of-the-art in-memory compression and superior compute acceleration for various points in our Pareto optimal set for Mobilenet-V2 and ResNet50.
Mixed-Precision Quantization
Mixed-precision quantization of neural networks is a technique that allows us to specify a heterogeneous set of computation precisions for different operations in the overall model architecture. This type of quantization enables us to put higher precisions on more important layers and lower precisions on less important layers to improve the computation efficiency. Reducing computation precision is a powerful compression tool because whenever computation is performed on any hardware system, the precision of the computation needs to be specified.
Having this ability is particularly important for large AI workloads with vast quantities of numerical operations on a collection of tensors. The effects of different levels of precision can be illustrated by performing computations with π, an irrational number with an infinite number of digits. In a “precision” (rounding) of 1: π=3; in “precision” of 2: π=3.1; “precision” of 4: π=3.142; “precision” of 8: π=3.1415927, and so on.
Adjusting to lower precisions is advantageous for achieving faster computations and lower memory requirement, but with lower accuracy (e.g., 3*6=18 is easier to compute than 3.1415927*6=18.848556, but also less accurate). We can apply a similar, albeit more complex, process to lower the precisions of neural network architectures, which primarily consist of matrix operations.
In most cases, a neural network will be trained in 32-bit floating-point precision, known as fp32. We can then quantize lower precision values to achieve faster computation, lower power requirements, and lower memory when deploying the neural networks on actual hardware. Yet, finding effective mixed-precision quantization configurations is very challenging given that the combinatorial search increases exponentially for each operation in the neural network. For common ImageNet models, this search space can be extremely large. Consider these examples:
- MobileNet-V2, with 116 quantizable operations, has ~10**69 possible combinations
- ResNet50, with 124 quantizable operations, has ~10**74 possible combinations
- ResNeXt-101-32x8d, with 244 quantizable operations, has ~10**146 possible combinations.
By comparison, the number of stars in the Milky Way is estimated to be ~400 billion, which is ~10**11, meaning that for mixed-precision quantization of ResNeXt-101-32x8d, one would have to search the equivalent of 150 Milky Way galaxies to find a set of optimal configurations.
NEMO
To tackle these challenging combinatorial search problems, our team at Intel Labs developed a novel method: Neuroevolution-Enhanced Multi-Objective Optimization (NEMO). NEMO’s key innovations include an integrated framework for leveraging different types of data representations that describe the underlying problem. Classical multi-objective search, for example, relies on a parameter-free approach. In a search requiring 100 different decisions, the algorithm directly outputs 100 different numbers. However, this representation approach may not be the best choice for every problem, particularly for neural networks architectures.
In our study, in addition to applying traditional search methods, we created a graph-based embedding for neural network models and applied Graph-Neural Networks (GNN) to analyze the graph embeddings effectively. GNNs are neural networks that efficiently process graph-based data by aggregating information across various neighborhoods in graph input data. By integrating GNNs into the NEMO search framework, we can exploit neighborhood dependencies in the inherent graph-based structure of the neural network inference workloads. Our paper shows that the addition of graph-based representations is critical to NEMO’s ability to address the vast search problem presented in mixed-precision quantization.
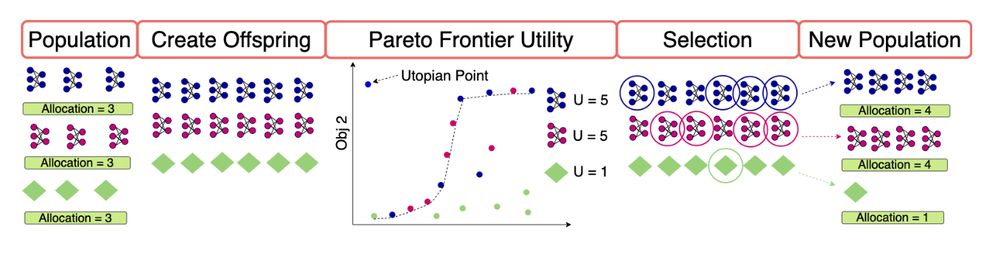
Figure 2. General flow of NEMO: First, we create a population with different representations; in this case, three representations (called species) of size three are used for a total population of nine. One species is a traditional search method shown as green diamonds. The other two are GNN-based species shown in magenta and blue. We then apply mutation and crossover methods including classical search and neuroevolution techniques to create offspring, thereby doubling the size of the population. Subsequently, we create the Pareto frontier based on the available solutions and compute a utility metric for each species. In this illustration, the utility represents the number of solutions in the Pareto frontier. Finally, we calculate the allocation of each species based on the utility metric mentioned above and select the members of the population that transfer to the next generation.
In our paper, we illustrate the mathematical descriptions of the utility functions and allocation methods, as well as relevant details defining the graph data structures and the types of GNNs we created as species for the NEMO optimization.
Results
In our work, we leverage Intel’s OpenVINO toolkit, specifically the Neural Network Compression Framework (NNCF), to compress a target ImageNet workload according to the mixed-precision configurations determined by NEMO. We then report a Pareto optimal set of these configurations. As NEMO continues to improve from generation to generation, the Pareto optimal set continues to evolve to better and better solutions. At the end, we achieve ~8.0x memory compression and ~5.0-8.0x theoretical compute reduction on MobileNet-V2, ResNet50 and ResNeXt-101-32x8d.
Given the promising results of NEMO on mixed-precision quantization, we plan to apply our method to additional neural network compression challenges, as well as general multi-objective problems that involve large combinatorial search spaces. Some examples of these problems include, but are not limited to, automated design of hardware systems and automated design of material systems that make up the underlying hardware.
For more details, please read our paper.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.