- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
From Wikipedia
In 1966 the FORTRAN people have chosen the sequence of arguments (y,x) although there is no doubt that they address the (x,y)-cartesian plain and although the +x-axis plays the prominent role of the so-called polar axis in that all (x,y)-arguments on it are intended to yield the result 0. Most probably their choice is a reminiscent of the sequence in the quotient y/x, although they could equally well have thought of x−1y.
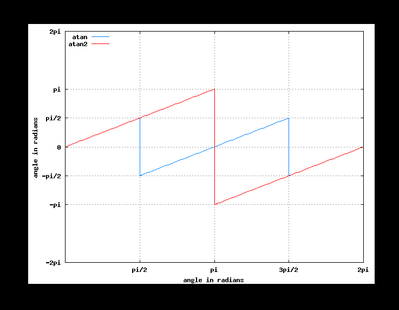
If I measure the angle theta from polar coordinates as positive for a CCW rotation from the X axis, why does one think that the 1966 programmers used -pi to +pi in such a crazy fashion.
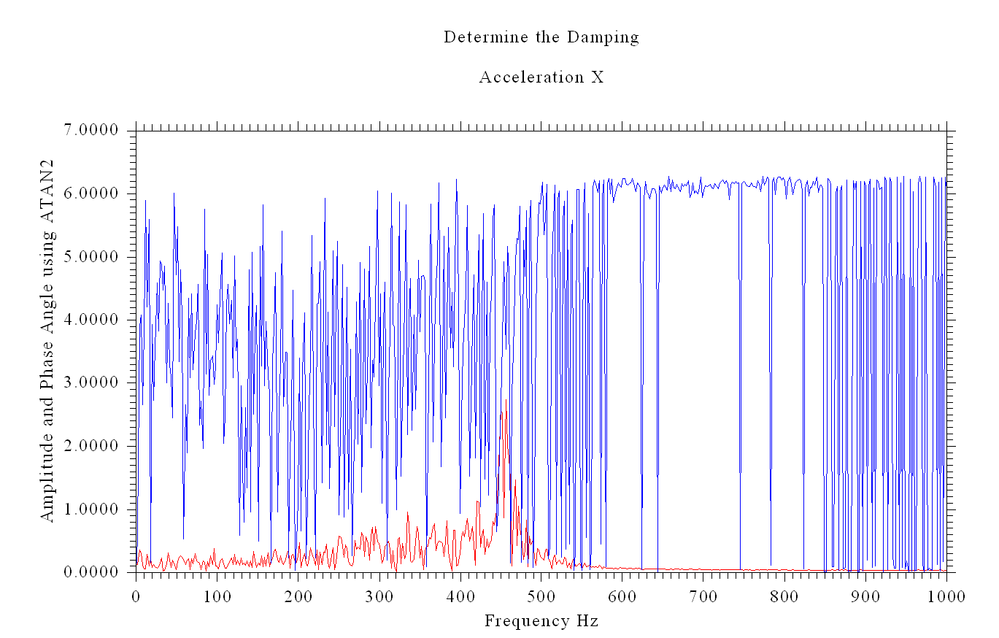
I was plotting some stuff from MKL using a FFT. The ATAN2 fixed to be pure polar when drawn makes more sense. See graph. But when drawn as ATAN2 hides the concept behind the data.
The interesting challenge is that someone made a decision in about 1965 and we live with it forever, the joys of humanity.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I use atan2 all the time the -pi, pi range makes perfect sense to me! Lets face it in any specific usage you mighty want to range things differently but a couple of your own utility functions takes care of that. Whatever range was used for a continuous rotation there is always going to be a cyclic discontinuity ever 2PI that needs to be considered. But yes Fortran was the first language to address the issues with arctan by the creation of atan2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
True, but the definition of polar suggests continuously increasing theta, I can see why they did it, I was interested that a decision made in committee in 1965 sits with us forever, I know it is easy to fix, it is just an interesting point to ponder on.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I'll note that you can now say ATAN(Y,X), which is the same as ATAN2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I didn't know that is that an f2018 thing or much older?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I dragged out my old Fortran manual Microsoft 1991, version 5.1 and it is not in there, it is the original atan function.
In the front of my manual is a Intel Forum post from Steve Lionel where he tells me how to set up the MKL settings, the date is faded, but it appears to be pre 2000. He looks young in the picture.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@JNichols wrote:In the front of my manual is a Intel Forum post from Steve Lionel where he tells me how to set up the MKL settings, the date is faded, but it appears to be pre 2000. He looks young in the picture.
Probably from 1999 - that's the picture I used for a long time (current one is from 2014 - I should probably replace it, but I don't have a lot of pictures of myself.) But if it's an Intel forum post, the post itself will be 2002 or later.
Edit: New avatar is from 2018.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@andrew_4619 wrote:
I didn't know that is that an f2018 thing or much older?
2008.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
JNichols wrote: "... why does one think that the 1966 programmers used -pi to +pi in such a crazy fashion"?
The Wikipedia article on atan2, which you alluded to, contains the straightforward answer, where it says "The function atan2 computes the principal value of the argument function applied to the complex number x + yi."
The notion of principal value is at least two hundred years old, so we should not blame the "1966 programmers".
Another page , definitely centered in mathematics, contains a definition of the principal value.
As Andrew has pointed out, a convention that is generally favored may appear less than ideal in some specific application area. That does not make it "crazy".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You are of course absolutely correct, my choice of words was poor. Let us say they had an interesting choice to make. Wikipedia notes the two alternatives, interesting is the order. Clearly in a meeting somewhere the function was proposed and the range value set, I think it is interesting to take the 2pi step at pi, rather than 0, in real terms of math it is irrelevant, in drawing graphs it makes an interesting choice, sometimes in looking at a language one asks why.
We are human and we have opinions, a part of life is taking sides on opinions. Fortran is not perfect, but it is more perfect than most. A better function would have been ATAN3(x,y,i) where i is an int that tells you the output range, then we do not have to fool with a stack of if statements.
And place the X and Y in the more mathematically logical order.
-
Principal value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Given that Fortran has evolved over six decades, the probable result of digging up the answer to your "why...?" would be so voluminous and disjointed that you would not finish reading the report even once. Even if I did read it, I would forget, and would have to look up the function in a reference manual, whether a hard copy, PDF/HTML file, or hover help.
When you say, for example, "A better function would have been ATAN3(x,y,i),..", I have a problem. You do not advance any explanation of why you think so; therefore anything else that you write that depends on my accepting your declaration of "better" will probably be skipped over, unless you are a known authority on the matter.
You can look at how C# and Java define the corresponding functions. For C#, the documentation shows that the Fortran conventions are followed. In particular, the function argument order is "y,x", rather than "x,y".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Considering that sin and cos functions return -1:1 (or 0:2pii), it would not be unreasonable to expect atan... to have returns of similar nature.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Re: sin and cos functions return -1:1 (or 0:2pii)
Yes, but the sin function also returns -1:1 for -π/2 to +π/2.
Indeed, in Fortran the range of ASIN() is -π/2 to π/2, whereas the range of ACOS() is 0 to π . These ranges could also have been chosen differently. Australia's nickname could have been "Up Above".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Perhaps a different range could have been agreed upon, but this coincides with the common mathematical convention.
One could also say that as the square of both abs(x) and -abs(x) is x**2, the square-root function should return -x. Equally valid, but at odds with mathematical conventions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have served on very many standards committees, I have no further lifetime interest in offering new standards.
ATAN and ATAN2 are perfectly good base functions, they do miss the first range 0 to 2pi offered in wikipedia and which I was taught in Pure Math at ANU in the 1970s. Again the personal preference of the lecturer and the textbook.
The people on this service are of two types, absolute FORTRAN experts who could look at the proposed interface for ATAN3 and understand exactly what is proposed, the observation that I prefer X, Y to Y, X is interesting, as mecej4 notes there are several reasons to stick with the current method, in a standards committee it would be discussed and voted upon. If I was on such a committee, I would find mecej4's arguments persuasive. If we dug out the minutes for the original committee I am sure we would find these things discussed. The second type are beginners who need simple ONEAPI type questions answered. I am amazed at the amount of time the key players here offer these people. You are to be praised.
C# is Microsoft's version of Fortran. I can take a Fortran program run it into C# - run the compiler and make minor simple changes to get it running. If you want to use advanced C# features, they can change so quickly, stuff from last week at version 0.9 may not run on 1.1. There is not this type of support board, there is one, but the response times are much slower.
The graph above shows the advantage of graphing from 0 to 2pi for the phase angle, it is much clearer, I know I tried both of them.
ATAN3 is syntactic sugar, it offers nothing over ATAN2, just a slight simplification in the use.
LISP is a language where you very rapidly move away from the simple basic language and develop routines. It would be nice if Fortran was quite that nice.
We should be able to chat about simple things, without to much ire.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page