Drawing circles in Fortran

[JohnNichols]

 !-------------------------------------------------------------------------------------------------------------------------------
    !
    !
    !
    !-------------------------------------------------------------------------------------------------------------------------------

    subroutine rgbimage_draw_circleA(this,x0,y0,radius,color)

    implicit none
    class(rgbimage),intent(inout) :: this
    integer,intent(in) :: x0,y0,radius,color
    integer :: x,y,err,L,count

    x = radius
    y = 0
    err = 1-x
    count = radius

    do while (x >= y)

        do 200 L = 1,3

            this%input(L,x + x0,y+y0) = this%colors(color,L)
            write(*,*)x,y
            this%input(L,y + x0,x+y0) = this%colors(color,L)
            write(*,*)y,x
            this%input(L,-x + x0,y+y0) = this%colors(color,L)
            write(*,*)-x,y
            this%input(L,-y + x0,x+y0) = this%colors(color,L)
            write(*,*)-y,-x
            this%input(L,-x + x0,-y+y0) = this%colors(color,L)
            write(*,*)-x,-y
            this%input(L,-y + x0,-x+y0) = this%colors(color,L)
            write(*,*)-y,x
            this%input(L,x + x0,-y+y0) = this%colors(color,L)
            write(*,*)x,-y
            this%input(L,y + x0,-x+y0) = this%colors(color,L)
            write(*,*)y,-x

            if(count >= 3) then
                this%input(L,x + x0 - 1,y+y0) = this%colors(color,L)
                write(*,*)x-1,y
                this%input(L,-x + x0 + 1,y+y0) = this%colors(color,L)
                write(*,*)-x+1,y
                this%input(L,-x + x0 + 1,-y+y0) = this%colors(color,L)
                write(*,*)-x+1,-y
                this%input(L,x + x0 - 1,-y+y0) = this%colors(color,L)
                write(*,*)x-1,-y
            end if

            if(count >= 2) then
                this%input(L,y + x0,x+y0-1) = this%colors(color,L)
                write(*,*)y,x-1
                this%input(L,-y + x0,x+y0 - 1) = this%colors(color,L)
                write(*,*)-y,x-1
                this%input(L,-y + x0,-x+y0 + 1) = this%colors(color,L)
                write(*,*)-y,-x+1
                this%input(L,y + x0,-x+y0 + 1) = this%colors(color,L)
                write(*,*)y, -x+1
            end if


200 end do

    count = count - 1
    y = y + 1

    if (err<0) then
        err = err + 2 * y + 1
    else
        x = x - 1
        err = err + 2 * (y - x + 1)
    end if

    end do

    return

    end subroutine rgbimage_draw_circleA


    !-------------------------------------------------------------------------------------------------------------------------------
    !
    !
    !
    !-------------------------------------------------------------------------------------------------------------------------------

    subroutine rgbimage_draw_circle(this,x0,y0,radius,color)

    implicit none
    class(rgbimage),intent(inout) :: this
    integer,intent(in) :: x0,y0,radius,color
    integer :: x,y,err,L,count, i, j

    x = radius
    y = 0
    do 100 i = -radius,radius,1
        do 150 j = -radius,radius,1

            do 200 L = 1,3

                if(abs(i)+abs(j) .lt.  then
                    this%input(L,i+x0,j+ y0) = this%colors(color,L)
                endif

200 end do
150 end do
100 end do

    return

    end subroutine rgbimage_draw_circle

One of the things you need with a graphing package is circles. The circles are most useful plotting points on Xy Scatter Plots.  I borrowed one, here called circleA and it gives you a nice circle without the center filled.  But it can get hard to see if the circle is small and done in a light color, say yellow.  

I was playing with filling in the center and it occurred to me there was a much simpler way.  Anyway aside from the numbered do's it works a treat.   I wonder which is faster.  

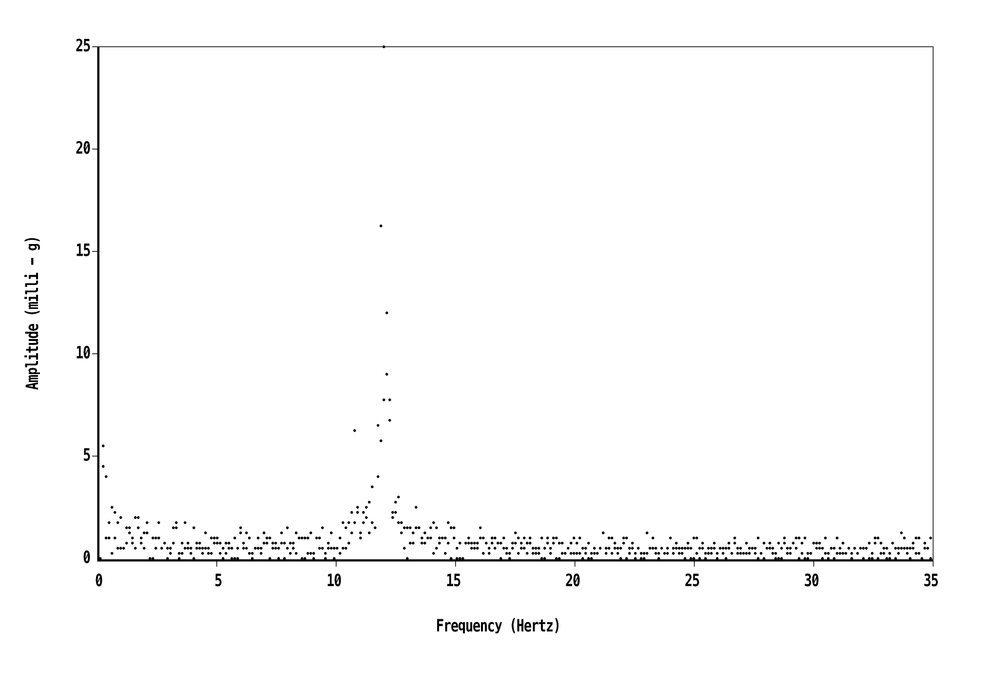
Turning the text sideways was fun.  This is an FFT for a timber beam. 

[JohnNichols]

The interesting question is now the Fortran Translation code for turning a pixel letter through any angle.  

[mecej4]

Using the center, centroid or some suitable reference point of the bitmap of the character as origin, represent the dots by complex numbers, and multiply the array of dot coordinates by cos φ + i sin φ. The real and imaginary parts of the results are the x and y coordinates of the rotated image.

[cryptogram]

I was playing with an approach that uses polar coordinates and parametric equations to map pixels from a pattern into a rotated

rectangle

which works ok for 90, 180, 270 degree rotations, where the pixel mapping is 1 to 1.

Doesn't work quite so well for other rotations, where you get something like this

The issue, I suspect is that sometimes I really need to have one pixel from the pattern light up more than one

pixel in the result.  Instead of remapping just the location of the center of the pixel, might need to figure out

the locations of the corners and see where each of them land.

[jimdempseyatthecove]

There are a few problems with bitmap (pixel) image rotations. Firstly the initial bitmap is a coarse approximation of the original image. Assuming the pixel X and Y unit (visual) lengths are the same, then any rotation not an integral multiplication of 90 degrees will require weighting redistribution of the "from" image into the "to" image. This will introduce additional error into the "from" image over the original approximation. Thus, if you do not keep the original pixel image around (original approximation), should you subsequently rotate the rotated image, the errors accumulate with each rotation.

The best (image preservation) IMHO would be

Given an original bitmap (assuming you do not have a vector based character set). Convert the description (bitmap) of the image representation into either circular or spherical notation with the center point in the center of the pixel and with the radii equal to 1/2 the pixel unit length. Call this a sprite. Then preserving this (or re-computing this when needed) representation you can rotate the sprites about a chosen reference point (either 2D or 3D). Then produce the new bit map from a weighted intensity based on the proportion of the area or volume of the rotated sprite residing in said pixel.

Jim Dempsey

[JohnNichols]

Thank you for the replies. One of the standard algorithms triples the number of pixels, does a series of stretches in the X and Y direction and then downsizes. 

Yes, the pi/2 angles are all trivial, it is a matter of swapping the x and y, but I think that if divide each pixel into 4 sprites, so I have a [0,0,0,0] or [1,1,1,1] matrix for each 0 or 1 and then rotate each one and assign each sprite number to the closest sprite, just use an addition function as some may overlap,  and then decide on the 0 or 1 based on the number of sprites turned on in each pixel.  

Luckily with ASCII you have the original bit maps.  Actually you could write out the rotated bit maps to a text file and then just load it.   I will try 45 first. 

We have the advantage that Fortran is fast. 

There is an excellent article on supercomputer development over the period 1940 to 2020 in the Maximum PC magazine.  It has a lot to say about the place of Fortran.  They also mention that John v N, grabbed ENIAC to do bomb calculations, the punch card deck was 1 million cards. It could do 4000 calculations per second.   It also mentions that Cray was once convinced to give a talk somewhere.  He did not speak much.  Anyway the talk went well, and the moderator asked for questions, no questions were asked. Cray leaves. The moderator walks over to a bunch of attendees, and says 'Why no questions?"  Reply, "One does not ask God questions."

I laughed.  

[JohnNichols]

The routine checks the length of a integer above 0 and set the correct print mode, but why does the 4th and the 7th line not cause an error as they are both true? 

if(num .lt. 10) then
        KVG%flag = 1
        write(kvg%A,'(I1)')num
    else if(num .ge. 10 .and. num .le. 100) then
        kvg%flag = 2
        write(kvg%B,'(I2)')num
    else if(num .ge. 100 .and. num .lt. 1000) then
        kvg%flag = 3
        write(kvg%C,'(I3)')num
    else if(num .ge. 1000 .and. num .lt. 10000) then
        kvg%flag = 4
        write(kvg%D,'(I4)')num

    end if

[cryptogram]

I would guess that line 4 was meant to end with  .lt.100 instead of .le. 100.   This actually matters

when only when num = 100.  In that case it will go through lines 5 and 6, and since num won't fit in the

(I2) format,  kvg%B will end up with  holding **.  Not an immediate error, but perhaps problematic later on.

Since it falls into 5 and 6, the subsequent else if will prevent it from running 8 and 9.

[jimdempseyatthecove]

In addition to line 4 .le. error posted by cryptogram...

write(kvg%numAsText,'(I0)') num ! left justify into character(len=4)
kvg%flag=lentrim(kvg%numAsText) ! later use kvg%numAsText(1:kvg%flag)

IOW replace the nested IF and four character variables, used to build one of four character variables then, presumably later, used to select one of four character variables, with a single character variable and a length to be used later.

Jim Dempsey

[cean]

Is this to generate an image file?