Floating Point Consistency

[Kantor__Baruch]

Hi

I'm upgrading a CVF application that relies heavily on single precision floating point calculations.

I'm using the "Enable Floating Point Consistency" and "Extend Precision of Single Precision Constants".

Currently I create IA-32 Fortran DLL on XE.

From comparing the results of the CVF and XE versions I see that the CVF application is more precise.

It looks like in CVF there are more significant digits (or half digits).

I've read previous posts regarding Floating Point Consistency, including referred documents and presentations.

I've tried all possible combinations of the Fortran Floating Point Settings and still can not recreate precisely CVF results.

Will be grateful for any insight on this.

Baruch

[Steve_Lionel]

First, read http://sc13.supercomputing.org/sites/default/files/WorkshopsArchive/pdfs/wp129s1.pdf

CVF did not use SSE instructions for floating point - it used the X87 registers and instructions. Sometimes this would keep intermediate results in "higher than declared" precision, leading to the effect you noticed. It was not something you had any control over, though.

If you need better precision then you should do key computations (if not all of them) in a higher precision data type/

[wtstephens]

If I want "reproducibility" of an old CVF (DF compiled) .EXE program then I would first want the same Intel chip at the same MHz speed?

In my current case I have tried Pentium 3 chips at somewhat different MHz speeds, and they do not reproduce the exact same calculations. 

So I am gathering that I should try next the identical Intel chip, which may get me there? -- because it may recreate the data alignment or some such?

The .exe was compiled with "-tune:host" I am fairly sure.

[mecej4]

It does not make sense to me that you program using  single-precision and then complain when the results are not sufficiently precise. With x87 arithmetic, you might have obtained better precision in intermediate results, and perhaps better precision even in some final results, than with single-precision SSE2 arithmetic. The more important question: do you get sufficiently accurate results using double-precision SSE2 (or more recent) FPU arithmetic?

[Kantor__Baruch]

Steve,

I've read this presentation but it does not include the point you've raised ragerding the X87 instructions.

Your explanation seems to perfectly support my findings. I guess I cannot make XE use X87 (?)

mecej

Tho code I use was written 30 to 40 years ago with tens of thousands of lines.

To change it to double precision will not be a straightforward task.

Thank you!

[mecej4]

Kantor, Baruch wrote:
 Tho code I use was written 30 to 40 years ago with tens of thousands of lines.

To change it to double precision will not be a straightforward task. 

In that case, see how far the compiler's /real-size:64 will help you. From the documentation for the Intel Fortran compiler:

Makes default real and complex declarations, constants, functions, and intrinsics 8 bytes long. REAL declarations are treated as DOUBLE PRECISION (REAL(KIND=8)) and COMPLEX declarations are treated as DOUBLE COMPLEX (COMPLEX(KIND=8)). Real and complex constants of unspecified KIND are evaluated in double precision (KIND=8).

[Kantor__Baruch]

mecej4

I wish I could use this option but I'm limited with structures of existing binary data files and communication ICD's and API with other programs that I can not change.

[Steve_Lionel]

The paper doesn't specifically address X87 - the initial audience for the paper wouldn't be caught dead using X87 floating - but it does fall under instruction set differences (not to mention compiler differences.) Your situation is one I have seen before where a particular result is "accepted as correct" and then no deviation is allowed. In the end, especially given the distance in time and hardware, you may have little choice but to either accept the newer results or put in the effort to update the application so that it declares the precision it requires.

[Kantor__Baruch]

Steve,

My problem is to justify buying new compiler licenses and then spend hundreds of working hours just to get the same (correct) result.

I've tested some specific calculations and no doubt: CVF was much more precise in single precision arithmetic.

We are commercial company and the managers are not ready spend time and money just to use 2018 software and not 1998...

CVF worked for 20 years and will continue to work for another 20 years.

Thank you

Baruch

[Steve_Lionel]

CVF was also inconsistent - you had no control over when an expression was kept in extended precision and when it was rounded to single. I disagree that the results were "correct". How exactly did you determine that they were correct - did you do extensive numerical and computational analysis on each calculation? Or did you look at the results from CVF, say they "looked right", and called it a day?

If CVF continues to work for you, that's fine, but the development environment is completely unsupported on modern Windows versions.

[Kantor__Baruch]

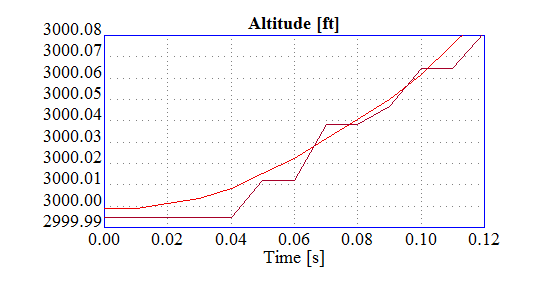
You are right of course that when the computation are complex the precision on the X87 single is not consistent - depends of the usage of the X87 registers.

My software is made of large number of quite simple formulas so it is less relevant to me.

I took some atmospheric formulas, integration and linearization routines and converted them to double precision.

The CVF results (single) were much closer to double. In system linearization the differences were rather large.

Looking on state variables like altitude it is obvious that the the granularity of the smallest changes in CVF are much smaller than in XE.

Thank you

[TimP]

The use of extended precision in CVF should be mostly matched by 32-bit ifort with setting of IA32 instruction set.  As these applications are normally run with x87 precision set (by default with CVF and ifort) to 53 bits, it is equivalent to promoting intermediate calculations with REAL(x,REAL64) or, in F77, dble().  As Steve pointed out, you have no control over where CVF or ifort do this automatically for the "IA32" target,and ifort may not exactly match CVF. 

If you wish to take the trouble, you may insert explicit promotions in your code for each expression involving 3 or more operands.  Due to the mixed data type promotion rules of Fortran,  one insertion of dble() will take care of a 3 operand expression in some cases (like A*REAL(X,REAL64)+B). Of course, this REAL64 (if you don't define it yourself) depends on USE ISO_FORTRAN_ENV, which ifort has supported in recent years.  You could make up your own named module or internal function to abbreviate the verbose REAL intrinsic while improving future portabiity compared with DBLE(). Then you could expect portability to Intel64 targets.  It may be necessary, or at least helpful, to declare all local scalar variables as REAL(REAL64).  REAL(8) would work with ifort compatible compilers, but it is poor style.

When using simd instruction sets, which you probably are doing, as ifort defaults to /arch:SSE2, mixed single and double precision are likely to reduce performance, hence the preference of previous replies to suggest full doube precision.

[Kantor__Baruch]

Tim,

I've considered such options but if I'll get the budget I will go all the way to double precision calculations while keeping ICD's and API intact.

Above you can see the diffrence between the two compilers. The XE results were with arch:IA32 settings.

[jimdempseyatthecove]

@wtstephens do you see a difference when running the same .exe file?

.OR.

are you seeing a difference when compiling the program using a different compiler?

The older environment, the then compiler, may have been using (in places) the FPU instructions.

Whereas the newer compiler may be using all SSE/AVX/AVX2/AVX512 instructions.

The FPU has internal 80-bit (ten byte) floating point temporary registers.

Whereas the SIMD instructions are all 64-bit (eight byte) registers (except when using Fused Multiply and Add instructions which has a few more bits preserved between the multiply and add).

Jim Dempsey

[wtstephens]

I have the exact .exe file (from the year 2004) and corresponding data files.

I can also re-compile from source code and get an EXE file that has only 8 bytes of differences (using the same CVF "DF" commands).

Using desktop Pentium 3 chips of 933MHz and 1GHz with the original EXE and data files I do not get matching output files versus the original output files.  Those chips output files do match each other, but do not match the original output files from the mobile Pentium 3 850 MHz output files.

I have ordered a desktop 850 MHz Pentium 3 to try that (assuming it will plug into the same Socket 370 as the 933 MHz or 1 GHz -- despite the slower Front Side Bus of 100 MHz versus 133 MHz).

Should I expect that I will eventually need to try a mobile chip?

[wtstephens]

After a great deal of effort, I was able to get the old 2004 .EXE program (which was compiled with CVF "DF"), and the old data files, *and* the correct input parameters to exactly reproduce the old floating point output that I wanted. Yay! 

It worked using a 750MHz mobile Pentium 3 chip, even though the original calculations were done using an 850MHz mobile Pentium 3.  These laptops I bought on eBay are 25 years old! Cheap though, like $50 each.

Along the way, I do now believe that all the Pentium 3 chips that I now own (again) might be used to reproduce the calculations -- and I may try to verify that over the next couple of weeks.  All of this is under old Windows 2000.

Also, I will be trying to get the same results using the 'virtual CPU' that VMWare Workstation v17 has in its Windows 2000 support, which is of course not the host machine's Xeon 12-core, but a 2-core VM that is compatible with Windows 2000.

[wtstephens]

The VMWare Workstation running Windows 2000 will exactly reproduce the Pentium 3 calculations.

This is using CVF 6.6A <-- yes, "A".

At this point I am trying to figure out how that CVF and gfortran (yikes!) can get different answer to dividing the very same REAL*8 values -- the equation is result = (1.0-x)/(1.0+x)

The results differ by just a little, way out there at the 16th digit.

There are so many gfortran architecture compile options -- anyone have a formula to mimic old CVF???

[andrew_4619]

I find it quite hard to understand why you would want to replicate exactly of an ancient compiler and processor.  What is the ultimate objective? Why would a delta in the 16th sig fig be of any importance?

[wtstephens]

My first objective has been to re-build and re-run old code in order to match specific source code versions to specific old input and old output data sets -- an exact match is proof of the set: "old-Data + old-Code/Compiler --> old-Output".

It is a very slow process.

It has been helpful to use modern compilers and chips to speed up the process -- execution is around 20X faster (Xeon 12-core).

In order to get the modern stuff to closely mimic the old has required looking at intermediate calculations. Some of these calculations skirt very close to zero or asymptotes.

I agree that the 16th sig figs are in "rabbit hole" territory, but some are in the 12th digit.

Successes so far have been in adding double-precision changes here and there in the code.

[jimdempseyatthecove]

Have you  seen: https://en.wikipedia.org/wiki/Pentium_FDIV_bug

Jim Dempsey

[wtstephens]

Thanks.  Looks like that Pentium bug was in 1997.  My original Pentium 3 system was bought in late 2000.

A matching Pentium 3 850MHz is (hopefully) arriving on Monday for me to try.