- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Well I have been playing with an interesting Fortran program that looks at Primes. It is a lot of fun, and sometimes it is a heartbreak.
I wanted to connect the Fortran program - Intel of course, one is reminded here of the famous lines between Tom Hanks and Ian McKellen in the Da Vinci code to, a database in the cloud.
It should have been easy, but it failed. Of course I blamed myself for the failure.
About a week ago I tried Filezilla to connect to the cloud system, I have done it for years with no problems, but it failed.
Step 1 - spend several days trying all options and finally use my phone's wifi hotspot, worked first time.
Step 2 obviously the router/modem from the internet provider has some problem, never had a well known brand fail like this.
Step 3 - day 1 - charming chat with tech person located it seems in some foreign land. Told fixed, was not.
Step 4 day 2 - much longer chat with another tech person who assured me they had fixed the problem, before I could check they hung up. Much chaos and laughter.
Step 5 day 3, another very long chat with a another tech person who had a heart attack on the call when I asked for the supervisor, she got very upset. I said ok. After an hour, she said get a tech person to arrive in person. Arranged for 2 days hence.
Step 6 day 5 - waited patiently till 5pm for the tech guy to arrive, finally arrived 6 hours late, said he was a bit busy. I showed him the problem, he laughed and said did I expect him to fix it, I said well I jolly well hope so, he said:
1. This is an engineering problem and no one talks to the engineers => NO ONE.
2. It is probably related to the new Chinese router modem that the company has made in China and every one has to use, he said buy your own.
3. I said ok, but why did the old one work.
4. He said I have one in the truck, he got it and nicely installed it against company policy.
5. Two seconds later it all worked.
6. I thanked him and offered him a coke, he said no and left.
Of course the new router broke the wifi, today, day 6 I looked at experimental nuc in garage, darn I need to connect it to the wifi. Pull it into the house, connect to all the stuff on a home computer,
1. Daughter is upset I turned on the lights and spoiled her gaming
2. The nuc said cmos battery failed,
3. Took several goes to get it going.
4. Looked up instructions to replace, another engineer has placed the cmos battery on the bottom of everything. So a long look at youtube.
5. The two small screws on the motherboard are impossible to get to without a lot of torture.
6. The adhesive is so strong I pulled a part of the board trying to get it off, and finally used my handy dandy pocket knife with two blades.
7. Instead of a nice easy slip in sleeve, it is 15 dollar part from Amazon, the Intel site even says buy from Amazon or a online retailer.
8. Ordered part, computer in pieces for three days. The NUC instructions say disconnect the aerial cable - it is soldered on.
The world is a highly connected place and Internet providers and engineers are strange, I am an engineer and some of my brethren are smartly insane designers.
Back to the primes and Fortran.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The WiFi antenna is NOT soldered on, but the connector is extremely fragile. Grasp it with your fingers and pull straight up.You also have to make sure that the card you buy supports the chipset in the PC - I ran into this lately when replacing the card in my laptop. First, I managed to damage both the antenna cable connector and the one on the current card. I replaced the antenna (with its wires) and then found that the card I had ordered required a more modern chipset than I had. Eventually I ended up with a combo that works.
This is not Intel-specific - all of that form factor of WiFi card is like that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I was afraid to pull any more wires, so I got it out will all of the wires in place except one.
The NUC's are an amazing piece of engineering and a joy to work with, compared to everything else I own. But it is still fun to poke fun at engineers, the people who fix unbroken things.
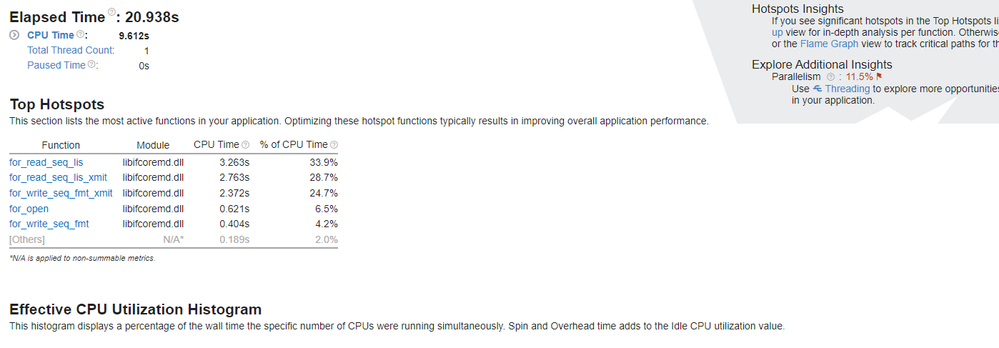
I just got my prime program running under profiler, and James is correct I need to now add openmpi.
does the for_read_seq = means Fortran read routine?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Primes:
Are interesting.
If I load the primes into an array in Fortran on Windows at about 1 million I run into the 2GB limit, give or take a few hundred thousand.
You cannot load the primes, so this makes the programming interesting.
Intel Fortran can have a number up to limit = 9223372036854775807, which if I seek the primes to this number, I have enough computers that just letting one stump along, is not a problem, by the time I have searched 100,000,000 numbers I am 1e-12th of the way there. As 5807 is a prime number then the limit is likely to be prime.
The RSA system operates at composite N of 1e308, which means the likely primes p and q are in the region of 1e154.
On reading the RSA manual, it is not fully guaranteed that p and q are prime. For reasons that are not fully obvious the Intel Random number generator tends to pick p and q close together, more often than far apart, but far apart is much harder to crack time wise.
The famous function pi(n) is simply a third order polynomial - with an r2 of 1. pi(n) fits the middle of the series, it is just as interesting to fit the upper and lower limit, so there are 25 less than and including 97, 100 is just close to the midpoint of the 25th set or composites.
Anyway it is just some xmas fun while my daughter does her thing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Your post confused me. Your are searching for primes up to the maximum 64 bit unsigned integer but "at about 1 million I run into the 2GB limit" but 1 million x 64 bits is only 8MB. Are you saving them as decimal text?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
My apologies,
1. There are a lot of programs on the web that find primes. Most that I looked at use an array to hold a true false value to determine if the array element is a prime.
2. These programs run into the limit size on a Windows program of 2GB as the array grows. The array does not have to be very big in prime terms to be of little real use.
3. I wrote code to only look at one number at a time and store the results on an SSD, which for the early work is fast enough.
4. Now as I look at a much greater number of primes, over 10 to the ninth power on my core i3 at the moment, you need to look at ways to reduce the time to find a prime, for the interesting work one needs a list of primes. So one goal is to determine how fast you can generate primes, and save your work so a power interruption, unforced computer reboot, (today I found out if you unplug the very old DVD writer I have from the NUC it reboots the NUC. I will not do that again"), does not stop you going forward.
5. Reading on OPENMP and pondering what JD commented, it appears to me I have looked at most of ways to speed up the algorithm running in a single thread, but I think I worked out how to make it run in say 3 of the 4 cores on the NUC i3.
6. The other problem is the NUC only has a 150 GB of spare space, the program can use a lot of space to store results. (Two passes on the prime finder using 2 and 3 as the mod values requires a 70GB file to hold the remaining numbers to 90 x 10 E9. Finding an efficient way to store the numbers would help, I am sure someone has invented one.
7. I read a statement on primes before xmas, that said there was no "known" way to solve a particular problem, "but someone had added that one may exist, it just not known. I was driving with my daughter and in thinking about the primes I saw a pattern, turns out the pattern is useful.
8. I had no children at xmas and I thought it would be fun to look at it.
9. Our perception of primes is that they are quite dense, but as you get to the outer reaches of the prime system they are rare and follow a mathematical pattern in their own space. It is a series of "functions" for want of a better term and the primes are the zeros in the functions. One is the absolute zeroth prime.
10 The program to answer the interesting question has been much harder, but also a lot of fun.
But xmas is over and really I have other things to do. But one's training in using DOS and 640k helps with current limit issues.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@JNichols wrote: "Intel Fortran can have a number up to limit = 9223372036854775807, which if I seek the primes to this number, I have enough computers that just letting one stump along, is not a problem, by the time I have searched 100,000,000 numbers I am 1e-12th of the way there. As 5807 is a prime number then the limit is likely to be prime."
The second sentence is wrong and without any basis. Would you claim that 1729 is likely to be a prime because 29 is prime?
The number under investigation is the (composite) Mersenne number M63. Theorem 2 states that if Mn is prime, n must be prime. Your chosen exponent, n = 63, is composite. Thus, M63 cannot be prime. Determining whether Mn is prime for n = a known prime p is, of course, a well known tough problem.
According to this reference, your candidate number has 7 prime factors. Six of those seven, written as base-10 integers, end with the digit 7. The other factor begins with 7. In the candidate number, the digit 7 occurs more often than any other. One of the seven prime factors is itself a Mersenne prime, and has 7 as its last digit, and is the only prime factor that contains the digit 1. (corrections to these assertions are welcome).
Another way of inferring the properties of these numbers is to express them in base-2. Doing so is a quick way to see that M3, M7 , M9, M21 are factors of M63.
Have fun finding the prime factors!
I have to confess to not using any Fortran in formulating this post.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@mecej4 , I must say I love your posts. Thank you for the chuckle on a Sunday morning, before the shower and the first diet Dr Pepper.
You, of course, are correct; you proved the assertion incorrect, which is the point of mathematics.
You, of course, did it without Fortran in an elegant manner, which will please the Pure Math Geeks.
Statistically speaking, there was between a 3 and 7% chance it was prime, depending on where it fell in the primes pattern.
My interest is not in the primes, it is in a statement that has been made that uses primes, I am merely like you interested to see if the statement is correct, I actually believe it is incorrect.
As a side note, I am of course always chuffed when after 100 years, two or three mathematicians will disprove one of the statements in the notebooks, you see modern academics now hunt in packs, if you write one paper you get one unit of credit, if you write one paper, add two friends, and they do the same you get three credits for one credit of payment. We call that capitalism in some forms of economics, a multiplier.
I should have checked of course, but then I would not have had the great pleasure of reading one of your infrequent posts.
So I trust you have a pleasant day.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
>>These programs run into the limit size on a Windows program of 2GB as the array grows.
That size limit applies to statically allocated arrays (and on 32-bit program dynamically allocated arrays).
This limit does not apply to 64-bit dynamically allocated arrays using integer(8) size(s).
>>Finding an efficient way to store the numbers would help
Because you are storing your primes in a file, intended for use to be repeatedly sequentially read (by multiple threads/processes), consider storing/encoding the files as a sequential list of records (number of records grow as needed when adding primes). The records consists of a list of 3-bit nibbles:
1st 3-bit nibble == # nibbles to define the base prime of the buffer
followed by the number of 3-bit nibbles containing the base prime number of the buffer.
The remaining 3-bit nibbles contains the following encoding
1:7 == the delta/2 to the next prime
0 == the following two 3-bit nibbles contain the delta/2 to the next prime
0,0,0 == end of record
Note primes 2 (and 0 if you are so disposed) are not held in the records (IOW 1st prime is 3)
Take for example the number prime numbers below 1000 (168)
Your bitmap would require 125 bytes of storage (1000/8)
The 3-bit nibble format of deltas/2 (with escape sequence)
167 3-bit nibbles + two escape sequences for deltas >7 or 167+3+3 or 173 3-bit nibbles (omitting EOR 0,0,0)
Or 519 bits of storage equals 65 bytes of storage.
IOW file size shrinks by about 1/2.
Note if you INTEGER(3)'s you can hold eight 3-bit nibbles without any loss
Or INTERGER(8)'s to hold twenty one 3-bit nibbles with a loss of 1-bit (which could be used for EOR)
Your screenshot above indicates that file I/O is the limiting factor (as opposed to compute time). This "compression" technique may come close to doubling your throughput.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
>>These programs run into the limit size on a Windows program of 2GB as the array grows.
That size limit applies to statically allocated arrays (and on 32-bit program dynamically allocated arrays).
This limit does not apply to 64-bit dynamically allocated arrays using integer(8) size(s).
------------------------------------------------------------------------------------------------------------
I understand this point, but at some stage you run out of space in memory for the program or on a standard drive C for the data. So, it is simpler to accept this fact and look to the longest term in the number space. In reality you do this on a supercomputer with a very large hard drive not on an old NUC with a core i3 and a 2 TB drive.
In order to make use of this data, you need an ordered list of primes in a file that can be read by any language. The second use is to develop subsets of the primes that follow certain patterns, to use in analysis. The problems of real interest often use random number generators, finding out which generator someone uses and then looking at the statistical properties of the output can help a lot.
The Intel Fortran random number generator on a 0 to 1 scale has a propensity for returning near the center, one RSA system I saw had a lower limit of 4096, thinking that this helped to hide the solution, actually not allowing primes in the 0.4 to 0.6 range on the 0 to 1 scale makes the search a lot harder.
Speed is the only issue here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Because you are storing your primes in a file, intended for use to be repeatedly sequentially read (by multiple threads/processes), consider storing/encoding the files as a sequential list of records (number of records grow as needed when adding primes). The records consists of a list of 3-bit nibbles:
Thanks for the comment, I have not done this sort of stuff before, so I will need to read a bit. Like all experimental work it is a bit of trial and error and listening to experts. Thank the gods for this site.
I really appreciate your thoughts. Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
FWIW
In looking at the list of primes in the range of 0:1000 (you can examine larger ranges), it is noted that the average separation was 5.958. IOW your bitmap would average six 1 bits for each 0 bit (0 being position of prime number). This also means (for this range), the number of primes is approximately 1/6th the number range. As to if this holds for larger number ranges I will leave that as an exercise for you to perform. Or as my college professor would note QED.
For the list of primes in the range of an INTEGER(8), stored in a binary format as INTEGER(8)
9223372036854775807/6 = 1537228672809129301 primes, and if stored as INTEGER(8)
1537228672809129301 * 8 = -6148914691236517208 (oops int64 overflow) bytes
Or about 12,297,828.8TB of storage
Your 1st approach at storage reduction (the bitmap) would require 9223372036854775807 bits of storage
Or about 1,152,921.5TB of storage ~1/12th (bravo)
The 3-bit nibble approach might require 9223372036854775807 * (519/1000)
Or about 598,366.2TB of storage
Or on the order of the capacity of AWS
So the storage is doable, but not practical (at least at this time).
I think the better approach is to figure out how to generate batches of primes in parallel and distributed.
As for RSA, p*q has 1024 bits or 16x the number of bits per prime product.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
For my own amusement I wrote a short simple code (about 60 lines worth) to find all primes up to the max 64bit signed integer (HUGE) (9,223,372,036,854,775,807). It has a feature that you can interrupt it and then restart continuing where you stopped. I was only working in memory, saving the integer(8) primes list as binary data when interrupted. I ran it for a about 4 hours in total and found the first 600 Million prime numbers. Saving those as binary data is about 4.7GB. It is clear that there is a very long way to go and the data storage would kill my laptop at some point well before HUGE is reached. I will note that SQRT(HUGE) is only 3,037,000,499 and the 147,000,001th prime is 3,055,685,063 which is bigger than SQRT(HUGE) so the amount of storage needed to find all the primes is quite manageable, the problem is there are too many primes to save them all.
I didn't try but for finding primes between 3,055,685,063 and 9,223,372,036,854,775,807 could be partitioned into N ranges for N different processors as the tasks do not interrelate, you would just end up with N+1 prime list files but still have ordered prime data.
I also note that using WinRAR a file size for binary prime data is reduced to 1/10th size which gets you 10 time further before the hard drive is full but still not close to a complete list.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the comments.
1. You cannot solve this problem by using standard current mathematical techniques.
2. But the primes are numbers based on three patterns, the 2's pattern, the 3's pattern and all other prime patterns. Each pattern, which for the two and three patterns has a repeat length of four numbers, and a variation that occurs in the third number, the last pattern is slightly longer and relies on the multiples and the powers of the prime, but it is simple.
3. The primes are the zeros of the full pattern assembly.
4. If you watch the primes develop you notice that there is a repeating set of patterns in the last 3 or 4 digits. This allows one to link the last three or four digits on N to a "very" reduced set of primes that fit the pattern in N. Plus N has to be a number that is represented by two primes, this is also a much smaller set.
5. I know this works I can get a RSA cracker working on numbers around a million in very reduced time now. I know I can speed this up significantly, but at the moment I am just interested in the development of the patterns.
6. How to crack the N and find p and q quickly, take the square root of N and search up and down from there, there is a measure you can apply to say - skip x primes as they are not likely. The properties of the random number generator are important at this stage.
7. If I took the main people from here, put them in a hotel in the mountains in France and gave them a few good laptops, I would say in a month they would kill RSA, I have no doubt you lot are that good. The patterns are to simple not to work, the problem is if you look at primes through the sieve you do not see the elegance and the patterns. Find the patterns and the problem is solved, of course they may not exist, but I doubt that, it has been to simple so far.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
>>6. How to crack the N and find p and q quickly, take the square root of N and search up and down from there
That presumption is only true when p and q are approximately equal in magnitude. Knowing that that would be your search pattern, picking primes that vary greatly in magnitude would defeat your search method.
>>4. If you watch the primes develop you notice that there is a repeating set of patterns in the last 3 or 4 digits.
Then I suggest you study the patterns of the product of two primes to see if you can deduce the relative magnitudes of each prime .OR. see if you can determine a cyclical (frequency) to the patterns such that it reduces you search places. i.e. provides hints for optimal search places.
FWIW (as a side note) most/many random number generators, say 64-bit, start with a 64-bit seed, multiply it by a 64-bit odd number (usually prime) to produce a 128-bit product. Then extract the middle 64-bits. IOW omitting the upper 32-bits and lower 32-bits of the product. Reconstituting the original 64-bit numbers (p and q) from this slice of the product is problematic.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Note 1 from JD
6. How to crack the N and find p and q quickly, take the square root of N and search up and down from there
It is not just the sqrt that is interesting, the method to work needs one to reduce the prime set of the search. If you look at primes 2 to 19. The possible N's are
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | |
| 2 | 4 | 6 | 10 | 14 | 22 | 26 | 34 | 38 |
| 3 | 9 | 15 | 21 | 33 | 39 | 51 | 57 | |
| 5 | 25 | 35 | 55 | 65 | 85 | 95 | ||
| 7 | 49 | 77 | 91 | 119 | 133 | |||
| 11 | 121 | 143 | 187 | 209 | ||||
| 13 | 169 | 221 | 247 | |||||
| 17 | 289 | 323 | ||||||
| 19 | 361 |
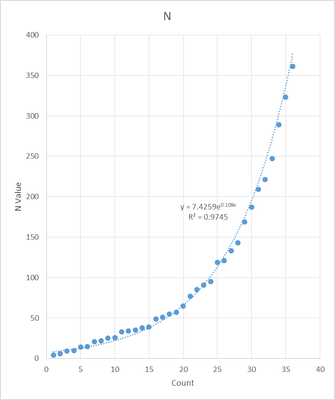
This can be graphed as count versus value - there are no duplicates.
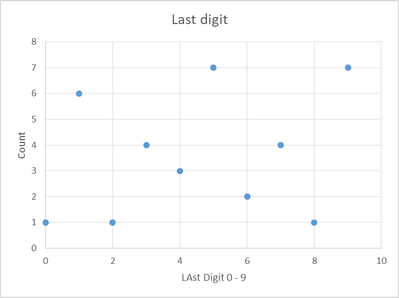
We have to know N, therefore starting from the RHS we know as the first step the last digit. Just using this set we can determine the counts of the last digits in the set. As shown below:
| Bin | Frequency |
| 0 | 1 |
| 1 | 6 |
| 2 | 1 |
| 3 | 4 |
| 4 | 3 |
| 5 | 7 |
| 6 | 2 |
| 7 | 4 |
| 8 | 1 |
| 9 | 7 |
| More | 0 |
So, if the last digit in N - we always should be able to know N, then if N is 4 there are only 3 possible primes of interest 2, 7, and 17. The search size is now 38%. We can then do this for 2, 3, 4, etc last digits.
If I take the sqrt of N then I get say a, so N = a*a, but it would be a fluke if a is the answer, so P > a and Q < a so let P = a+b and Q = a-c
Then
N = (a+b)(a-c)
N = a*a + ba-ca -bc
ba-ca = bc we know a so a = bc/b-c. Therefore b > c,
We can do a lot to reduce our search set. You will never crack it head on, but it is crackable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
MWind2, thanks for that link, which makes for fascinating reading. One startling finding for me was the Lucas-Lehmer and Arndt equivalence:
The Mersenne number M5 = 31 is prime. It is a factor of the integer valued expression
2 cosh(2n-2log(2+√3)) = (2+√3)8 + (2+√3)-8 (= 37634 = 2 X 31 X 607).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The problem as I understand it is:
N = Prime(i) * Prime(j)
Given N, find i and j and thus may be able to obtain Prime(i) and Prime(j) for testing. In simplified terms (assuming an array of primes is available):
do i=1,nPrimes
do j=1,nPrimes
p = Prime(i)
q = Prime(j)
if(p*q == N) return
if(p*q > N) cycle
end do
if(p*q > N) exit
end do
p = 0 ! not found
q = 0
Note, when number of primes to consider is larger than memory, Prime would be a function returning the n'th prime. Where n could be a record number in a file or a starting point for a computational generator.
Now then, assuming you have a database with bins filtered by the last 3 digits (primes < 3 digits assume 0's for leading digits)
BinNum = MOD(N,1000)
do i=1,nPrimes(BinNum)
do j=1,nPrimes(BinNum)
p = Bin(BinNum)%Prime(i) ! or fn(BinNum, i)
q = Bin(BinNum)%Prime(j) ! or fn(BinNum, j)
if(p*q == N) return
if(p*q > N) cycle
end do
if(p*q > N) exit
end do
p = 0 ! not found
q = 0
Binning is a common database practice and would reduce search time.
The problem with this is the BinNum is the MOD(N, 1000) of the product of Prime(i) and Prime(j) contained within the bin. IOW prime numbers can (will) reside in multiple bins. This means the size of the database (#primes) would be larger than the number of unique primes.
Therefore, while at first glance you have a reduction of 1/1000, you have an additional burden of 1.(%duplicates).
Seeing that you have (or can generate) a large number of primes, you could build the database and determine the %duplicates, and thus determine the actual reduction (if any).
Jim Dempsey
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page