Interesting Problem with published code

JohnNichols · ‎01-20-2022

F90 Version By J-P Moreau, Paris. (www.jpmoreau.fr) published a method to calculate the coefficients a and b for the standard Fourier series.

I am taking the a and b symbols from the Kaplan and Lewis textbook.

The code is

! Fourier series routines (version with dynamic allocations)


! analytical function(s) to study:
! -------------------------------
! Note: Exact Fourier coefficients for this periodic function are:
!  an=0 if n is even, -1/2n if n=4p+1, 1/2n if n=4p+3
!  bn=0 if n=4p, -1/2n if n=4p+1, 1/n if n=4p+2, -1/2n if n=4p+3
! ----------------------------------------------------------------
  REAL*8 Function F(x)       !example 1
    real*8 x, PI
	PI=4.d0*datan(1.d0)
    if (x<-PI) then
	  F = 0.d0
    else if (x<-PI/2.d0) then
	  F = PI/4.d0
    else if (x<=PI) then
	  F = -PI/4.d0
    else
	  F = 0.d0
    end if
  END

! Note: Exact Fourier coefficients for this periodic function are:
!   a0=1/pi, an = 0 if n is odd, an = -2/(pi*(n2-1)) if n is even;
!   b1=1/2,  bn = 0 for n>=2.
!-----------------------------------------------------------------
  REAL*8 Function F1(x)      !example 2
    real*8 x, PI
    PI=4.d0*datan(1.d0)
	if (x<0.d0) then
	  F1=0.d0
    else if (x<PI) then
	  F1=dsin(x)
    else
	  F1=0.d0
    end if
  END 

! Function to integrate by Romberg method
  REAL*8 Function FUNC(om,x,flag)
    real*8 om,x; integer flag
    real*8 F, F1
    if (flag==0)  then
      FUNC = (F1(x)*dcos(om*x))       !for an
    else  
      FUNC = (F1(x)*dsin(om*x))       !for bn
    end if
  END

!****************************************************************
!*   Calculate the Fourier harmonic #n of a periodic discreet   *
!*   function F(x) defined by ndata points.                     *
!* ------------------------------------------------------------ *
!* Inputs:                                                      *
!*            ndata: number of points of discreet function.     *
!*            X    : pointer to table storing xi abscissas.     *
!*            Y    : pointer to table storing yi ordinates.     *
!*                                                              *
!* Outputs:                                                     *
!*            a    : coefficient an of the Fourier series.      *
!*            b:   : coefficient bn of the Fourier series.      *
!* ------------------------------------------------------------ *
!* Reference: "Mathematiques en Turbo-Pascal By Marc Ducamp and *
!*             Alain Reverchon, 1. Analyse, Editions Eyrolles,  *
!*             Paris, 1991" [BIBLI 03].                         *
!*                                                              *
!*                           F90 Version By J-P Moreau, Paris.  *
!*                                  (www.jpmoreau.fr)           *
!****************************************************************
! Note: The Fourier series  of a periodic discreet function F(x)
!       can be written under the form:
!                   n=inf. 
!       F(x) = a0 + Sum ( an cos(2 n pi/T x) + bn sin(2 n pi/T x)  
!                   n=1 
! ----------------------------------------------------------------
Subroutine DiscreetFourierHn(ndata, X, Y, n, a, b)
  real*8 X(1:ndata), Y(1:ndata), a, b
  integer ndata,n,i
  real*8 xi,T,om,wa,wb,wc,wd,wg,wh,wi,wl,wm,wn,wp
  real*8 PI 
  PI=4.d0*datan(1.d0)
  T=X(ndata)-X(1);  $xd[$ndata] - $xd[1]
  om = 2*PI*n/T; a=0.d0; b=0.d0
  do i=1, ndata-1
		wa=X(i); wb=X(i+1)
		wc=Y(i); wd=Y(i+1)
    if (wa.ne.wb) then
      wg = (wd-wc)/(wb-wa)
      wh = om*(wa-xi); wi=om*(wb-xi)
      if (n==0) then
        a = a + (wb-wa)*(wc+wg/2.d0*(wb-wa))
      else 
        wl = cos(wh); wm = sin(wh)
        wn = cos(wi); wp = sin(wi)
        a = a + wg/om*(wn-wl) + wd*wp - wc*wm
        b = b + wg/om*(wp-wm) - wd*wn + wc*wl
      end if
    end if
  end do
  a = a/T; b = b/T
  if (n.ne.0) then
    a = a*2.d0/om; b = b*2.d0/om
  end if
  return
End

  !*******************************************************
  !* Integral of a function FUNC(X) by Romberg's method  *
  !* --------------------------------------------------- *
  !* INPUTS:                                             *
  !*          a      begin value of x variable           *
  !*          b      end value of x variable             *
  !*       prec      desired precision                   *
  !*    itermin      minimum number of iterations        *
  !*    itermax      maximum number of iterations        *
  !*                                                     *
  !* OUTPUTS:                                            *
  !*    obtprec      obtained precision for integral     *
  !*      niter      number of iterations done           *
  !*   integral      the integral of FUNC(X) from a to b *
  !*                                                     *
  !*******************************************************
real*8 Function RombergIntegral(a,b,om,flag,prec,obtprec,niter,itermin,itermax)
    parameter(MAXITER = 15)
	integer flag
    real*8 a,b,om,prec,obtprec,FUNC
    real*8 t(MAXITER,MAXITER)
    real*8 pas,r,s,ta
    if (itermax>MAXITER)  itermax=MAXITER
    r = FUNC(om,a,flag)
    ta = (r + FUNC(om,b,flag)) / 2.d0
    niter=0
    pas=b-a
    t(0,0)=ta*pas
100 niter=niter+1
    pas=pas/2.d0
    s=ta
    do i=1, 2**niter-1
      s = s + FUNC(om,a+pas*i,flag)
    end do
    t(0,niter)=s*pas
    r=1.d0
    do i=1, niter
      r=r*4.d0
      j=niter-i
      t(i,j)=(r*t(i-1,j+1) - t(i-1,j))/(r-1.d0)
    end do
    obtprec = DABS(t(niter,0) - t(niter-1,0))
    if (niter > itermax)  goto 200
    if (niter<itermin)  goto 100
    if (obtprec>prec)   goto 100
200 RombergIntegral = t(niter,0)
    return
end

!****************************************************************
!* Calculate the Fourier harmonic #n of a periodic function F(x)*
!* analytically defined.                                        *
!* ------------------------------------------------------------ *
!* Inputs:                                                      *
!*            t1   : -period/2                                  *
!*            t2   : period/2                                   *
!*            n    : order of harmonic                          *          
!*                                                              *
!* Outputs:                                                     *
!*            a    : coefficient an of the Fourier series.      *
!*            b:   : coefficient bn of the Fourier series.      *
!* ------------------------------------------------------------ *
!* Reference: "Mathematiques en Turbo-Pascal By Marc Ducamp and *
!*             Alain Reverchon, 1. Analyse, Editions Eyrolles,  *
!*             Paris, 1991" [BIBLI 03].                         *
!*                                                              *
!*                           F90 Version By J-P Moreau, Paris.  *
!*                                   (www.jpmoreau.fr)          *
!****************************************************************
! Note:  When a periodic function f(x), of period T, can be developped
!        in a Fourier series, this one is unique:
!                    n=inf.
!        F(x) = a0 + Sum ( an cos(2 n pi/T x) + bn sin(2 n pi/T x)  
!                    n=1
!        (b0 is always zero).!
!
!        The coefficients an, bn are given by:
!                     T/2
!             a0 = 1/T Sum (f(x) dx)
!                      -T/2
!                      T/2
!             an = 2/T Sum (f(x) cos(2npi/T x) dx)
!                      -T/2
!                      T/2
!             an = 2/T Sum (f(x) sin(2npi/T x) dx)
!                      -T/2
!         Here, the integrals are calculated by the Romberg method.
!  --------------------------------------------------------------------
Subroutine AnalyticFourierHn(t1,t2,n,a,b)
real*8 t1,t2,a,b,om
real*8 T,precision,temp, PI
integer flag
  PI=4.d0*datan(1.d0)
  T=dabs(t2-t1)
  om=2.d0*PI*n/T
  precision=1.d-10; itmax=15
  flag=0  ! calculate an
  a=RombergIntegral(t1,t2,om,flag,precision,temp,niter,5,itmax)*2.d0/T
  flag=1  ! calculate bn
  b=RombergIntegral(t1,t2,om,flag,precision,temp,niter,5,itmax)*2.d0/T
  if (n==0)  a=a/2.d0
  return
End

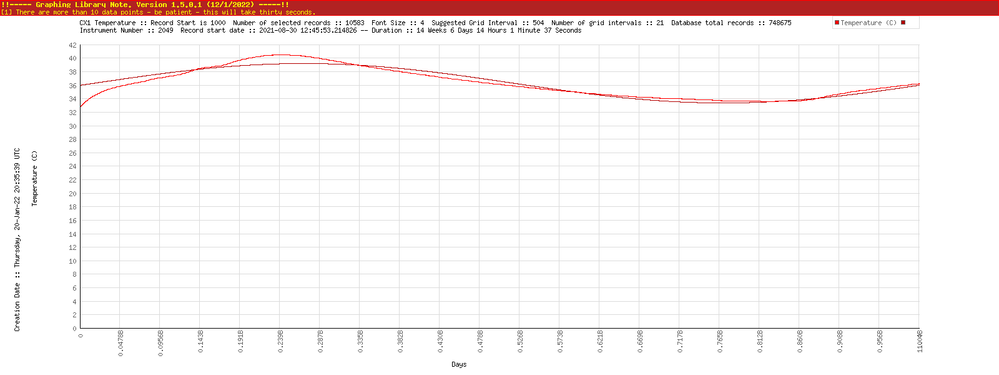
! end of file fourier.f90

part of a set of functions. I have some data in a mySQL database in the cloud and I was wanting to do a Fourier function for the temperature, for some statistical analysis.

So it has been an interesting challenge to translate the Fortran into PHP. PHP is not great with errors, so you go one line at a time, Dreamweaver is not great with formatting automatically , so the do and if statements over a long set of code can become misaligned.

Anyway I got the code running in PHP but matching the input data

JohnNichols · ‎01-20-2022

was proving to be challenging, PHP is not nice to debug with the long cycle times and the lack of nice error output, one ends up using a lot of log files.

So to check the code I created a SLN file for the Fortran and used the same data from the php. The sln file is enclosed.

The final PHP output

and the Fortran output are the same - as expected,

But the Fourier equation has an inversion in the summation, I need to use - instead of +.

 do j = 1,i
    
    z(j) = a(1) - ((a(2)*cos((2.0*3.142/float(i-1))*j)) + (b(2)*sin((2.0*3.142/float(i-1))*j)))
    
    write(14,200)j,x(j),y(j),z(j)
200 Format(i5,3(" , ",f10.3))

The same is true for the PHP.

I will now sit down with my numerical analysis textbook and work out what the problem is in the code, but the French code has the same error in all languages.

Any way it is interesting.

jimdempseyatthecove · ‎01-21-2022

In the comments for subroutine DiscreetFourierHn it lists a and b are outputs, however the code performs summations into a and b with a and b on rhs. IOW the code assumes a and b are used as inputs as well. Either the comment is wrong or the caller must initialize (?0.0, n.m?) these values prior to call.

Jim Dempsey

JohnNichols · ‎01-21-2022

a and b are initialized to zero in the original Fortran code and the PHP code before the summation starts.

The original book is from 1991 and is French, I will have to see if I can find it.

The Numerical Ideas for using this technique appear in the late 1950s, the best one is in the Acoustical Journal, but I need to go to the library to find it. You find the odd reference to the method, but usually it is PPT notes for a lecture where the Professor is demonstrating their math skills and ability to make a ham and cheese sandwich into some French dish.

I have started to back determine the algorithm from the code.

The first step is to transform the 1 -> N from -pi/2 to pi/2.

The next step is to determine the slope on the graph from i to i+ 1 using the standard Newtonian Formula,

I am looking at rewriting the a and b summations with standard symbols so they make some sense, the w's are hard to follow.

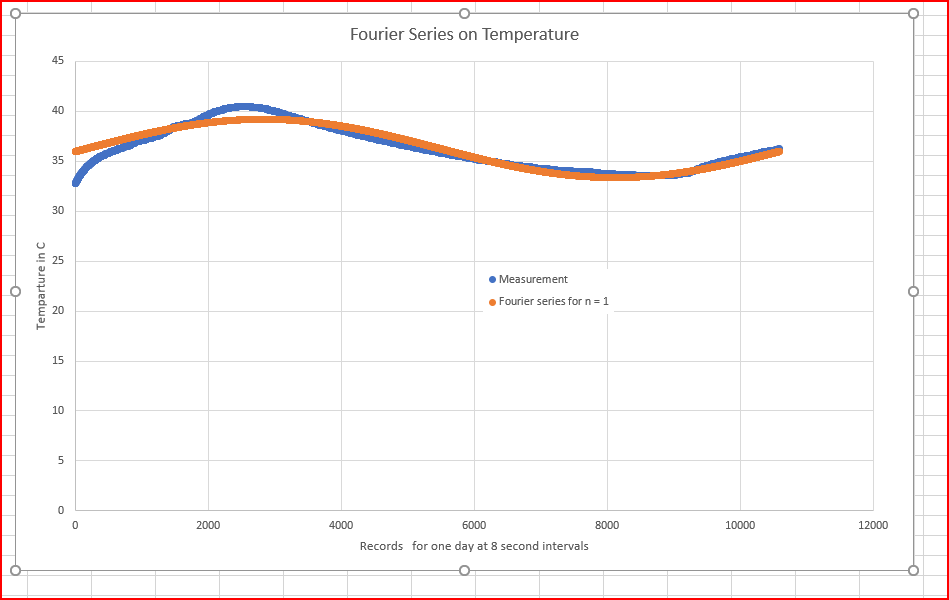
Plus I am only using n = 1 and so as long as the temp is a smooth curve it is ok, longer ones will need higher n's.

JohnNichols · ‎01-21-2022

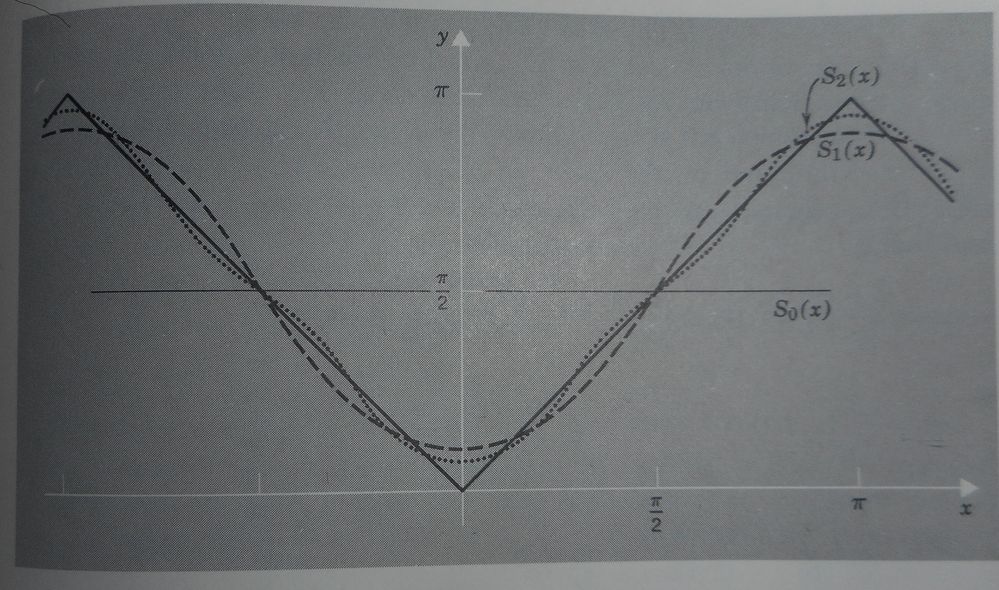
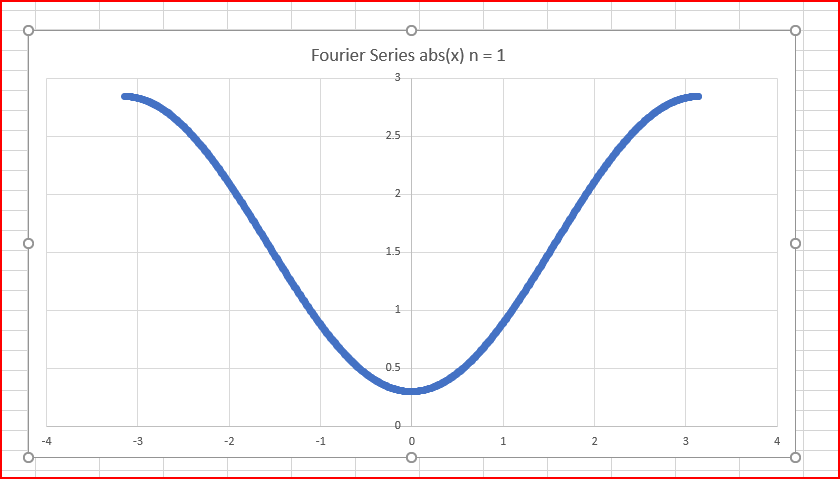
Kaplan and Lewis, Calculus and Linear Algebra - provides a sample calculation for the absolute function from -pi to +p for the Fourier series calculation.

The results from the integration are shown on the picture

The Fourier program predicts the a0, a1, etc to a reasonable number of decimal places, the a(1) value is very close, the first wave is shown

But the final equation still needs the form

z(j) = a(1) - ((a(2)*cos((2.0*3.142/float(i-1))*j)) + (b(2)*sin((2.0*3.142/float(i-1))*j)))

to get the correct answers, otherwise the answers are 1/10th of the real answer.

JohnNichols · ‎01-22-2022

@jimdempseyatthecove , it was my mistake.

z(j) = a(1) + a(2)*cos(x(j)) + b(2)*(sin(x(j)))

I got the Fourier equation wrong, the call is incorrect as you need to use the calculated T in the subroutine in the Fourier equation as he wrote the equation or use the X values directly if they are in Pi format.

JohnNichols · ‎01-22-2022

Well if someone in the future wants a Fourier Series that now works, a copy here is as good as anywhere.