MATMUL

[JohnNichols]

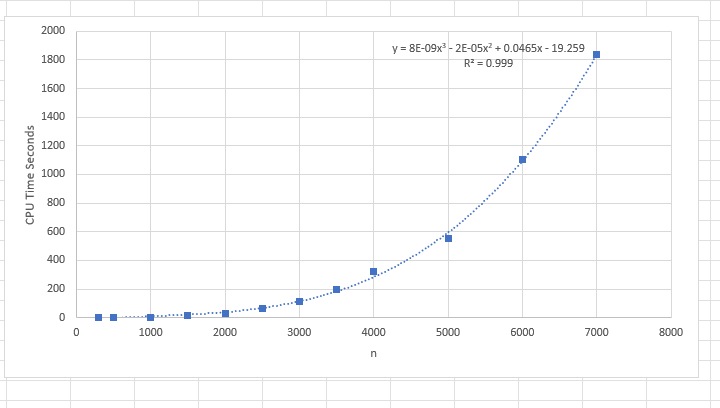
On the Fortran discourse site, there has been a discussion about matmul. The notes include a comparison of the results for different compilers and machines.  

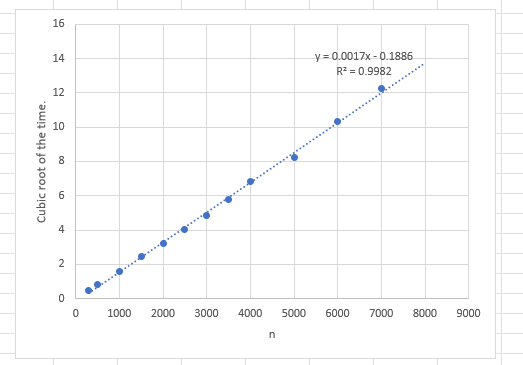
Running the program on IFORT in 32 bit mode, (no idea why 64 bit mode was slower). On a DELL Precision 5570 - Core I7 - 11850H with 32GB memory and a Samsung M2 drive, I get the analysis times shown on the graphs. The first graph is the run time as documented in the program and the second is the cubic root of the run time.  A linear regression shows the time starts to climb above cubic past 6000 by a little bit.  

No other programs running.  

module maprod_mod
    implicit none
    private
    public :: maprod, RP
    integer, parameter :: RP = kind(0.0D0)

    contains

    function maprod(X, Y) result(Z)
    real(RP), intent(in) :: X(:, :), Y(:, :)
    real(RP), allocatable :: Z(:, :)
    integer :: i, j, k

    if (size(X, 2) /= size(Y, 1)) then
        write (*, *) "Wrong size"
        stop
    end if

    allocate (Z(size(X, 1), size(Y, 2)))
    Z = 0.0_RP
    do j = 1, size(Y, 2)
        do i = 1, size(X, 1)
            do k = 1, size(X, 2)
                Z(i, j) = Z(i, j) + X(i, k) * Y(k, j)
            end do
        end do
    end do
    end function maprod

    end module maprod_mod

    program test_matmul
    use, non_intrinsic :: maprod_mod, only : maprod, RP
    implicit none
    integer, parameter :: n = 7000
    real(RP), allocatable :: A(:, :), B(:, :)
    real :: start, finish
    integer i, j, flag

    write (*, *) 'Initialize'
    allocate (A(n, n), B(n, n))
    A = 1.0_RP
    flag = 0

    write (*, *) 'MATMUL'
    call cpu_time(start)
    do i = 1,n
        do j = 1,n
            if(A(I,J) .ne. 0.0_RP) then
                flag = 1
            end if
        end do
    end do
    if(flag == 0) then
        write (*, *) 'Zeros'
    else

        B = matmul(A, A)
    end if
    call cpu_time(finish)
    write (*, *) 'Succeed'
    write (*, *) 'Time in seconds:', finish - start  ! The use of `cpu_time` is questionable. Just ignore it.

    ! Uncomment the following code if you would like to compare `matmul` and `maprod`.
    !call cpu_time(start)
    !B = maprod(A, A)
    !call cpu_time(finish)
    !write (*, *) 'Succeed'
    !write (*, *) 'Time in seconds:', finish - start

    end program test_matmul

 

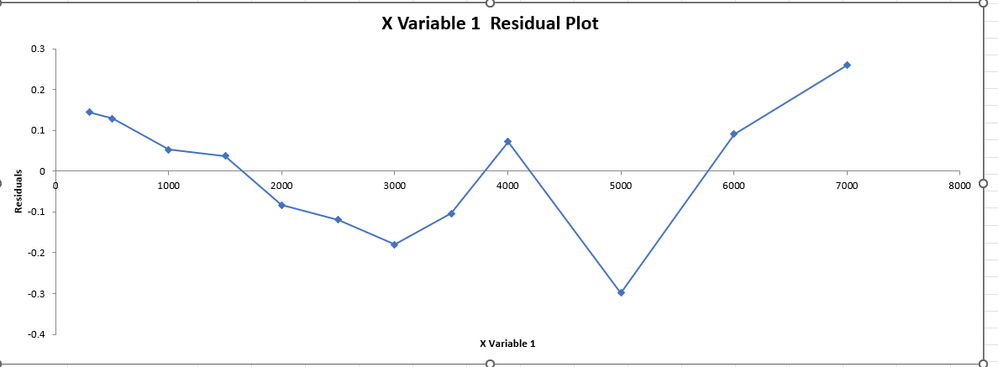
A linear regression on the second chart yields residuals that are interesting. 

An algorithm that is O(n*n*n) is not optimal based on current publications.  

Also if you search for any zero columns or rows, you should be able to reduce the run time.  

Somewhere between 7000 and 10000 you hit a VM limit.  

I changed the program so all the values are 1 and added in a check for all zeros on the matrix, which runs in 0.1 seconds.  

[JohnNichols]

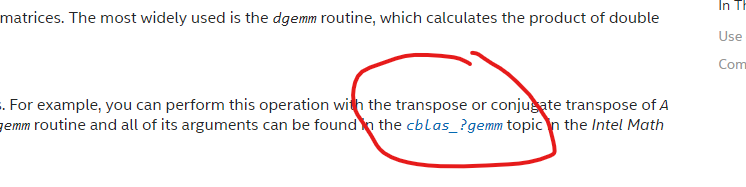
As Dr Fortran has noted, there are broken links on the Intel website.

https://www.intel.com/content/www/us/en/develop/documentation/mkl-tutorial-c/top/multiplying-matrices-using-dgemm.html 

The links point to generic pages, not the actual contents listed, some of those pages have 50 other links, and by the time you scan through you are lost.   The links point to pretty simple things you should not have to then hunt for on your website.  

Sample Picture of broken link - all do not work properly. 

[John_Campbell]

John,

I would be interested if you could provide your statistics using a preferred DO order.

! I do not like the DO order in this example
    do j = 1, size(Y, 2)
        do i = 1, size(X, 1)
            do k = 1, size(X, 2)
                Z(i, j) = Z(i, j) + X(i, k) * Y(k, j)
            end do
        end do
    end do

!  an improvement for memory access is
    do j = 1, size(Y, 2)
        do k = 1, size(X, 2)
            do i = 1, size(X, 1)
                Z(i, j) = Z(i, j) + X(i, k) * Y(k, j)
            end do
        end do
    end do

!  which using array syntax can become 
    do j = 1, size(Y, 2)
        do k = 1, size(X, 2)
            Z(:, j) = Z(:, j) + X(:, k) * Y(k, j)
        end do
    end do

This DO order is also suitable for !$OMP for larger examples

I have now included an adaption to the original post that tests different approaches for DO order, partitioning and OpenMP to improve L1 and L3 cache usage and SIMD instructions. These are only partly successful, so a start to identify some problems that remain.

Perhaps others can identify better approaches for improving efficiency for larger memory problems.

It is important to differentiate the cache inefficiency, that occurrs with larger n, from the O(n^3) op count.

[John_Campbell]

An enhanced version with extra OpenMP test.

[JohnNichols]

Sorry a bit busy.