RSA Numbers

JohnNichols · ‎12-30-2021

I am a bit lost.

The RSA standard defines a block - I assume it can hold numbers as shown on

https://en.wikipedia.org/wiki/ASN.1

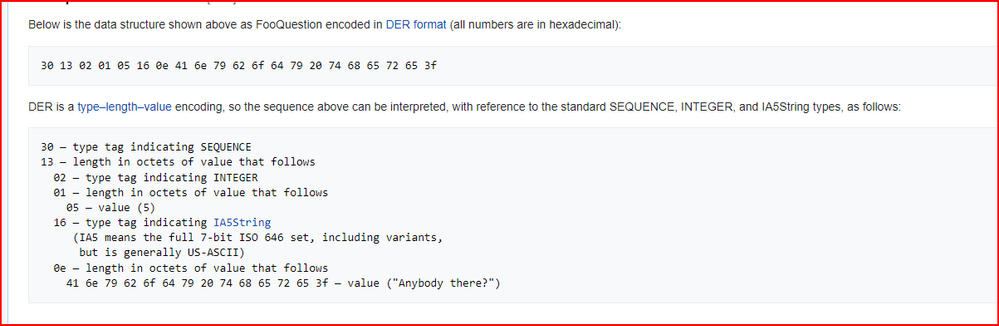
A picture of the format is shown below:

I am trying to work out what is the largest integer available in this format string?

I think I am looking at a 14 digit number? But I am not sure?

Anyone ever worked with this format?

JohnNichols · ‎12-30-2021

subroutine patternR(j, m, prime, cij, h, counter)

    implicit none
    integer(kind=selected_int_kind(15)):: m
    integer(kind=selected_int_kind(15)):: prime
    integer(kind=selected_int_kind(15)):: i
    ! integer(kind=selected_int_kind(15)):: coeff(nprimemax)
    integer(kind=selected_int_kind(15)):: num
    integer(kind=selected_int_kind(15)):: k
    integer(kind=selected_int_kind(15)):: j
    integer(kind=selected_int_kind(15)):: cij
    integer(kind=selected_int_kind(15)):: h
    integer(kind=selected_int_kind(15)):: cjTemp

    counter = 1

This code did not throw an error in VS 2022 that counter was not defined. It ran several times before I noticed the error.

Arjen_Markus · ‎12-31-2021

What integer do you mean? If I understand the ASN.1 or better DER format correctly (referring to the WIkipedia page), then the last part is a string of 14 characters, encoded as 7-bits ASCII, not a decimal or hexadecimal representation of an integer.

But perhaps a better question is: could you explain what you want to do? That may help us understand your questions about details such as the above.

JohnNichols · ‎12-31-2021

The design of RSA encryption relies on the development of a very large composite number with the property that it is a product of just two primes. The algorithm also includes a number of "safeguards" that are supposed to improve the safety of the number system.

The key has to provide two numbers N - the large composite and the e value.

I was looking to how the RSA standard packs the N and the e value into the public key. The RSA documents are interestingly terse.

Late last night I found a PHP implementation of the RSA algorithm, as I program in PHP, one needs to for web site development, I can take the code apart and find the implementation method.

I want to be able to read the RSA number into Fortran and to get some sample numbers.

There is a VSIX package for PHP, so hopefully I can run the PHP code.

Thanks for the reply.

JohnNichols · ‎12-31-2021

* Math_BigInteger uses base-2**26 to perform operations such as multiplication and division and
 * base-2**52 (ie. two base 2**26 digits) to perform addition and subtraction.  Because the largest possible
 * value when multiplying two base-2**26 numbers together is a base-2**52 number, double precision floating
 * point numbers - numbers that should be supported on most hardware and whose significand is 53 bits - are
 * used.  As a consequence, bitwise operators such as >> and << cannot be used, nor can the modulo operator %,
 * which only supports integers.  Although this fact will slow this library down, the fact that such a high
 * base is being used should more than compensate.

This is from the RSA PHP package, the limitations are the things you need to know. These implementation limitations are interesting.

A two raised to the 52 power is only a 15 digit decimal, well within Fortran limits.

I am just playing at xmas and New years while my daughter sleeps in.

JohnNichols · ‎12-31-2021

Found 40549097219 primes up to 200000000000 in 321088. milliseconds. From IFORT

Found 8046173780 primes up to 200000000000 in 220502. milliseconds.

FROM IFX

For this program :: from Rosetta Stone - Sieve of Ert... - the only difference is the selection of the compiler.

The IFORT answer matches another sieve program and they form a straight plot on a log scale, until I use IFX?

subroutine cullSieveBuffer(lwi, size, bpa, sba)
 
    implicit none
    integer(kind=selected_int_kind(15)), intent(in) :: lwi, size
    byte, intent(in) :: bpa(0:size - 1)
    byte, intent(out) :: sba(0:size - 1)
    integer(kind=selected_int_kind(15)) :: i_limit, i_bitlmt, i_bplmt, i, sqri, bp, si, olmt, msk, j
    byte, dimension (0:7) :: bits
    common /twiddling/ bits
 
    i_bitlmt = size * 8 - 1
    i_limit = lwi + i_bitlmt
    i_bplmt = size / 4
    sba = 0
    i = 0
    sqri = (i + i) * (i + 3) + 3
    do while (sqri <= i_limit)
      if (iand(int(bpa(shiftr(i, 3))), shiftl(1, iand(i, 7))) == 0) then
        ! start index address calculation...
        bp = i + i + 3
        if (lwi <= sqri) then
          si = sqri - lwi
        else
          si = mod((lwi - sqri), bp)
          if (si /= 0) si = bp - si
        end if
        if (bp <= i_bplmt) then
          olmt = min(i_bitlmt, si + bp * 8 - 1)
          do while (si <= olmt)
            msk = bits(iand(si, 7))
            do j = shiftr(si, 3), size - 1, bp
              sba(j) = ior(int(sba(j)), msk)
            end do
            si = si + bp
          end do
        else
          do while (si <= i_bitlmt)
            j = shiftr(si, 3)
            sba(j) = ior(sba(j), bits(iand(si, 7)))
            si = si + bp
          end do
        end if
      end if
      i = i + 1
      sqri = (i + i) * (i + 3) + 3
    end do
 
  end subroutine cullSieveBuffer
 
  integer(kind=selected_int_kind(15)) function countSieveBuffer(lmti, almti, sba)
 
    implicit none
    integer(kind=selected_int_kind(15)), intent(in) :: lmti, almti
    byte, intent(in) :: sba(0:almti)
    integer(kind=selected_int_kind(15)) :: bmsk, lsti, i, cnt
    byte, dimension (0:65535) :: clut
    common /counting/ clut
 
    cnt = 0
    bmsk = iand(shiftl(-2, iand(lmti, 15)), 65535)
    lsti = iand(shiftr(lmti, 3), -2)
    do i = 0, lsti - 1, 2
      cnt = cnt + clut(shiftl(iand(int(sba(i)), 255),  + iand(int(sba(i + 1)), 255))
    end do
    countSieveBuffer = cnt + clut(ior(shiftl(iand(int(sba(lsti)), 255),  + iand(int(sba(lsti + 1)), 255), bmsk))
 
  end function countSieveBuffer
 
  program sieve_paged
 
    use OMP_LIB
    implicit none
    integer(kind=selected_int_kind(15)), parameter :: i_max = 200000000000, i_range = (i_max - 3) / 2
    integer(kind=selected_int_kind(15)), parameter :: i_l1cache_size = 16384, i_l1cache_bitsz = i_l1cache_size * 8
    integer(kind=selected_int_kind(15)), parameter :: i_l2cache_size = i_l1cache_size * 8, i_l2cache_bitsz = i_l2cache_size * 8
    integer(kind=selected_int_kind(15)) :: cr, c0, c1, i, j, k, cnt
    integer(kind=selected_int_kind(15)), save :: scnt
    integer(kind=selected_int_kind(15)) :: countSieveBuffer
    integer(kind=selected_int_kind(15)) :: numthrds
    byte, dimension (0:i_l1cache_size - 1) :: bpa
    byte, save, allocatable, dimension (:) :: sba
    byte, dimension (0:7) :: bits = (/ 1, 2, 4, 8, 16, 32, 64, -128 /)
    byte, dimension (0:65535) :: clut
    common /twiddling/ bits
    common /counting/ clut
 
    type heaparr
      byte, allocatable, dimension(:) :: thrdsba
    end type heaparr
    type(heaparr), allocatable, dimension (:) :: sbaa
 
    !$OMP THREADPRIVATE(scnt, sba)
 
    numthrds = 1
    !$ numthrds = OMP_get_max_threads()
    allocate(sbaa(0:numthrds - 1))
    do i = 0, numthrds - 1
      allocate(sbaa(i)%thrdsba(0:i_l2cache_size - 1))
    end do
 
    CALL SYSTEM_CLOCK(count_rate=cr)
    CALL SYSTEM_CLOCK(c0)
    do k = 0, 65535 ! initialize counting Look Up Table
      j = k
      i = 16
      do while (j > 0)
        i = i - 1
        j = iand(j, j - 1)
      end do
      clut(k) = i
    end do
    bpa = 0 ! pre-initialization not guaranteed!
    call cullSieveBuffer(0, i_l1cache_size, bpa, bpa)
    cnt = 1
    !$OMP PARALLEL DO ORDERED
      do i = i_l2cache_bitsz, i_range, i_l2cache_bitsz * 8
        scnt = 0
        sba = sbaa(mod(i, numthrds))%thrdsba
        do j = i, min(i_range, i + 8 * i_l2cache_bitsz - 1), i_l2cache_bitsz
          call cullSieveBuffer(j - i_l2cache_bitsz, i_l2cache_size, bpa, sba)
          scnt = scnt + countSieveBuffer(i_l2cache_bitsz - 1, i_l2cache_size, sba)
        end do
        !$OMP ATOMIC
          cnt = cnt + scnt
          
    write(*,100)
100 Format("."\)    
      end do
    !$OMP END PARALLEL DO
 
    j = i_range / i_l2cache_bitsz * i_l2cache_bitsz
    k = i_range - j
    if (k /= i_l2cache_bitsz - 1) then
      call cullSieveBuffer(j, i_l2cache_size, bpa, sbaa(0)%thrdsba)
      cnt = cnt + countSieveBuffer(k, i_l2cache_size, sbaa(0)%thrdsba)
    end if
  !  write (*, '(i0, 1x)', advance = 'no') 2
  !  do i = 0, i_range
  !    if (iand(sba(shiftr(i, 3)), bits(iand(i, 7))) == 0) write (*, '(i0, 1x)', advance='no') (i + i + 3)
  !  end do
  !  write (*, *)
    CALL SYSTEM_CLOCK(c1)
    print '(a, i0, a, i0, a, f0.0, a)', 'Found ', cnt, ' primes up to ', i_max, &
          ' in ', ((c1 - c0) / real(cr) * 1000), ' milliseconds.'
 
    do i = 0, numthrds - 1
      deallocate(sbaa(i)%thrdsba)
    end do
    deallocate(sbaa)
 
  end program sieve_paged

jimdempseyatthecove · ‎12-31-2021

Your parallel do (DO I) contains an inner loop DO J, J should be made PRIVATE on the !$OMP PARALLEL directive.

See what happens when making this change.

Jim Dempsey

JohnNichols · ‎12-31-2021

I added the following private. I tested and it worked perfectly until the number i_max reaches

2000000000000

then the answers diverges downward by several hundredfold.

program sieve_paged
 
    use OMP_LIB
    implicit none
    integer(kind=selected_int_kind(15)), parameter :: i_max = 2000000000000, i_range = (i_max - 3) / 2
    integer(kind=selected_int_kind(15)), parameter :: i_l1cache_size = 16384, i_l1cache_bitsz = i_l1cache_size * 8
    integer(kind=selected_int_kind(15)), parameter :: i_l2cache_size = i_l1cache_size * 8, i_l2cache_bitsz = i_l2cache_size * 8
    integer(kind=selected_int_kind(15)) :: cr, c0, c1, i, j, k, cnt
    integer(kind=selected_int_kind(15)), save :: scnt
    integer(kind=selected_int_kind(15)) :: countSieveBuffer
    integer(kind=selected_int_kind(15)) :: numthrds
    byte, dimension (0:i_l1cache_size - 1) :: bpa
    byte, save, allocatable, dimension (:) :: sba
    byte, dimension (0:7) :: bits = (/ 1, 2, 4, 8, 16, 32, 64, -128 /)
    byte, dimension (0:65535) :: clut
    common /twiddling/ bits
    common /counting/ clut
 
    type heaparr
      byte, allocatable, dimension(:) :: thrdsba
    end type heaparr
    type(heaparr), allocatable, dimension (:) :: sbaa
 
    !$OMP THREADPRIVATE(scnt, sba)
 
    numthrds = 1
    !$ numthrds = OMP_get_max_threads()
    allocate(sbaa(0:numthrds - 1))
    do i = 0, numthrds - 1
      allocate(sbaa(i)%thrdsba(0:i_l2cache_size - 1))
    end do
 
    CALL SYSTEM_CLOCK(count_rate=cr)
    CALL SYSTEM_CLOCK(c0)
    do k = 0, 65535 ! initialize counting Look Up Table
      j = k
      i = 16
      do while (j > 0)
        i = i - 1
        j = iand(j, j - 1)
      end do
      clut(k) = i
    end do
    bpa = 0 ! pre-initialization not guaranteed!
    call cullSieveBuffer(0, i_l1cache_size, bpa, bpa)
    cnt = 1
    !$OMP PARALLEL DO ORDERED PRIVATE(J)
      do i = i_l2cache_bitsz, i_range, i_l2cache_bitsz * 8
        scnt = 0
        sba = sbaa(mod(i, numthrds))%thrdsba
        do j = i, min(i_range, i + 8 * i_l2cache_bitsz - 1), i_l2cache_bitsz
          call cullSieveBuffer(j - i_l2cache_bitsz, i_l2cache_size, bpa, sba)
          scnt = scnt + countSieveBuffer(i_l2cache_bitsz - 1, i_l2cache_size, sba)
        end do
        !$OMP ATOMIC
          cnt = cnt + scnt
          
    write(*,100)
100 Format("."\)    
      end do
    !$OMP END PARALLEL DO

jimdempseyatthecove · ‎01-01-2022

Without debugging this on your system I can only guess.

Try running this with bounds checking enabled (it is going to take quite a while). Maybe something will show up.

It is hard to imagine that if the code works with i_max=2,000,000,000,000 that it would fail with i_max=4,000,000,000,000.

Both values are well within the range of an integer(8) 9,223,372,036,854,775,807

Jim Dempsey

JohnNichols · ‎01-01-2022

I partially found the problem, the method is built on binary analysis, the array sizes that are binary are related to the maximum integer number, but the designed was ok as along as imax is low, as it gets higher you need to increase a number of the array sizes, as shown

    subroutine cullSieveBuffer(lwi, size, bpa, sba)

    implicit none
    integer(kind=selected_int_kind(15)), intent(in) :: lwi, size
    integer(kind=selected_int_kind(15)) ASD
    byte, intent(in) :: bpa(0:size - 1)
    byte, intent(out) :: sba(0:size - 1)
    integer :: i_limit, i_bitlmt, i_bplmt, i, sqri, bp, si, olmt, msk, j
    byte, dimension (0:7) :: bits
    common /twiddling/ bits

    i_bitlmt = size * 8 - 1
    i_limit = lwi + i_bitlmt
    i_bplmt = size / 4
    sba = 0
    i = 0
    sqri = (i + i) * (i + 3) + 3
    do while (sqri <= i_limit)
        if(mod(i,10000000) == 0) then
        ASD = shiftr(i, 3)
            write(*,*)"Count value :: ",i," Shift value :: ", ASD
        end if
        ASD = int(bpa(shiftr(i, 3)))
        if (iand(ASD, shiftl(1, iand(i, 7))) == 0) then
            ! start index address calculation...
            bp = i + i + 3
            if (lwi <= sqri) then
                si = sqri - lwi
            else
                si = mod((lwi - sqri), bp)
                if (si /= 0) si = bp - si
            end if
            if (bp <= i_bplmt) then
                olmt = min(i_bitlmt, si + bp * 8 - 1)
                do while (si <= olmt)
                    msk = bits(iand(si, 7))
                    do j = shiftr(si, 3), size - 1, bp
                        sba(j) = ior(int(sba(j)), msk)
                    end do
                    si = si + bp
                end do
            else
                do while (si <= i_bitlmt)
                    j = shiftr(si, 3)
                    sba(j) = ior(sba(j), bits(iand(si, 7)))
                    si = si + bp
                end do
            end if
        end if
        i = i + 1
        sqri = (i + i) * (i + 3) + 3
    end do

    end subroutine cullSieveBuffer

    integer(kind=selected_int_kind(15)) function countSieveBuffer(lmti, almti, sba)

    implicit none
    integer(kind=selected_int_kind(15)),intent(in) :: lmti, almti
    byte, intent(in) :: sba(0:almti)
    integer :: bmsk, lsti, i, cnt
    byte, dimension (0:65535) :: clut
    common /counting/ clut

    cnt = 0
    bmsk = iand(shiftl(-2, iand(lmti, 15)), 65535)
    lsti = iand(shiftr(lmti, 3), -2)
    do i = 0, lsti - 1, 2
        cnt = cnt + clut(shiftl(iand(int(sba(i)), 255),  + iand(int(sba(i + 1)), 255))
    end do
    countSieveBuffer = cnt + clut(ior(shiftl(iand(int(sba(lsti)), 255),  + iand(int(sba(lsti + 1)), 255), bmsk))

    end function countSieveBuffer

    !--------------------------------------------------------------------------------------------------------------------------

    program sieve_paged

    use OMP_LIB
    implicit none
    integer(kind=selected_int_kind(15)), parameter :: nn = 17
    integer(kind=selected_int_kind(15)), parameter :: ii = 2**nn
    integer(kind=selected_int_kind(15)), parameter :: nm = ii * 16 - 1
    integer(kind=selected_int_kind(15)), parameter :: mm = ii*9182
    integer(kind=selected_int_kind(15)), parameter :: i_max = mm, i_range = (i_max - 3) / 2
    integer(kind=selected_int_kind(15)), parameter :: i_l1cache_size = ii * 8 , i_l1cache_bitsz = i_l1cache_size * 8
    integer(kind=selected_int_kind(15)), parameter :: i_l2cache_size = i_l1cache_size * 8, i_l2cache_bitsz = i_l2cache_size * 8
    integer(kind=selected_int_kind(15)) :: cr, c0, c1, i, j, k, cnt
    integer(kind=selected_int_kind(15)), save :: scnt
    integer(kind=selected_int_kind(15)):: countSieveBuffer
    integer(kind=selected_int_kind(15)) :: numthrds
    byte, dimension (0:i_l1cache_size - 1) :: bpa
    byte, save, allocatable, dimension (:) :: sba
    byte, dimension (0:7) :: bits = (/ 1, 2, 4, 8, 16, 32, 64, -128 /)
    byte, dimension (0:nm) :: clut
    common /twiddling/ bits
    common /counting/ clut

    type heaparr
        byte, allocatable, dimension(:) :: thrdsba
    end type heaparr
    type(heaparr), allocatable, dimension (:) :: sbaa
    
    open(33,file ="data.txt", status = "unknown")

    !$OMP THREADPRIVATE(scnt, sba)

    numthrds = 1
    !$ numthrds = OMP_get_max_threads()
    
    allocate(sbaa(0:numthrds - 1))
    do i = 0, numthrds - 1
        allocate(sbaa(i)%thrdsba(0:i_l2cache_size - 1))
    end do

    CALL SYSTEM_CLOCK(count_rate=cr)
    CALL SYSTEM_CLOCK(c0)
    do k = 0, nm ! initialize counting Look Up Table
        j = k
        i = 16
        do while (j > 0)
            i = i - 1
            j = iand(j, j - 1)
        end do
        clut(k) = i
    end do
    bpa = 0 ! pre-initialization not guaranteed!
    call cullSieveBuffer(0, i_l1cache_size, bpa, bpa)

    cnt = 1
    !$OMP PARALLEL DO ORDERED PRIVATE(J)
    do i = i_l2cache_bitsz, i_range, i_l2cache_bitsz * 8
        scnt = 0
        sba = sbaa(mod(i, numthrds))%thrdsba
        do j = i, min(i_range, i + 8 * i_l2cache_bitsz - 1), i_l2cache_bitsz
            call cullSieveBuffer(j - i_l2cache_bitsz, i_l2cache_size, bpa, sba)
            scnt = scnt + countSieveBuffer(i_l2cache_bitsz - 1, i_l2cache_size, sba)
        end do
        !$OMP ATOMIC
        cnt = cnt + scnt
    end do
    !$OMP END PARALLEL DO

    j = i_range / i_l2cache_bitsz * i_l2cache_bitsz
    k = i_range - j
    if (k /= i_l2cache_bitsz - 1) then
        call cullSieveBuffer(j, i_l2cache_size, bpa, sbaa(0)%thrdsba)
        cnt = cnt + countSieveBuffer(k, i_l2cache_size, sbaa(0)%thrdsba)
    end if
    !  write (*, '(i0, 1x)', advance = 'no') 2
      do i = 0, i_range
        if (iand(sba(shiftr(i, 3)), bits(iand(i, 7))) == 0) write (33,1000) i,(i + i + 3)
1000   Format(i10,3x, i10)        
      end do
      write (*, *)
    CALL SYSTEM_CLOCK(c1)
    print '(a, i0, a, i0, a, f0.0, a)', 'Found ', cnt, ' primes up to ', i_max, &
        ' in ', ((c1 - c0) / real(cr) * 1000), ' milliseconds.'

    do i = 0, numthrds - 1
        deallocate(sbaa(i)%thrdsba)
    end do
    deallocate(sbaa)

    end program sieve_paged

on line 81etc...

But the problem is when you try and get the primes to print, one wants the numbers not just the number of primes less than one million, line 152 crashes long before you reach the end of the list and it does not give you the correct primes. In the Rosetta code site these lines are commented out and obviously the author knows they are wrong and just has never fixed it. It misses, 2, 3, .. 47 and a lot after that.

Line 81, nn = 19 runs out of space in the memory model. All you need is an array that is one bit per element = either 0 or 1. Anything bigger is a complete waste of space. If I take a 4 bit array then you can use the repeat patterns in primes to generate a list. Primes have a small apparent randomness but it is illusionary, they are stable as heck from a set of sawtooth functions.

Fanch29 · ‎01-01-2023

Hello John,

I know that is not a recent post

I'm working (for fun) on a fast prime generator

My purpose is to compare IFORT 2023 vs IFX 2023 vs Gfortran 12

Found the Fortran rosetta source code and then this thread with your improvements

I tried them all

Anyhow I'm not able to get the prime number to be printed

I'm talking about these lines

! write (*, '(i0, 1x)', advance = 'no') 2
! do i = 0, i_range
! if (iand(sba(shiftr(i, 3)), bits(iand(i, 7))) == 0) write (*, '(i0, 1x)', advance='no') (i + i + 3)
! end do
! write (*, *)

They lead to a crash on my side (IFORT 2023 + VS2022)

Have you been able to print for example the 100 first prime numbers with your code?

Would you share you most up to date version?

BR

mecej4 · ‎01-03-2023

@Fanch29,

The Rosettacode site contains several Fortran programs for finding primes, with different levels of sophistication. The one that @JohnNichols and you selected is the "Multi-Threaded Page-Segmented Bit-Packed Odds-Only Version". It is based on allocating and maintaining a bit array, but the code has at least one bug, which is the one that you encountered -- the array BPA is referenced when it is not yet allocated. The corrections needed are not obvious.

Here is a different Fortran program that you may find more suited for your purposes. It is short (about 80 lines) and reasonably fast (it finds primes <= 1,000,000,000 in a few seconds). It will print out the primes if you change .false. to .true. on line-3.

program primes ! Indices start at 1 rather than 0, but values match Python code values
implicit none
logical, parameter :: toShow = .false. !change to .true. to print out primes found
integer, parameter :: RESCNT = 8, MODUL = 30
integer, parameter :: RESID(RESCNT) = [7,11,13,17,19,23,29,31]
integer i,j,k,prm_r,r,s,ri,num,expr, modk, limit, maxprms, SqRtN
integer :: kn(RESCNT,RESCNT),rr(RESCNT,RESCNT),pos(MODUL)
integer iprm,resr,PrimeNum,ress,kni,rri,kpm,nprm,nprimes,istep
logical, allocatable :: prms(:)
character(30) :: arg1
!
if(command_argument_count() /= 1)then
   stop 'Usage: primeseg <nmax> to find primes <= nmax'
endif
pos = 0
do i=1,RESCNT
   pos(RESID(i)-1) = i-1
end do
do r = 1, RESCNT
   prm_r = RESID(r)
   do s = 1, RESCNT
      ri = RESID(s)
      expr = prm_r*ri-2
      kn(s,r) = expr/MODUL
      rr(s,r) = mod(expr,MODUL)
   end do
end do
!
! Now the setup is complete, do the sieving
!
call get_command_argument(1,arg1)
read(arg1,*)limit
num = ior(limit-1,1) ! make odd number
k = (num-2)/MODUL
modk = MODUL*k; r = rescnt-1
do while (num < modk+RESID(r+1))
   r = r-1
end do
maxprms = k*RESCNT+r+1
allocate(prms(maxprms))
print *,'Allocated boolean array of size ',maxprms
prms = .true.
SqRtN = int(sqrt(dble(num)))
modk=0; k=0; r=0; nprimes = maxprms+3 ! +3 for [2, 3, 5]
do iprm = 1,maxprms
   r=r+1
   if(r > rescnt)then
      r = 1; k=k+1; modk=modk+MODUL
   endif
   if(.not.prms(iprm))cycle
   resr = resid(r)
   PrimeNum = modk+resr
   if(PrimeNum > SqRtN)exit
   istep = PrimeNum*RESCNT
   do s=1,RESCNT
      kpm = (k*(PrimeNum+resid(s))+kn(s,r))*RESCNT+POS(rr(s,r)+1)
      prms(kpm+1:maxprms:istep) = .false.
   end do
end do
!count/print primes
if(toShow)then
   modk=0; r=-1
   i=3
   write(*,'(A)',advance='no')'   2   3   5'
   do j=1,maxprms
      r = r+1
      if(r==RESCNT)then
         r = 0; modk = modk+MODUL
      endif
      if(.not.prms(j))cycle
      PrimeNum = modk+resid(r+1)
      if(mod(i,20) == 0)print *
      i = i+1
      write(*,'(1x,i3)',advance='no')PrimeNum
   end do
   nprimes = i
else
   nprimes = count(prms(1:maxprms))+3
endif
print '(/,i12,2x,A)',nprimes,'primes found'
end program

Fanch29 · ‎01-04-2023

@mecej4

Thank you very much for your answer

I was not sure anyone would ...

I did rework a little your code to reach 10^10 so I can compare with other codes I have already tried.

This one is counting the PN up to 10^10 in 28sec (but not yet storing the result in an array - need some more work/time)

My 2 previous attempts did 34sec (based on Matlab code) or 32 sec (Based on Rcpp code)

Fortran being a bit faster than Matlab or R ... but not that much

So yes this code a bit faster ... the "rosetta " code is doing that in 6sec... I'm a bit reluctant to give up

For the purpose of comparing the compilers, these codes will do the job

For the purpose of creating a function (a DLL) ... a fast one ... I would rather keep the Rosetta version

I'll keep you updated

jimdempseyatthecove · ‎01-02-2022

Found a problem with your code:

...
byte, save, allocatable, dimension(:) :: sba
...
!$OMP THREADPRIVATE(scnt, sbp)
...
!$OMP PARALLEL DO ORDERED PRIVATE(J)
...
   sba = sbaa(mod(i, numthrds))%thrdsba
...
!$OMP END PARALLEL DO
...
if(iand(sba(shiftr(i, 3) ...

While line 8 defines a threadprivate sba (for the specific threads executing that statement), the line 12 sba reference is that of only the main thread and not a compendium of all thread(s) thrdsba's

Further, the statement on line 8 sets the size of sba to i_l2cache_size and not that of i_range.

Next the parallel do loop's call cullSieveBuffer sets threadprivate sba, but then after the call you do not return the set value back into the thread's thrdsba.

Also, why doesn't the parallel do start at i=0?

These are likely an incomplete set of inconsistencies.

Jim Dempsey

JohnNichols · ‎01-02-2022

@jimdempseyatthecove , thank you for your help. This program is full of interesting problems, and it has the severe limitation that no matter how many we fix, it is limited to the 2 GB.

The simplest way to overcome this problem is to write a new sieve program that leaves the data in files and only loads them into memory as needed. I spent several fruitful hours yesterday and wrote that program.

It is a bit slow, but it does not stop - well on my tests so far, it gets all the numbers correct - I do not think I can parallelize it easily, although you could thread it - give each thread a lump say a million etc...

If you cannot climb the mountain one way - find another path.

Here is the code:

    program main

    implicit none

    integer(kind=selected_int_kind(15)), parameter :: number = 9
    integer(kind=selected_int_kind(15)) :: num, i, flag, numb, ind, prime, limit
    real(8) j
    integer file1
    integer file2
    integer file3
    integer file4
    integer swap
    integer IENQ
    integer nums(100)
    integer(kind=selected_int_kind(15)) :: cr, c0, c1, k
    integer cnt

    CALL SYSTEM_CLOCK(count_rate=cr)
    CALL SYSTEM_CLOCK(c0)

    limit = 1000000
    flag = 0
    file1 = 33
    file2 = 34
    file3 = 35
    file4 = 36
    cnt = 0

    num = huge(num)
    swap = 1
    nums = 0
    open(file1,file = "huge.out", status = "unknown")
    open(file2,file = "huge1.out", status = "unknown")
    open(file3,file = "primes.out", status = "unknown")
    open(file4,file = "primes.csv", status = "unknown")

    write(*,*)num
    write(file3,10)2,1
    nums(2) = nums(2) + 1
    nums(3) = nums(3) + 1
    cnt = cnt + 2
    write(file3,10)3,1
10  format(i2,1x,i1)

    call loadnumbers(num, limit, file1)
    rewind(file1)
    do while(flag == 0)

        call findnextprime(prime, file1, file2, file3,flag, cnt, nums)
        if(flag == 0) then
            
                write(*,200)prime
200             format("   Searching for factors of :: ",i10)
        end if

        call loopforprime(prime,file1, file2)

        if(swap == 1) then
            close(file1, STATUS='DELETE', IOSTAT=IENQ)
            close(file2)
            open(file2,file = "huge.out", status = "unknown")
            open(file1,file = "huge1.out", status = "unknown")
            swap = 2
        else if(swap == 2) then
            close(file1, STATUS='DELETE', IOSTAT=IENQ)
            close(file2)
            open(file1,file = "huge.out", status = "unknown")
            open(file2,file = "huge1.out", status = "unknown")
            swap = 1
        end if

    end do

    write(*,204)
204 Format(///,"  last Digits          Count",/)

    do i = 1, 99
        write(*,202)I,nums(i)
        write(file4,203)I,nums(i)
202     Format(5x,I2,10x, i10)
203     Format(I2,",", i10)
    end do
    CALL SYSTEM_CLOCK(c1)
    print '(//,a, i0, a, i0, a, f7.1, a,//)', '   Found ', cnt, ' primes up to ', limit, &
        ' in ', ((c1 - c0) / real(cr) ), ' seconds.'

    close(file3)
    write(*,201)
201 Format(" Finished Analysis. The results are in huge1.out.",//)

    end program

    !-----------------------------------------------------------------------------------------------------------------------------------------------------------------------
    !
    !
    !
    !------------------------------------------------------------------------------------------------------------------------------------------------------------------------

    subroutine loadnumbers(num, limit, file1)

    implicit none

    integer(kind=selected_int_kind(15)) :: i, limit, num
    integer file1
    real(8) j


    do i = 3,limit,2
        if(mod(i,100001) == 0) then
            j = real(i)/real(limit)
            write(*,*)i,j
        end if
        if(mod(i,3) == 0) then
        else
            if(i < 10) then
                write(file1,10)i,0
10              format(i2,1x,i1)
            else if(i < 100) then

                write(file1,100)i,0
100             format(i3,1x,i1)
            else if(i < 1000) then

                write(file1,102)i,0
102             format(i4,1x,i1)
            else if(i < 10000) then

                write(file1,103)i,0
103             format(i5,1x,i1)
            else if(i < 100000) then

                write(file1,104)i,0
104             format(i6,1x,i1)
            else if(i < 1000000) then

                write(file1,105)i,0
105             format(i7,1x,i1)
            else if(i < 10000000) then

                write(file1,106)i,0
106             format(i8,1x,i1)
            else if(i < 100000000) then

                write(file1,107)i,0
107             format(i9,1x,i1)
            else if(i < 1000000000) then

                write(33,108)i,0
108             format(i10,1x,i1)
            else if(i < 1000000000) then

                write(file1,109)i,0
109             format(i11,1x,i1)
            else if(i < 100000000000) then

                write(file1,110)i,0
110             format(i2,1x,i1)
            else if(i < 1000000000000) then

                write(file1,111)i,0
111             format(i3,1x,i1)
            else if(i < 10000000000000) then

                write(file1,112)i,0
112             format(i14,1x,i1)
            else if(i < 100000000000000) then

                write(file1,113)i,0
113             format(i15,1x,i1)

            end if
        end if
    end do

    return
    end subroutine loadnumbers


    !-----------------------------------------------------------------------------------------------------------------------------------------------------------------------
    !
    !
    !
    !------------------------------------------------------------------------------------------------------------------------------------------------------------------------


    subroutine findnextprime(prime, file1,file2, file3, flag1, cnt, nums)

    implicit none

    integer(kind=selected_int_kind(15)), intent(INOUT) :: prime
    integer, intent(In) :: file1,file2, file3
    integer(kind=selected_int_kind(15)), intent(InOUT) :: flag1
    integer(kind=selected_int_kind(15)) :: num, i, flag, numb, ind
    integer, intent(inout) :: cnt, nums(100)
    real set, setL
    set = 0.0
    setL = 0.0
    flag = 0
    do while(flag ==0)
        read(file1,*, err = 200, end = 200)numb,ind
        cnt = cnt + 1
11      format(i2,1x,i1)
        if(ind == 0) then
            prime = numb
            flag = 1
            ind = 1
            set = float(prime)/100.0
            setL = floor(set)
            set = (set-setL) * 100
            ! write(*,*)set
            if( int(set) > 0 .and. int(set) < 100) then
                nums(int(set)) = nums(int(set)) + 1
            end if

        end if
        if(numb < 10) then
            write(file3,10)numb,ind
10          format(i2,1x,i1)
        else if(numb  < 100) then

            write(file3,100)numb,ind
100         format(i3,1x,i1)
        else if(numb  < 1000) then

            write(file3,102)numb,ind
102         format(i4,1x,i1)
        else if(numb  < 10000) then

            write(file3,103)numb,ind
103         format(i5,1x,i1)
        else if(numb  < 100000) then

            write(file3,104)numb,ind
104         format(i6,1x,i1)
        else if(numb  < 1000000) then

            write(file3,105)numb,ind
105         format(i7,1x,i1)
        else if(numb  < 10000000) then

            write(file3,106)numb,ind
106         format(i8,1x,i1)
        else if(numb  < 100000000) then

            write(file3,107)numb,ind
107         format(i9,1x,i1)
        else if(numb  < 1000000000) then

            write(file3,108)numb,ind
108         format(i10,1x,i1)
        else if(numb  < 1000000000) then

            write(file3,109)numb,ind
109         format(i11,1x,i1)
        else if(numb  < 100000000000) then

            write(file3,110)numb,ind
110         format(i2,1x,i1)
        else if(numb  < 1000000000000) then

            write(file3,111)numb,ind
111         format(i3,1x,i1)
        else if(numb  < 10000000000000) then

            write(file3,112)numb,ind
112         format(i14,1x,i1)
        else if(numb  < 100000000000000) then

            write(file3,113)numb,ind
113         format(i15,1x,i1)

        end if

    end do

    return
200 flag1 = 1

    end subroutine findnextprime


    !-----------------------------------------------------------------------------------------------------------------------------------------------------------------------
    !
    !
    !
    !------------------------------------------------------------------------------------------------------------------------------------------------------------------------


    subroutine loopforprime(prime,file1, file2)

    integer(kind=selected_int_kind(15)), intent(INOUT) :: prime
    integer, intent(In) :: file1, file2
    integer(kind=selected_int_kind(15)) :: flag,numb, ind


    flag = 0
    do while(flag == 0)
        read(file1,*, end = 50)numb,ind
        if(mod(numb,prime) == 0) then

        else
            if(numb < 10) then
                write(file2,10)numb,ind
10              format(i2,1x,i1)
            else if(numb < 100) then

                write(file2,100)numb,ind
100             format(i3,1x,i1)
            else if(numb < 1000) then

                write(file2,102)numb,ind
102             format(i4,1x,i1)
            else if(numb < 10000) then

                write(file2,103)numb,ind
103             format(i5,1x,i1)
            else if(numb < 100000) then

                write(file2,104)numb,ind
104             format(i6,1x,i1)
            else if(numb < 1000000) then

                write(file2,105)numb,ind
105             format(i7,1x,i1)
            else if(numb < 10000000) then

                write(file2,106)numb,ind
106             format(i8,1x,i1)
            else if(numb < 100000000) then

                write(file2,107)numb,ind
107             format(i9,1x,i1)
            else if(numb < 1000000000) then

                write(file2,108)numb,ind
108             format(i10,1x,i1)
            else if(numb < 1000000000) then

                write(file2,109)numb,ind
109             format(i11,1x,i1)
            else if(numb < 100000000000) then

                write(file2,110)numb,ind
110             format(i2,1x,i1)
            else if(numb < 1000000000000) then

                write(file2,111)numb,ind
111             format(i3,1x,i1)
            else if(numb < 10000000000000) then

                write(file2,112)numb,ind
112             format(i14,1x,i1)
            else if(numb < 100000000000000) then

                write(file2,113)numb,ind
113             format(i15,1x,i1)

            end if
        end if


    end do

50  return
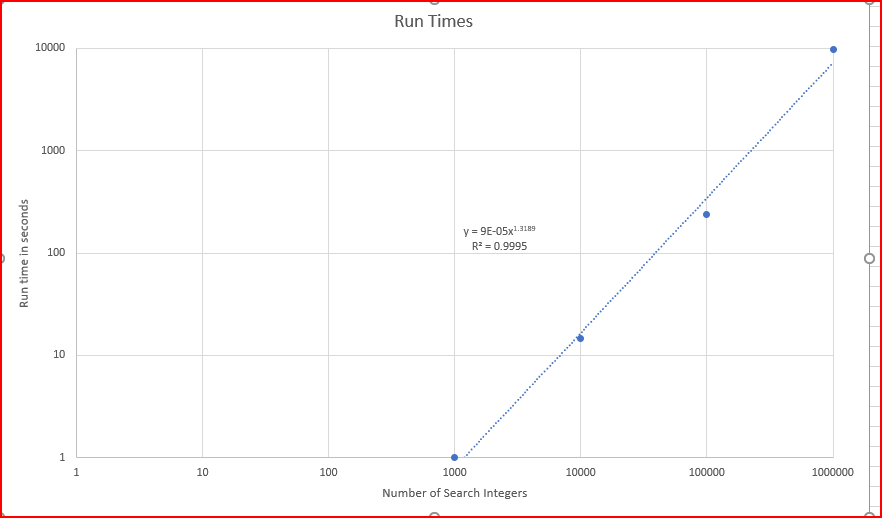
    end subroutine

The run times on a Core i7 with a lot of other stuff running in the background, are shown on the graph

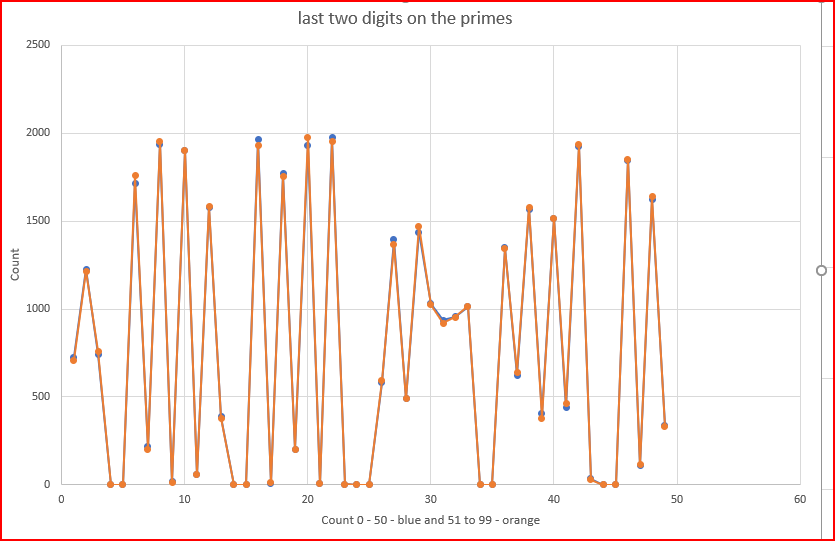
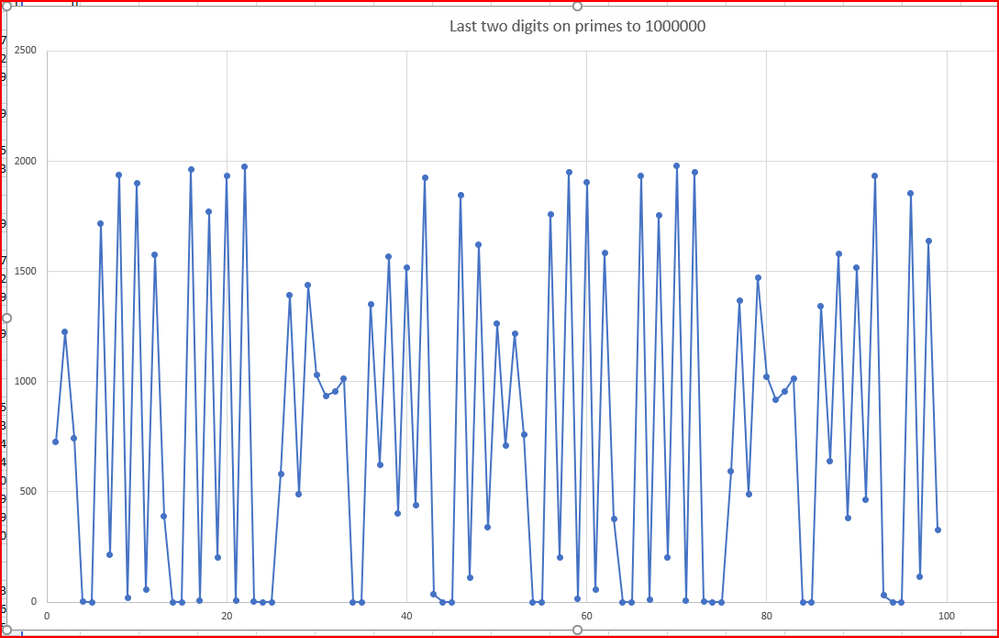
If you watch the prime numbers on the screen, it is not much faster to not print them out, you see the last two digits seem to repeat. I dropped off the last two digits and tallied them. They are consistent and the pattern of counts repeats pretty well with a cycle of 50.

The blue are 0 - 50 and the orange are 51 - 99, you can only just detect the blue, but it is there.

The problem with using integers to represent primes is you miss the beauty of these numbers.

Anyway it is just some fun.

JMN

andrew_4619 · ‎01-02-2022

format 110 and 111 have typo errors but it would be easier to just use i0 which writes the minimum characters

JohnNichols · ‎01-02-2022

Thanks, I was using *,* and the read did not like the large sets of blanks.

jimdempseyatthecove · ‎01-02-2022

On chart "Last Two DIgits..." why are all the even numbers not having 0 counts?

Jim Dempsey

JohnNichols · ‎01-02-2022

I did not notice that this morning, I will need to fix the algorithm. Thanks

JNichols · ‎01-03-2022

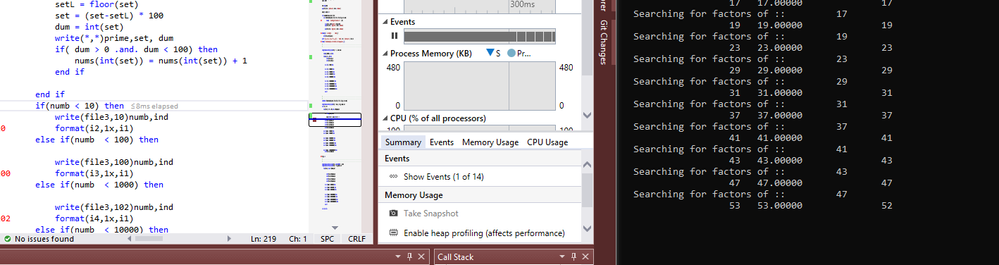
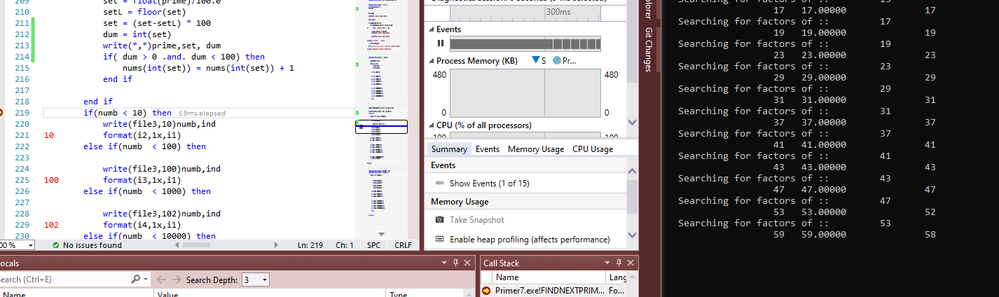
I was looking at the code again and running it on another computer. The command int() is doing some interesting things with the same numbers each time. I write out the prime number the set number the last two digits as a real and then the int(set) as dum and each time 53 comes out as 52,

58 did the same thing. Clearly the int is seeing 53.0000 as 52.99999 or something I realize it is binary so I need to amend the algorithm, not hard just annoying.

JohnNichols · ‎01-03-2022

dum = int(set + 0.001)

Fixed it.