- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi everyone!
I have been having problems with stack overflow error when I am trying to operate arrays through a function implemented in a module. The problem occurs only with arrays larger than 300x300.
I reduced and generalized the code to find where the error is and even then the problem reoccurs. I even compiled on two different computers with different versions of Visual Studio and Intel Parallel Studio and the error remains the same.
Has anyone experienced this same problem? What can I do to solve this error? Is there any compiler option to solve this problem?
The university computer that I am using has installed Microsoft Visual Studio Professional 2013 Update 3, Intel Parallel Studio XE 2016 Update 2 Cluster Edition for Windows.
I am using the following code to the main program:
program stack_overflow_error use mod_example_function implicit none ! Variables real(kind = 8), dimension(:,:), allocatable :: A, Afunc integer :: n, i, j ! Body of Matrix_inversion open(100, file='matrix300.txt', status='old') read(100,*) n allocate(A(n,n)) do i = 1,n read(100,*) (A(i,j), j = 1,n) end do allocate(Afunc(n,n)) Afunc = func(A) close(100) end program stack_overflow_error
and the following code to the module with the function:
module mod_example_function implicit none contains function func(A) result(Afunc) ! Variables real(kind = 8), dimension(:,:), intent(in) :: A real(kind = 8), dimension(size(A,1),size(A,2)) :: Afunc ! Body of FUNC Afunc = 0 Afunc = A end function func end module mod_example_function
Attached are the two txt files, one with an array 300x300 and the other with an array 400x400.
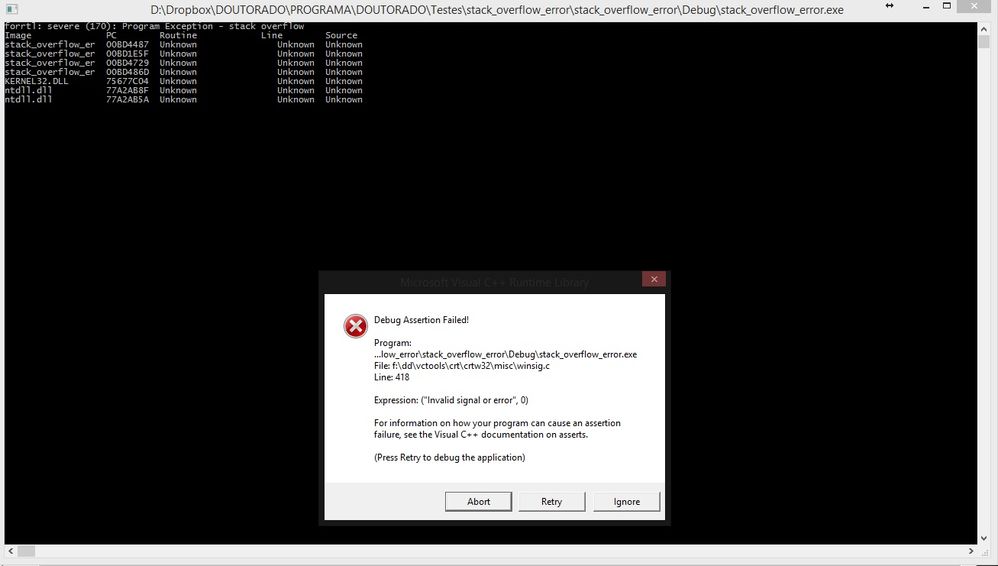
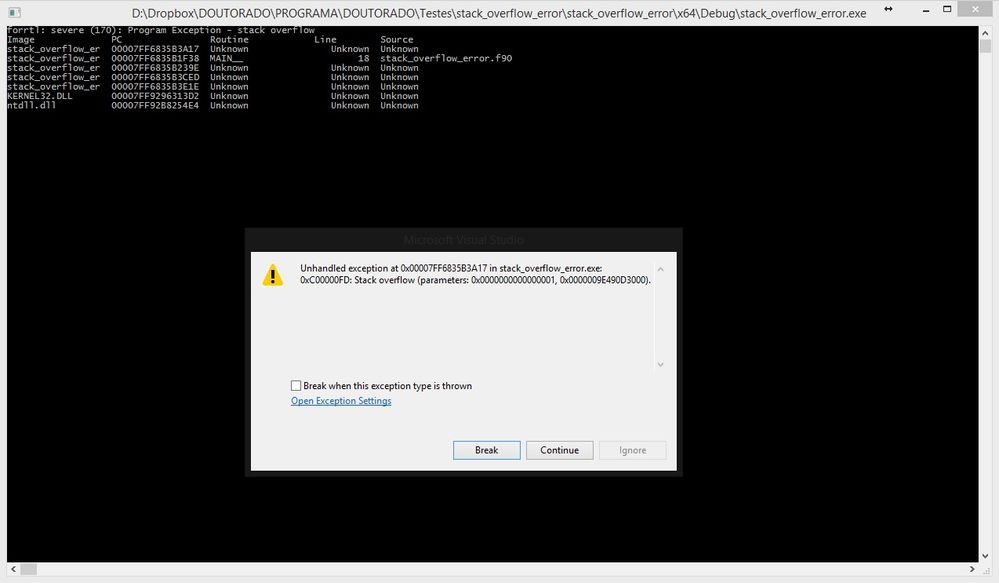
Attached are also two printscreens with the errors that appear when the program makes the operation with the array 400x400, one when is compiled in 32-bit and the other in the 64-bit.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Your function returns an array whose size is run-time dependent on the size of its argument. The compiler has to create space for this and does so on the stack by default. On Windows the stack is 1MB by default, so it's easy to overflow this.
The easiest solution is to set the project property Fortran > Optimization > Heap Arrays to 0. This will cause the array result to be allocated on the heap instead of the stack. Another choice is to set the Linker > System > Stack reserve size value higher. You may have to experiment to see what values work - don't make this much bigger than necessary.
I'll comment that the code you have shown is inefficient. First your "func" routine stores into the entire result twice, first with zero and then with the contents of A. The zero-fill is unnecessary. (Perhaps your actual program isn't like this.) Then the temporary function result is copied a third time to the allocated array in the caller.
Now I realize that what you have shown here is really a toy program meant to show the error. In real life - I hope - you would have just written Afunc=A in the main program and disposed of the function entirely, or maybe even written ALLOCATE(Afunc,SOURCE=A). But I'd also expect that the function did more than just copy its argument. You may want to consider replacing the function call with a subroutine call where you pass the destination as an argument.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you Steve!
Yes, I wrote this toy program trying to isolate and find out where was the error on my real program. In my real program I was following the idea of http://fortranwiki.org/fortran/show/Matrix+inversion to facilitate the use of DGETRF and DGETRI routines of LAPACK library for inverting matrices. First I thought the error was because of some limitation of routines DGETRF and DGETRI but reducing and isolating the error until I get the code lines that I posted I realize that the problem was not in DGETRF and DGETRI routines.
What I really need is an efficient routine to invert sparse matrices, so I was testing the limits of the function I had programmed to check if the efficiency was acceptable.
When I say I need a routine to invert matrices people think I need to solve linear systems of equations and there are more efficient routines for this, but I do not want to solve linear systems of equations. The problem I need to solve has a large sparse rectangular matrix with m rows and n columns where n is a large number of columns. I use on each iteration of my program a sparse square matrix with dimension m x m formed by the inverse matrix of m columns of the sparse rectangular matrix mentioned above. In each iteration a new column of the rectangular matrix is selected to be part of the square matrix and my program does all the necessary calculations to enter this new column.
The problem appears after several iterations where appears several numerical errors in the square matrix due to the iterative process. One way to clean these errors is to calculate the inverse matrix of all columns of the rectangular matrix that are being used in the square matrix.
Another error I have found is when I was trying to implement the functon of http://fortranwiki.org/fortran/show/Matrix+inversion, I tried to put this function in a submodule with the interface declared in the parent module. I could not do it because when I put the result statement the program simply did not compiled and also did not show why was not compiling it. Without the result statement occurred several other errors. What can be this error? Can I use the result statement in this situation?
Steve do you have any advice so I can improve the efficiency of my program?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You'd have to show me the actual code that gave you a compile error. It's possible we have a bug, or you missed something.
I can't make suggestions for improvements in code I have not seen. I always recommend running the program under VTune Amplifier XE and seeing where the hotspots are. Vectorization Advisor, part of Inspector XE, can make recommendations for improvements.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
>>What I really need is an efficient routine to invert sparse matrices
a a a a
b b
c c c
How do you intend to deal with the missing elements upon inversion? Are these to be 0.0, NaN, other?
Do you have sufficient RAM to un-sparsify?
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you Steve for your answer.
The following code is giving the error, this first is the main program:
program Matrix_inversion use mod_matrix_inversion implicit none ! Variables real(kind = 8), dimension(:,:), allocatable :: A, iA integer(kind = 8) :: n, i, j ! Body of MATRIX_INVERSION open(100 , file='inv300.txt', status='old') read(100,*) n allocate(A(n,n)) do i = 1,n read(100,*) (A(i,j), j = 1,n) end do allocate(iA(n,n)) iA = inv(A) close(100) end program Matrix_inversion
the module with the interface of the function:
module mod_matrix_inversion implicit none interface module function inv(A) result(invA) ! Variables real(kind = 8), dimension(:,:), intent(in) :: A real(kind = 8), dimension(size(A,1),size(A,1)) :: invA end function inv end interface contains end module mod_matrix_inversion
and finally the function that handles the DGETRF and DGETRI routines of LAPACK library:
submodule (mod_matrix_inversion) sub_inv implicit none contains module procedure inv ! Variables real(kind = 8), dimension(size(A,1)) :: work ! work array for LAPACK integer(kind = 8), dimension(size(A,1)) :: ipiv ! pivot indices integer(kind = 8) :: n, info ! Body of INV ! External procedures defined in LAPACK external DGETRF external DGETRI ! Store A in Ainv to prevent it from being overwritten by LAPACK invA = A n = size(A,1) info = 0 ! DGETRF computes an LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges. call DGETRF(n, n, invA, n, ipiv, info) if (info /= 0) then stop 'Matrix is numerically singular!' end if ! DGETRI computes the inverse of a matrix using the LU factorization computed by DGETRF. call DGETRI(n, invA, n, ipiv, work, n, info) if (info /= 0) then stop 'Matrix inversion failed!' end if end procedure inv end submodule sub_inv
This is the error message that appears trying to compile in 32-bit:
Compiling with Intel(R) Visual Fortran Compiler 16.0 [IA-32]... ifort /nologo /debug:full /Od /I"C:\Program Files (x86)\IntelSWTools\compilers_and_libraries_2016.2.180\windows\mkl\lib\ia32_win" /warn:interfaces /module:"Debug\\" /object:"Debug\\" /Fd"Debug\vc120.pdb" /traceback /check:bounds /check:stack /libs:dll /threads /dbglibs /Qmkl:parallel /c /Qlocation,link,"C:\Program Files (x86)\Microsoft Visual Studio 12.0\VC\\bin" "D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\sub_inv.f90" D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\sub_inv.f90(1): catastrophic error: **Internal compiler error: internal abort** Please report this error along with the circumstances in which it occurred in a Software Problem Report. Note: File and line given may not be explicit cause of this error. compilation aborted for D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\sub_inv.f90 (code 1) ifort /nologo /debug:full /Od /I"C:\Program Files (x86)\IntelSWTools\compilers_and_libraries_2016.2.180\windows\mkl\lib\ia32_win" /warn:interfaces /module:"Debug\\" /object:"Debug\\" /Fd"Debug\vc120.pdb" /traceback /check:bounds /check:stack /libs:dll /threads /dbglibs /Qmkl:parallel /c /Qlocation,link,"C:\Program Files (x86)\Microsoft Visual Studio 12.0\VC\\bin" "D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\Matrix_inversion_sub.f90" Matrix_inversion_sub - 1 error(s), 0 warning(s)
and this error message when compiling 64-bit:
Compiling with Intel(R) Visual Fortran Compiler 16.0 [Intel(R) 64]... ifort /nologo /debug:full /Od /I"C:\Program Files (x86)\IntelSWTools\compilers_and_libraries_2016.2.180\windows\mkl\lib\intel64_win" /warn:interfaces /module:"x64\Debug x64\\" /object:"x64\Debug x64\\" /Fd"x64\Debug x64\vc120.pdb" /traceback /check:bounds /check:stack /libs:dll /threads /dbglibs /Qmkl:parallel /c /Qlocation,link,"C:\Program Files (x86)\Microsoft Visual Studio 12.0\VC\\bin\amd64" "D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\sub_inv.f90" D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\sub_inv.f90(1): catastrophic error: **Internal compiler error: internal abort** Please report this error along with the circumstances in which it occurred in a Software Problem Report. Note: File and line given may not be explicit cause of this error. compilation aborted for D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\sub_inv.f90 (code 1) ifort /nologo /debug:full /Od /I"C:\Program Files (x86)\IntelSWTools\compilers_and_libraries_2016.2.180\windows\mkl\lib\intel64_win" /warn:interfaces /module:"x64\Debug x64\\" /object:"x64\Debug x64\\" /Fd"x64\Debug x64\vc120.pdb" /traceback /check:bounds /check:stack /libs:dll /threads /dbglibs /Qmkl:parallel /c /Qlocation,link,"C:\Program Files (x86)\Microsoft Visual Studio 12.0\VC\\bin\amd64" "D:\Dropbox\DOUTORADO\PROGRAMA\DOUTORADO\Testes\Matrix_inversion_sub\Matrix_inversion_sub\Matrix_inversion_sub.f90" Matrix_inversion_sub - 1 error(s), 0 warning(s)
I appreciate your analysis and your comments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Jim!
Currently I am dealing with zeros. I think for my final program I will not have problem with RAM.
I do not know but it would be nice if there were some routine that deal efficiently with inversion of sparse matrices as there is for solving linear systems of equations.
Do you know some routine that do this?
Thank you for your attention.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
No that it helps you much but "catastrophic error" is always a compiler bug so if you've got time it's worth reporting.
It looks as if you're currently using a slighty older version of the compiler (16.0). The current version is 16.0.3.207 and you might well find that the compiler bugs you're experiencing have been fixed so it it's possible to upgrade I'd recommend it.
Are you looking for efficiency in terms of time because an O(n**2) method is too slow for the size of your matrix. You could always roll your own version of Gaussian elmination which exploits the sparse structure of your matrix or would that still be too slow? How accurate does the result have to be? Is A ill-conditioned? Just some thoughts.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The compiler error might also go away if you 'use lapack95' rather than marking DGETRF and DGETRI as external.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the example - this has revealed a compiler bug that is still present in the latest compiler (as well as in the 17.0 beta.) I will escalate it to the developers. Unfortunately, using lapack95 doesn't make the bug go away.
The real trigger of the problem is defining the function return value with dimension(size(A,1),size(A,1)). None of the workarounds I tried resolved this. If you repeat the function declaration instead of using module procedure, the compiler then complains that the interfaces don't match when in fact they do. Issue ID DPD200413234.
The only workaround I can find is to not use a submodule for this. If the function is an ordinary module function it works.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you Steve for your review,
I was trying to use submodules to follow the same standard as the rest of my program, but because of this error I had given up using submodule for this function. When using this function as a module function that I found the stack overflow error for arrays with dimensions greater than 300x300.
You gave me three options to resolve the stack overflow error and at this point I'm more concerned with speed than with the memory consumption. Which of the three options would be most appropriate to ensure the speed?
In the properties of my project the option Fortran > Optimization > Heap Arrays is empty. The option Linker > System > Stack Reserve Size is equal to zero, I believe that I will not need to use arrays with dimensions greater than 1000x1000, which value would be appropriate for this option? This value must be added to B, kB or MB?
Thanks for your attention.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The empty value for Heap Arrays is the default, meaning it is disabled. If you want to enable this, put 0 in the value field. Other values are accepted but don't accomplish anything useful that 0 doesn't.
Your array has a million elements. Assuming they are four bytes each that's 4000000. I think 10000000 (10 million) is a reasonable starting point for stack reserve. This would be the higher performing option, though if you have that many elements I doubt you'd be able to measure the difference between stack and heap allocation.
If performance is paramount, you will want to avoid array temps (and copies) no matter where they are allocated. This will swamp the effect of how the temp is allocated. That may mean giving up array-valued functions and passing output arguments to subroutines instead. I wouldn't go there unless you're dissatisfied with the performance of the code as you have it - I always prefer clarity of code. You'll also want to take advantage of all the optimization features the compiler supports (/O3, /QxHost, parallelization, /Qipo, etc.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Simon Geard wrote:
No that it helps you much but "catastrophic error" is always a compiler bug so if you've got time it's worth reporting.
It looks as if you're currently using a slighty older version of the compiler (16.0). The current version is 16.0.3.207 and you might well find that the compiler bugs you're experiencing have been fixed so it it's possible to upgrade I'd recommend it.
Are you looking for efficiency in terms of time because an O(n**2) method is too slow for the size of your matrix. You could always roll your own version of Gaussian elimination which exploits the sparse structure of your matrix or would that still be too slow? How accurate does the result have to be? Is A ill-conditioned? Just some thoughts.
Thank you Simon for your comments,
About the version of the compiler I'm waiting for the university's IT department update to me.
I implemented my version of Gaussian elimination algorithms, but the implementation was not very effective because I had not considered the sparse structure. So I was looking for a library that could save me the trouble. The matrix inversion is not a fundamental part of my program I only use once every certain number of iterations to clear the numerical errors of the iterative process.
I started using in my program single-precision variables but I was forced to switch to double precision because the program did not converge after a few iterations. I also started using an acceptable error of 1E-5 , but when I switched to double-precision variables I changed the acceptable error to 1E-10.
I attached a small 36x84 matrix that I am using for testing. For this problem the first iteration of my program selects 36 columns of the matrix attached, thus forming a square matrix 36x36 that I must invert. After that, in each iteration is selected a new column of the matrix attached to be part of the square matrix. My program does all the calculations to insert these new columns in the square matrix.
After several iterations with much larger matrices than is attached my program begins to present numerical errors of the iterative process. So, I can eliminate these errors by inverting the matrix formed by the columns of rectangular matrix (such as that attached) that particular iteration.
I appreciate your analysis and your comments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you Steve for your tips,
I put "10000000" (10 million) in Linker> System> Stack Reserve Size and worked perfectly.
Once again thank you, I'll try to follow your tips.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The compiler bug (see #10) has been fixed for Update 1 to Parallel Studio XE 2017, planned for October.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page