- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
I started to investigate the possibility to use half precision for some mathematical routines.
However I found a suspicious high resource utilization when compared with classical floating point version.
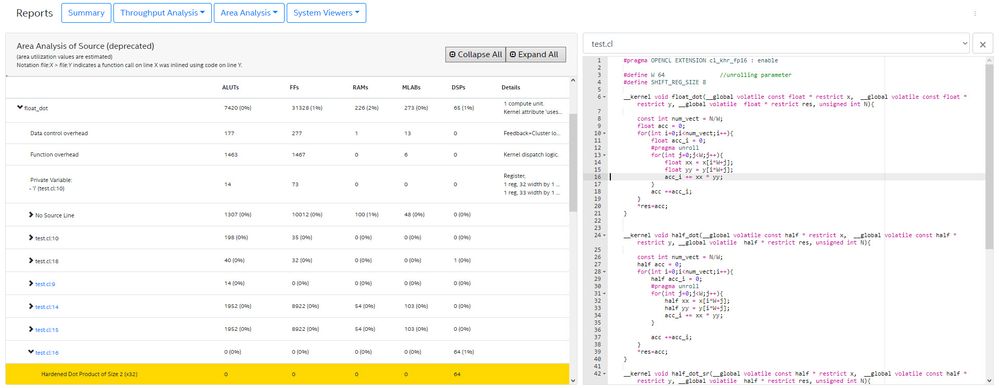
In the following code, there are three different implementation of a dot product, in which the computation is partially unrolled:
#pragma OPENCL EXTENSION cl_khr_fp16 : enable
#define W 64 //unrolling parameter
#define SHIFT_REG_SIZE 8
__kernel void float_dot(__global volatile const float * restrict x, __global volatile const float * restrict y, __global volatile float * restrict res, unsigned int N){
const int num_vect = N/W;
float acc = 0;
for(int i=0;i<num_vect;i++){
float acc_i = 0;
#pragma unroll
for(int j=0;j<W;j++){
float xx = x[i*W+j];
float yy = y[i*W+j];
acc_i += xx * yy;
}
acc +=acc_i;
}
*res=acc;
}
__kernel void half_dot(__global volatile const half * restrict x, __global volatile const half * restrict y, __global volatile half * restrict res, unsigned int N){
const int num_vect = N/W;
half acc = 0;
for(int i=0;i<num_vect;i++){
half acc_i = 0;
#pragma unroll
for(int j=0;j<W;j++){
half xx = x[i*W+j];
half yy = y[i*W+j];
acc_i += xx * yy;
}
acc +=acc_i;
}
*res=acc;
}
__kernel void half_dot_sr(__global volatile const half * restrict x, __global volatile const half * restrict y, __global volatile half * restrict res, unsigned int N){
const int num_vect = N/W;
half shift_reg[SHIFT_REG_SIZE+1]; //shift register
#pragma unroll
for(int i=0;i<SHIFT_REG_SIZE+1;i++)
shift_reg[i]=0;
half acc = 0;
for(int i=0;i<num_vect;i++){
half acc_i = 0;
#pragma unroll
for(int j=0;j<W;j++){
half xx = x[i*W+j];
half yy = y[i*W+j];
acc_i += xx * yy;
}
shift_reg[SHIFT_REG_SIZE] = shift_reg[0]+acc_i;
#pragma unroll
for(int j = 0; j < SHIFT_REG_SIZE; ++j)
shift_reg[j] = shift_reg[j + 1];
}
//reconstruct the result using the partial results in shift register
#pragma unroll
for(int i=0;i<SHIFT_REG_SIZE;i++)
acc+=shift_reg[i];
*res=acc;
}
- float_dot: classical floating point version. It takes advantage of the single clock cycle accumulator, obtaining an II=1
- half_dot: simple version using half instead of float. In this case, single clock cycle accumulator is not used, resulting in an II=3
- half_dot_sr: a shift register has been introduced to mask loop carried dependency, obtaining an II=1
Apart from the single clock cycle accumulation, is there any good reason about the fact that half precision versions use much more logic resources compared to the floating point version (~10X LUTs and ~3x FFs)?
This has been evaluated using Quartus 19.1.0, targeting a Stratix 10.
Thanks for the help
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
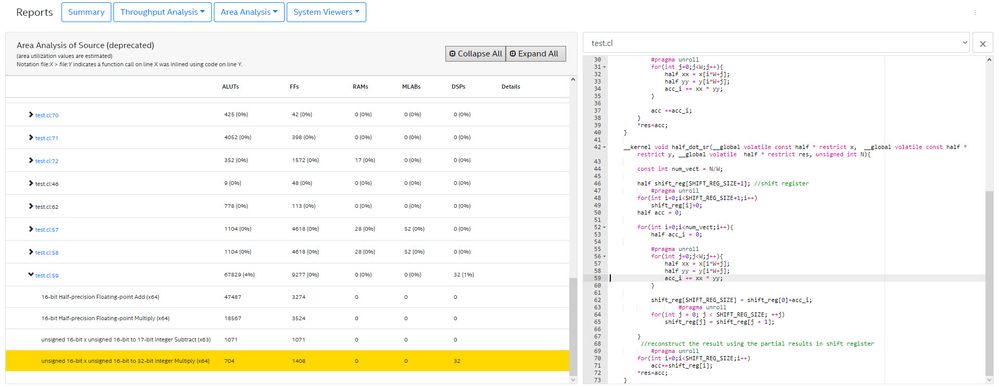
The DSPs in Stratix 10 do not natively support FP16 (half-precision) computation, while they natively support FP32. When you use FP32, all the computation is performed within the DSP and little logic is used outside of the DSP. In fact, for FP32, a full FMA (a.k.a. MAC) operation can be performed with each DSP. For FP16, however, only the multiplication of the mantissa is offloaded to the DSP and every other operation has to be done using logic. For the particular case of FP16 addition, DSPs are not used at all and the operation is completely offloaded to logic. This is shown clearly in the are report.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the quick reply.
>>> This is shown clearly in the are report.
I guess it is what "Implemented using inlined soft-IP" means.
Therefore, should I conclude that if I have a compute intense half-precision routine (e.g. GEMM), it is better in terms of performance/resource usage to implement it using classical FP32 (or to cast the loaded numbers to fp32)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Sorry, I had a typo in my original post, I meant the "area report":
On Arria 10 and Stratix 10, FP32 performance will likely be higher than FP16 in general, unless your application is memory-bound (which is actually quite likely considering how low the external memory bandwidth of typical FPGA boards is). If you don't need floating-point and fixed-point/integer can be enough for your application, then you can do a full (a * b) + (c * d) with one DSP if your data type size is 18 bits or less and achieve higher computational performance than FP32. Next generation Intel Agilex will have native support for FP16 in the DSPs.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page