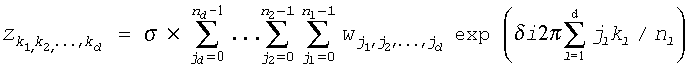- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
I am attempting to test my FFT routines with known solution transforms, and the results that I have been getting are not what is expected. In order to maintain generality for my final implementation, the FFTs are being computed as complex-to-complex and out-of-place. The input I have tested is as follows:
- Forward transform of an array populated with complex number (1,0). The result should be DiracDelta(w) (up to a constant, anyway), and therefore should have purely real output which is zero everywhere but spiked at w=0. Instead, I get output with a spike in the reals at w=(far left of data set).
- Backward transform of DiracDelta( w-1.5 ). This should result in (again to a constant) Cos(1.5 t) - iSin(1.5 t). I instead get complex output oscillating with an extremely small period (on the order of w=10^-3 instead of the expected w=1.5) in both real and imaginary domain.
- Backward transform of a narrow Gaussian, instead of a hard delta spike in #2, just in case the method didn't like that. Got the same results as #2.
I have been struggling with this issue for a few weeks now, and any help would be greatly appreciated. My codes are attached. The external module bremModule.f90 contains the functions for running the FFTs, while ffttest.f90 contains the input array initialization, function calls, and I/O control.
Thank you.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Andrew,
Your test fails because of non-zero based arrays.
Intel MKL supports only zero-based arrays -- please read top of https://software.intel.com/en-us/node/521955.
Evgueni.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Due to the periodic nature of the time domain, the following is the correct way to go from [0,nLength-1] to [-nLength/2,nLength/2-1] in FFTs.
do j=-nLength/2,nLength/2-1 write(15,*) j*dn,real( nListIn (mod(j+nLength, nLength)) ) write(16,*) j*dn,real( nListOut(mod(j+nLength, nLength)) ) write(17,*) j*dn,imag( nListOut(mod(j+nLength, nLength)) ) end do
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
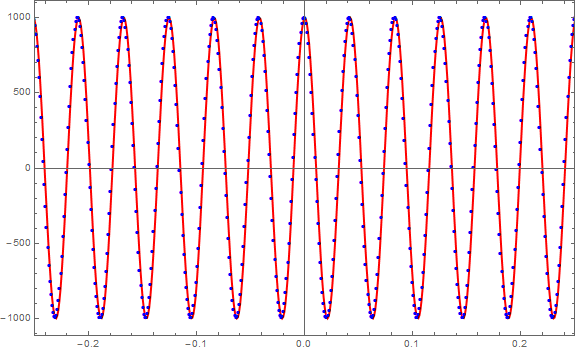
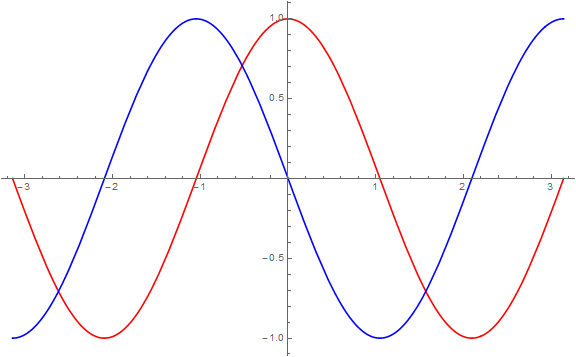
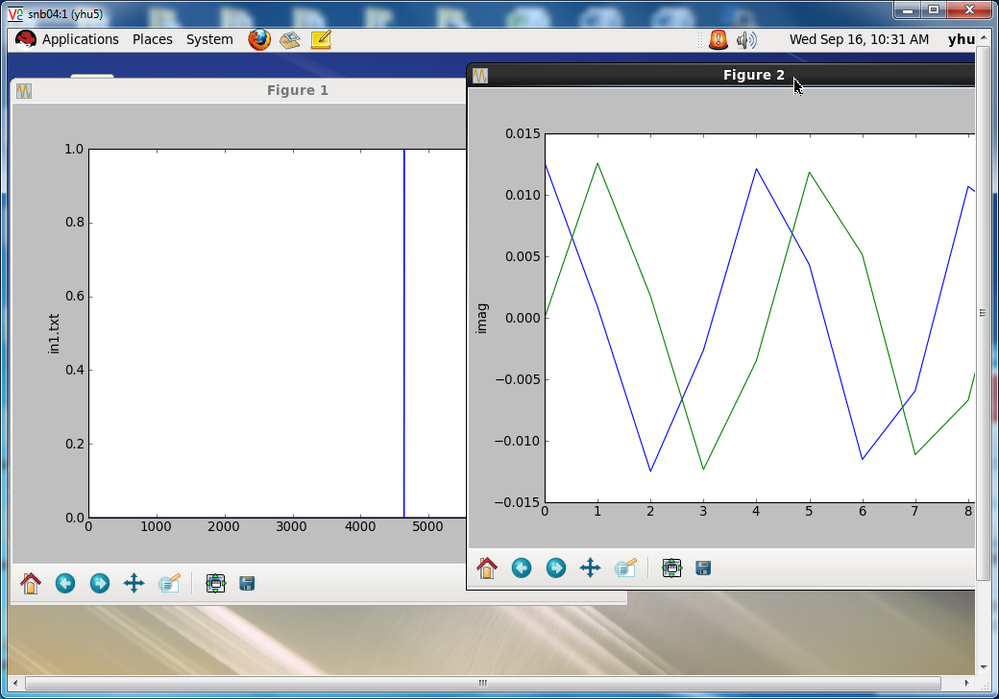
Thanks, that helped move things in the right direction. Something is still wrong, though. Using the backward transform of input DiracDelta(w-1.5), we would again expect real Cos and negative imaginary Sin of frequency 1.5. The input plots correctly, however, as you can see in the following plot of the results of the transform, the output is incorrect. The frequency is clearly higher than 1.5, and the real (red) and imaginary (blue) parts are almost completely in-phase instead of the expected out-of-phase behavior.
This is what it should look like:
The up-to-date code is attached.
Also, on Intel's page of MKL FFT examples (link here), the arrays are shown as being one-based. The FORTRAN standard convention is that "arrayName(length)" gives entries at arrayName(1)...arrayName(length). This seems to contradict what you mentioned about MKL FFTs only supporting zero-based arrays. Could you please clarify this for me?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
In order to see in the picture that real and imaginary parts do have different phase, you need to scale the output. So you should change dcmplx(1.d0/dn,0.0d0) to dcmplx(1.d0,0.0d0), or set backward scale via DFTI explicitly because, by default, Intel MKL FFTs do not scale output; neither forward, nor backward.
The frequency is higher than 1.5 because ffttest.f90 says "nmax=3.14*10" instead of "nmax=3.14".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the response Evgueni, but I do not understand what you have just told me:
- From what I read about the parameter DFTI_FORWARD_SCALE (source), this has to do with a complete re-scaling of the magnitude of the output of the transform (the 1/(2*pi) factor in the standard FT formulation, for example). What effect would this have on phase, and how?
- In my code, "nmax=3.14*10" is defining the length of the I/O arrays to be 10 cycles of Sin(x). In the case of the Delta input, this just means more zero-valued space on either side of the spike at w=1.5. The location of this spike in w-space is what dictates the period of the oscillations, not the input array's length.
- Also, please still clarify the point on zero- or one-based arrays per my last post.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Without scaling, the size of your plot is 0.5 by 2000 units and the phase difference is hard to see because it plots as one pixel or less.
- By definition of discrete Fourier transforms, the input array contains only one cycle.
- In Intel MKL, forward transforms store the coefficient of the zero-frequency harmonic at the smallest memory address in the output array, regardless of the smallest index in the FORTRAN declaration. For academic people, this fact means that Intel MKL supports only zero-based arrays in descrete Fourier transforms -- hence my answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Per your suggestions, I changed the forward/backward scaling each to 1/sqrt(nLength), and changed "nMax=3.14*10" to "nMax=3.14". While scaled down, the output is still scaled a factor of 10 larger than it should be, and the frequency of final oscillations is even higher than it was previously. The phase difference is still not seen on this smaller scale.
Also, I still do not understand what you said about the input array containing only one cycle. In this case, the input array represents a Dirac Delta function. This is not a periodic function, therefore has no defined cyclic period. In general, in my final implementation, I will not know what the input or output arrays "look like". As such, how would I know a priori how long to make my input array such that it is the proper length to be accepted by the MKL DFFT?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Andrew,
The FFT function follow the math formula. fhttps://software.intel.com/en-us/node/521955
or kl = 0, ... nl-1 (l = 1, ..., d), where σ is a scale factor, δ = -1 for the forward transform, and δ = +1 for the inverse (backward) transform. It is 0-based, may be not align exact with FFT standard formula.
So you may align your input with the asked input
1) Input index: for example, it is 0-based in formula, where fortran array from 1 by default. but change it's define from 0 nListIn(0:nlength))
2) magnitude
The forward transform and backward transform are each associated with a scale factor σ of its own having the default value of 1. You can specify the scale factors using one or both of the configuration parametersDFTI_FORWARD_SCALE and DFTI_BACKWARD_SCALE. For example, for a one-dimensional transform of length n, you can use the default scale of 1 for the forward transform and set the scale factor for the backward transform to be 1/n, thus making the backward transform the inverse of the forward transform.
so if you want get exact forward array, teh backward scale should be 1/n.
3) about periodic,
as math, the FFT is integration. but when calculate as Discrete Fourier Transfrom , the input arrary is limitation. so whatever input is from , we take FFT /IFFT's input is one cycle of one unlimited periodic array. So you may shift the input or output to get what you expect to see.
Best Regards,
Ying
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Regarding Ying's responses:
1) My arrays are defined as zero-based.
2) My forward and backward scales are each set at 1/sqrt(n). This should give the proper scaling in a forward/backward cycle, but it does not.
3) I still don't understand how to pick the "one cycle" for the input array when the input is not periodic (such as with the delta function), or in general when you don't know what your input "looks like". What is the highest level generalization of acceptable input length and start point?
My code is again attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Andrew,
Regarding the frequency of the Backward Fourier Transform (BFT):
In your last ffttest.f90, you want to do BFT of DiracDelta(w-1.5).
First, according to the DFT math formula shown above, the frequency of the result should be 1.5*2π instead of 1.5, which means that the period should be 0.667 instead of 4.19.
Second, in order to see the correct frequency, you need to write your results as
do j=-nLength/2,nLength/2-1
write(15,*) j/6.28,real( nListIn (mod(j+nLength,nLength)) )
write(16,*) j/6.28,real( nListOut(mod(j+nLength,nLength)) )
write(17,*) j/6.28,imag( nListOut(mod(j+nLength,nLength)) )
end do
Hope this helps.
If the the real and imaginary part still have the same phase, then I don't know why is that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
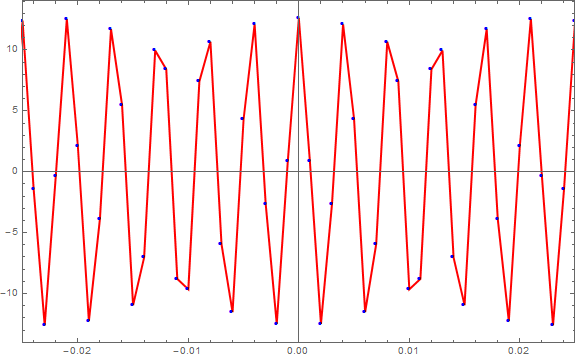
Thank you Dian, making that change does indeed modify the period of the transformed data as you predicted to ~0.667.
The phase difference and scaling are still off though, so if Evgueni or Ying have any further information about those points it would be appreciated. If you still think that the input array's length has something to do with these issues, please generalize the relationships between input array length and related variables for me.
Thanks,
- Andrew
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Andrew,
Regarding the phase and scaling issue, the main problem seems in the code ffttest.f90
if (j*dn.eq.1.5) then
It is floating point type. You can't use the eq to compare the floating point number.
So yu may change them to integer
if (j .eq.1500) then
or other way to set the DiracDelta(w-1.5).=1 or 1/dn , to see if there are changing on phase.
Best Regards,
Ying
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
A quick test indicates that my comparison with .eq. is working fine. In ffttest.f90, I modified the statement in question:
if (j*dn.eq.1.5) then
print*,"j*dn=",j*dn,"=1.5" <--- added this line
nListIn(mod(j+nLength,nLength))=dcmplx(1.d0/dn,0.0d0)
...
Then, my .out file contains the new line
j*dn= 1.50000000000000 =1.5
Thus, since this is the only new output line, we can see that the numbers are indeed being compared correctly. This is further seen in my previously posted plots of the input data, where the delta spike is clearly visible at 1.5 in omega-space.
The only time that .eq. would be risky with floating point numbers is if we had to deal with potential round-off errors, but given that I have defined an exact step size this is never an issue that would arise in this code.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Andrew,
Right It is risky to do floating comparing like this, although it may be right in current case. Anyway, please check you input data, and output data.
for example, let nListIn(6280-1500) = 1 and see the result.
Regards,
Ying
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page