Intel MKL _feast eigensolver problem

[zhang__boyuan]

Hi community,

I'm tring to use the zfeast_hcsrgv solver to solve a generalized eigenvalue problem of the following format:

M*v = lambda*B*v

where M is a hermitian matrix.

The problem I'm solving is finding the electromagnetic eigenmodes using finite difference method. As for the simplest case in vacuum, the matrix M is a sparse one and B is a diagonal with constant diagonal entries in it. 

Suppose the mesh size of the calculation domain is N by N by N, and therefore the size of matrices M and B is  N^3 by N^3. At the beginning I used a small mesh size, and I could run the zfeast solver and get correct results. However, when I used a finer mesh, the solver exited with the following message:

Intel MKL Extended Eigensolver WARNING: No eigenvalue has been found in the proposed search interval.

INFO code =: 1

Essentially, by using a finer mesh, the mesh size N is increased and so is the matrice size. In addition, the non-zero elements in M is inversely proportional to mesh size, thus a finer mesh makes the non-zeros in M larger. The non-zeros in B is unchanged.

Based on this, I suspect that the failure of the eigensolver is due to the large difference in magnitude order between non-zero elements in M and B. I tried to scale the eigenvalue problem by divide a scale factor to M, but either the solver still fails, or it takes forever to complete the iteration.

Could anyone give me any suggestions on how to fix this problem? Any kind of feedback would be greatly appreciated.

Thanks in advance!

Sincerely,

Boyuan

[Gennady_F_Intel]

how could we check the behaviour on our side?

[zhang__boyuan]

Hi Gennady,

Thanks for the reply. My code for generating the M matrix is pretty long, so I attached the data files instead.

The mesh_20 file is the case where the mesh size is 20 by 20 by 20, while the mesh_25 case is with mesh size 25 by 25 by 25.

In both cases, B.dat , B_ iIndex.dat, B_ jIndex.dat are the non-zero entries, their row indices and their column indices in matrix B, respectively.

M_real.dat, M_imag.dat, M_iIndex.dat, M_ jIndex.dat are the real part and imaginary part of the non-zero entries, their row indices and their column indices in matrix M, respectively.

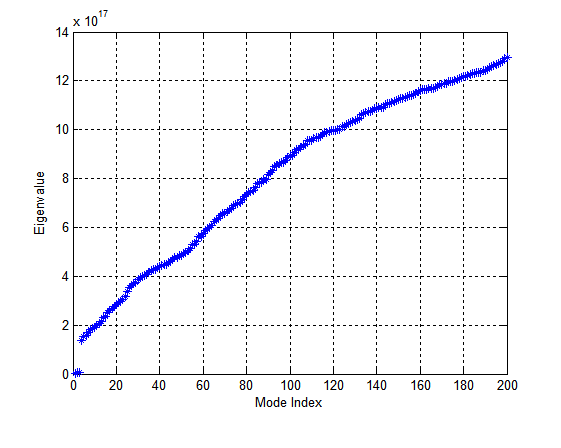
For the mesh_20 case, I can get the correct eigenvalues, which is shown in the figure below:

The input search range for the eigenvalues is [4*pi*pi*1e14, 4*pi*pi*2e16], and the input number of eigenmodes M0 = 200. The input parameter vector fpm is set as:

fpm[0] = 1;
fpm[1] = 8;
fpm[2] = 12;
fpm[3] = 20;
fpm[6] = 5;
fpm[26] = 1;
fpm[27] = 1;

with other elements being 0.

The matrix type is 'full'. The size of the matrix is nsize = 3*20*20*20 in the mesh_20 case, and nsize = 3*25*25*25 in the mesh_25 case.

With the same input parameters (except nsize), the zfeast_hcsrgv in the mesh_25 case exits almost instantaneously with no eigenvalues can be found in the search interval warning message.

Please let me know if there is any other information you need to reproduce these two cases.

Best regards,

Boyuan