- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I think LAPACKE_zgesvd has a bug.
When I use this function to calculate the SVD of a 2*1 matrix [1;3], the result seems to be wrong.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Since you are using the LAPACK_ROW_MAJOR convention, the value passed for ldA should be n, not m. Many C users make this mistake and I think that the imprecise description in the MKL documentation contributes by using the term "leading dimension" in an inappropriate way.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Please show us the result, and tell us why it "seems to be wrong".
I tried the same 2 X 1 matrix example with MKL 11.1 and 11.2, and the results agreed with those from Matlab.
Given that your matrix is real, why do you call the complex SVD routine?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your reply!
Do you use LAPACKE_zgesvd to calculate?
So you mean with different data type, we must use corresponding function. I can not call complex SVD routine when I use real matrix.
Oh, I think that's the problem. I always treat the real number as a special case of complex number and I just let the imaginary part to be 0 to call the complex routine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Chunyu W. wrote:
Do you use LAPACKE_zgesvd to calculate?
Yes. I used a modified version of the file lapacke_zgesvd_row.c that is distributed in the examples subdirectory of MKL.
So you mean with different data type, we must use corresponding function. I can not call complex SVD routine when I use real matrix.
You should know the properties of the three matrices that the SVD produces. If the original matrix is real, the U, S and VT matrices are all real. When the routines to handle this case (sgesvd and dgesvd) are provided, why would you resort to using the more general routine for complex matrices? All the imaginary parts in the results will be zero, and the calculation will be much slower, without any purpose.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I still think that complex SVD routine can calculate real matrix and it should be compatible with real matrix.
I use LAPACKE_zgesvd because sometimes I get complex matrix and sometimes I get real matrix, so I call this function overall, you know it is troublesome to judge what matrix I get.
I think the problem might have something to do with the superb parameter.
Below is an explanation about superb from the documentation(https://software.intel.com/sites/products/documentation/hpc/mkl/mklman/)
On exit, superb(0:min(m,n)-2) contains the unconverged superdiagonal elements of an upper bidiagonal matrix B whose diagonal is in s (not necessarily sorted). B satisfies A = u*B*vt, so it has the same singular values as A, and singular vectors related by u and vt.
So my question is that when min(m,n) = 1, what should be the size of superb? This is just the case when I caculate [1;3].
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Chunyu W. wrote:
I think the problem might have something to do with the superb parameter.
Since you have not yet stated what exactly the problem is, I cannot comment on that. The matrix B is of the same size as S. However, S is diagonal whereas B is upper bi-diagonal.
In your example, S is 1 X 1, so the size of the first upper diagonal is zero. However, C does not allow you to declare an array of size zero, so you could declare "double superb[max(1,min(M,N)-1)]. Alternatively, pass NULL as the last argument to LAPACKE_zgesvd.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your patience!
I might paste my code here as well.
/**********************code*******************************/
void svd(int m, int n, FemasDComplex * a, FemasDComplex * u, FemasDComplex * vt, double * s, double * superb)
{
(void)LAPACKE_zgesvd(LAPACK_ROW_MAJOR, 'A', 'A', m, n, (MKL_Complex16 *)a, m, s, (MKL_Complex16 *)u, m, (MKL_Complex16 *)vt, n, superb);
}
int _tmain(int argc, _TCHAR* argv[])
{
FemasDComplex a[2], u[4], vt[1];
double s[1];
a[0].real = 1;
a[0].imag = 0;
a[1].real = 3;
a[1].imag = 0;
for(int i=0; i<2; i++)
cout<<a.real<<'+'<<a.imag<<"i\n";
cout<<endl;
svd(2, 1, a, u, vt, s, NULL);
//print the result
cout<<s[0]<<endl;
for(int i=0; i<4; i++)
cout<<u.real<<'+'<<u.imag<<"i\n";
cout<<endl;
for(int i=0; i<1; i++)
cout<<vt.real<<'+'<<vt.imag<<"i\n";
cout<<endl;
while(1);
return 0;
}
/****************************code*******************************************/
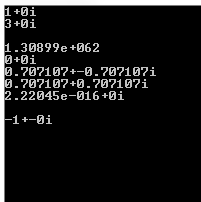
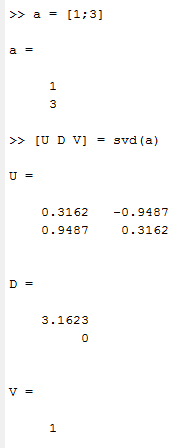
above is c++ result
above is matlab result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
FemasDComplex is a structure the same as MKL_Complex16.
typedef struct FemasDComplex {
double real;
double imag;
} FemasDComplex;
I test some other matrix, they give the same result as matlab, just this one show a different result. [1 ; 3]
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Since you are using the LAPACK_ROW_MAJOR convention, the value passed for ldA should be n, not m. Many C users make this mistake and I think that the imprecise description in the MKL documentation contributes by using the term "leading dimension" in an inappropriate way.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you. That's exactly the reason.
I also notice that svd is not unique actually, so it is sometimes possible that the result may not be the same as matlab.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page