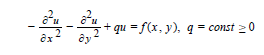- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I am trying to model a packed bed reactor with a system of three or four partial differential equations and Ordinary Differential Equations(momentum, energy and mass continuity equations). Does any know of any subroutines, either in the MKL library or eslewhere free which can do this for me ? Any solutions for C/C++ as well as for Fortran would be welcomed.
Regards
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Jason,
MKL provide 2 kind PDE solver, you may refer to MKL referenance manual at https://software.intel.com/en-us/node/521730 of https://software.intel.com/en-us/articles/intel-math-kernel-library-documentation
The Intel® Math Kernel Library (Intel® MKL) provides tools for solving Partial Differential Equations (PDE). These tools are Trigonometric Transform interface routines (see Trigonometric Transform Routines) and Poisson Solver (see Fast Poisson Solver Routines).
and please see at the what if experimental software site :http://software.intel.com/en-us/whatif/You can find there link to the ODE Solver -Intel Ordinary Differential Equations Solver Library
Best Regards,
Ying
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks
These are for solving single PDEs, what about solving them simultaneously
Regards
Jason
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Jason
If you wanted to solving them simultaneously, you may add some external thread on those single PDEs. For example, OpenMP pragma
https://software.intel.com/en-us/node/528550
!$OMP PARALLEL DO SHARED(len, x) PRIVATE(myStatus)
do th = 1, nth
myStatus = PDE (x(:, th))
end do
Best Regards,
Ying
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Ying
I do not understand your comment
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Jason,
MKL are threaded internally by OpenMP thread. ( latest version, TBB threading was added). for example,
Functions Threaded with Intel® Threading Building Blocks
In this section, ? stands for a precision prefix or suffix of the routine name and may have the value of s, d,
c, or z.
The following Intel MKL function domains are threaded with Intel® Threading Building Blocks (Intel® TBB):
• LAPACK:
For a list of threaded routines, see LAPACK Routines.
• Entire Level3 BLAS
• Fast Poisson, Laplace, and Helmholtz Solver (Poisson Library)
• PARDISO - Parallel Direct Sparse Solver.
For details, see PARDISO Steps.
Which mean when you call such functions, they will run in multi-threads on multi-core machine automatically. (especially, for the linear solver like AX=b, b can be multiply right hands vector, lay say B(b1, b2, ..). which are threaded too in MKL function internally. )
Could you please explain, what purpose for the question "These are for solving single PDEs, what about solving them simultaneously"
In general, if you want to solve multiply PDE simultaneously, and internal threads are not wanted, then you may use external threads to call them.
Best Regards,
Ying
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Ying
Sorry for the late reply. I should be more specific. I am trying to trying to use finite difference methods to solve heat and mass balances.
I have seen from the MLK library that you have the various solvers. Hemholtz, etc. However my problem is that from the appearance.
The coefficients of the first two terms on the left hand side must be equal to 1. The equations I want to use look similar to what is shown below.
![]()
The core equation is similar but the coefficients are different. Have you ever encountered this situation before.
Regards
Re
![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
HI,
I am trying to solve the diffusion type equation with periodic condition in X and Y and Neumann Condition in the Z direction and facing couple of problems. First of all if i take the BC TYPE as 'PPPPNN ' and specify the Z boundary as bd_az[]= 0.0 and bd_bz[]= 0.0, Will it take the zero Neumann Condition at the boundaries automatically or i am doing something wrong?
And the second question is if i write the diffusion equation in terms of Poisson equation then my RHS or the 'f ' becomes the time dependent part (du/dt), Will it create any problem because what i think is that it is becoming a mixture of different time schemes ?
Or is there any other method to solve time dependent equation using the Poisson solver with those specified boundary conditions ?
It will be very helpful if someone can provide a proper explanation..
Thanks,
Swagnik
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page