- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Steve:
I have stumbled into this interesting problem - I need to invert a large (5000 by 5000) sparse matrix.
Clearly I am going to use MKL but I have not played previously with sparse matrices. The numbers are straightforward doubles.
Which is the best routine to call and what is the best method to create a sparse array - about 10% density is my guess?
regards
JMN
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Is the matrix banded, or is the distribution of non-zero elements more disorganized? Secondly, whether the matrix is sparse or not, there is almost never a need to invert a matrix and store the inverse explicitly. Please expand on what you plan to do with the inverse.
MKL is rich in methods for solving sparse matrix problems (solution of equations, least squares, eigenvalues, singular values,...).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The problem is the usual Ax = B, where A is n by n, x is n and B is n
I am only interested in getting the Soln x.
The problem is likely to be banded heavily
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
They have got you covered. The easiest to use is GBSV from the lapack95 library. There is an example, gbsv.f90 and gbsv.d, packed into the zip file examples_f95.zip in the .../mkl/examples directory of your Intel Fortran installation. If you are not already familiar with the banded matrix storage format, you can read the section "Matrix Arguments" in the MKL reference manual.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
As mecej4 pointed out, GBSV can be used to solve a banded matrix A with multiple right-hand sides. Note that GBSV supports more than just LAPACK95 interface. It also has Fortran 77 and C (that is LAPACKE) interfaces. See more here: https://software.intel.com/en-us/node/520976
If your sparse matrix is not strictly banded then you should consider using the PARDISO sparse solver: https://software.intel.com/en-us/node/521677
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I decided to try the PARISO routine for the first go.
I have the latest Fortran compiler and MKL from a few weeks ago. I set the MKL vars to 64 bit.
I linked in the MKL library in the Project Properties
I copied one of the spares matrices from the Intel Page that describes how to code sparse matrices
It seemed to compile ok after I created all the arrays etc. but I get the following output - attached as a capture.png.
I am not sure what the error codes mean?
JMN
Console1.f90 ! ! FUNCTIONS: ! Console1 - Entry point of console application. ! !**************************************************************************** ! ! PROGRAM: Console1 ! ! PURPOSE: Entry point for the console application. ! !**************************************************************************** program Console1 implicit none integer pt(64) integer maxfct integer mnum integer MTYPE integer phase integer n integer perm(64) integer iparm(64) real a(25) integer ia(25) integer ja(25) integer nrhs integer msglvl real b(25) real x(25) integer error ! Variables ! Body of Console1 print *, 'Hello World' maxfct = 1 mnum = 1 MTYPE = 11 phase = 331 n = 5 iparm(1) = 1 a(1) = 1 a(2) = -1 a(3) = -3 a(4) = -2 a(5) = 5 a(6) = 4 a(7) = 6 a(8) = 4 a(9) = -4 a(10) = 2 a(11) =7 a(12) =8 a(13) =-5 ia(1) = 1 ia(2) = 2 ia(3) = 4 ia(4) = 1 ia(5) = 2 ia(6) = 3 ia(7) = 4 ia(8) = 5 ia(9) = 1 ia(10) = 3 ia(11) = 4 ia(12) = 2 ia(13) = 5 ja(1) = 1 ja(2) = 4 ja(3) = 6 ja(4) = 9 ja(5) = 12 ja(6) = 14 nrhs = 1 msglvl = 1 call pardiso (pt, maxfct, mnum, mtype, phase, n, a, ia, ja, perm, nrhs, iparm, msglvl, b, x, error) end program Console1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi John ,
It seems you called phase =331, the phase 1 and 2 was missed as the article
https://software.intel.com/en-us/articles/find-solution-to-input-error-in-pardiso
mentioned:
check Points 2: PARDISO Solver Phases
Usually, Intel MKL PARDISO solver performs four phases in succession:
-analysis and symbolic factorization (phase=1)
-numerical factorization (phase =2)
-forward and backward substitution including iterative refinement (phase =3)
-termination to release all internal solver memory (phase = -1 or 0)
As PADISO solver is used in iteration often or wrapped by other code, the phase =1 and phase =2 may be missed incorrectly some times. For example, with the test code in U489205, if the phase 1 and phase 2 were missed. The error Error in PARDISO ( sequence_ido,parameters) error_num= 8 shows up
Best Regards,
Ying
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
John, you have a number of errors in your program.
1. Set phase = 13 if you want to do the whole solution in one swoop. You cannot jump in with phase = 331 without doing the required earlier phases in prior calls.
2. You have the ia and ja arrays switched.
3. You have not assigned values to the b array (in A x = b) before calling Pardiso.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dear Guys:
Thanks for the reply.
So PARDISO is a looped program, one can use it multiple times - hence the term phase, interesting turn of phrase.
I will do the switches, and set the b matrix. I knew I had not set the b, but I tried it each time I put in a variable to see what errors I kept getting.
I have been playing with some water supply analysis code - from the EPA. I am using the oldest version, just for fun really and I had translated it to C# to see if I could run it from inside AutoCAD. The data is in AUTOCAD and taking it out us a pain, so running directly against the data was a challenge.
I had coded the original solver from the original program (old fashioned C - which will not compile in the current VS Studio 2013) so I made sure I had the algorithm correct and then looked to substitute a solver. I tried the MathNet solver and it solves the A matrix in X cubed time. MathNet can call the MKL libraries, but it is not nice, so I am going the direct route to improve the solution time.
JMN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Dear Guys:
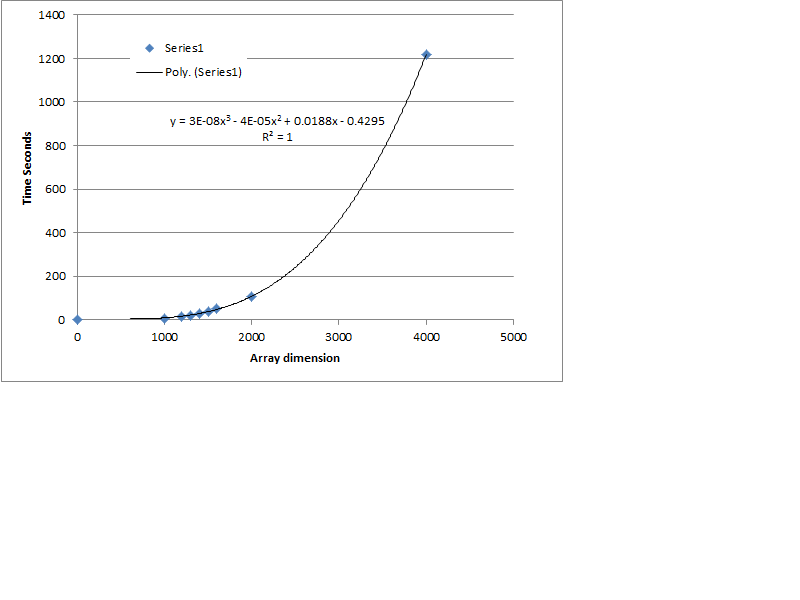
It ran nicely and I got a solution time of 3.7 milliseconds - it is 3 times faster than the MathNet code on a Dell Laptop Precision.
I enclose the graph of the MathNet solver times:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The problem with the cubic equation is that for small array sizes the solution time is essentially linear - which is ok who cares, for intermediate arrays it is parabolic and so a small town with a 1000 node network has a shortish solution time, but by 4000 ( College Station size) nodes it is a long run time. I can make a cup of tea time, which reminds me of the compile time on the original COMPAQ portable - 2 floppy drives and Microsoft Fortran 3.3.1- I could make a cup of tea - much more civilised.
JMN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
John Nichols wrote:To use an agricultural analogy, you have to plant the seed in order to have a tree from which you can shake down the fruits.
So PARDISO is a looped program, one can use it multiple times - hence the term phase, interesting turn of phrase.
I have been playing with some water supply analysis codeIf this is about flowing liquids in a pipe network, the equations would be nonlinear (loop flows or node pressures being the unknowns). The connectivity would be such that the equations are sparse but probably not narrowly banded.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Yes, it is about liquids flowing.
There are two methods to solve this problem - the first is to use the Hardy Cross method, which is actually quite efficient but you have to develop code to create the closed loops in your network. Not hard, just a pain. Streeter and Wylie in the 1960's and 70's in their classic textbook - Fluid Mechanics provided a Basic program that did the Hardy Cross. I was doing some water supply analysis with 2000 node networks in the late 1980's and used an Australian program called WATSYS to complete the analysis. You had to drive to Sydney, (3 hours) pay for parking ($50) and then do the run on a mainframe ($200) so I wrote my own code in Fortran to do the Hardy Cross based on the Basic program, and developed it over the years. I used AutoLISP to create the large scaled networks and layers to code the data. I had to export the data each time I did anything. Painful and you need to format the data correctly.
Then I went into PhD land and forgot about it.
Now, in the late 1980's a couple of bright profs invented the gradient method, i.e. set the flows to some low value, calculate the heads and then iterate, but you are doing a stack of inversions. Rossman from the EPA wrote the standard code that everyone uses - EPANET. It is in C last compiled using the VS 6 C compiler. The interface is in Pascal. The current VS 2013 compiler goes into meltdown land with the C code.
Elad published the very first iteration of EPANET from 1991. It was only 1400 lines of C code, so I looked at it and at exactly the same time a group asked for some help with infrastructure, so I got interested. The alternative is to write a program to translate the data from AutoCAD each time, that is painful.
I had the choice of Fortran or C# and so to practice my C# and to run it inside AutoCAD I translated the C code into C#, I also got DEV-CPP, an old one, to compile the C code so I could compare the answers. It took two weekends of fun to sort out the code and solve the problems. I was using some elements of the Streeter code, as they have some nice ideas.
Rossman's original code used a very old equation for the flows in the pipe, so I am now modifying it to include the Darcy Weisbach equation. I had problems with all of the pump curve equations that had been used in all of the programs - so whilst swimming with my 7 year old daughter I figured out a transformation onto the 0,0 to 1,1 plane and inversion to provide a simple cubic method for solving the problem. Much simpler and gave better answers than the older methods.
Once I had the C# code running I started to look at bigger models - actually ones created just as test cases. Then I had a nice computer crash and corrupted the registry - I thought I had copied off all of the code, but I left off a copy of the C# code, all I had was a printout of the C# code. So I scanned and entered the almost complete code and then spent an enjoyable weekend fixing it. (It got a lot better). That way you really get to play with it.
The sample problem I was using took 70 iterations to solve using the Rossman method, so I had a little play with the algorithm and got it to converge in 15. If each iteration takes 20 minutes that is a big saving.
You can renumber the nodes internally to create a fairly tight banded matrix, the structures people do this.
I then went and looked at the EPANET current code and you can see the old code embedded in the new. The sparse solver in the code comes from a 1981 paper. The main difference between the 1991 and 2008 code is error checking, not a big deal for someone who is only playing.
So once I had the algorithm correct and had some sample problems with answers, I started to look at the solver. I found MathNet Solver and tried that - really to get rid of the Rossman solver. It works but it is slow - very slow. MathNet has a method for using the MKL library and I tried that but it did not work with the current MKL and so I decided to ask the MKL experts.
PARDISO appears to be an excellent solution. It should not be that hard to call from C# and hopefully run directly on the data in AUTOCAD.
As usual the Intel forums have the people with all of the answers.
The rather interesting problem is that the model I used for the testing has a known solution - I used symmetry and a few other tricks to make it easy to solve by hand, but large enough to be a test. Rossman's algorithm has some minor errors that I cannot find. I get the right answers with the C# code, which is conceptually the same, but not Rossman's.
A lot of people use the EPANET program, it is available and people modify it and sell it commercially, and I am really interested in research aspects - not commercial aspects. I am not going to make a big model for a city again.
So now to integrate the PARDISO routine into the C# program and try to get directly at the AutoCAD data. (Fun really).
A group of my students have been looking at the movement of fungi spores from construction zones around hospitals into the hospital wards, quite a few people die from the spore infections in hospital each year. We built a simple device to mimic the air movement. I am thinking we can do a full analysis of a hospital room tracking every atom etc in the air and see if we can stop the fungi landing on the patients. Our computer people think it will be a bit hard for us - I think not.
Thanks for your help
JMN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Out of curiosity (I had written programs to do just this kind of calculation decades ago), I downloaded the source code of the DLL from http://www.epa.gov/nrmrl/wswrd/dw/epanet.html#downloads, and compiled the DLL using the current version of Visual C. The DLL got built with no errors, once I noted a couple of conventions: 1) everything is 32-bit; 2) because the DLL is to be called from Delphi/VB/..., the binary interface is STDCALL. So, here is how to build the DLL after unzipping the source files.
In the directory where I unzipped epanet2.zip, I used the command:
cl /Ot /LD /I. /Gz *.c /Feepanet2.dll epanet2.def
Similarly, I built the command line analyzer using
cl /Ot /I. /MD /DCLE *.c /Feepanet2.exe
and was able to run the example problem in the manual with the resulting EXE.
I don't know which version of the EPANET source you tried that gave you problems when compiling using VC.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Yes you are right - that worked.
I tried inside the VS IDE.
JMN
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
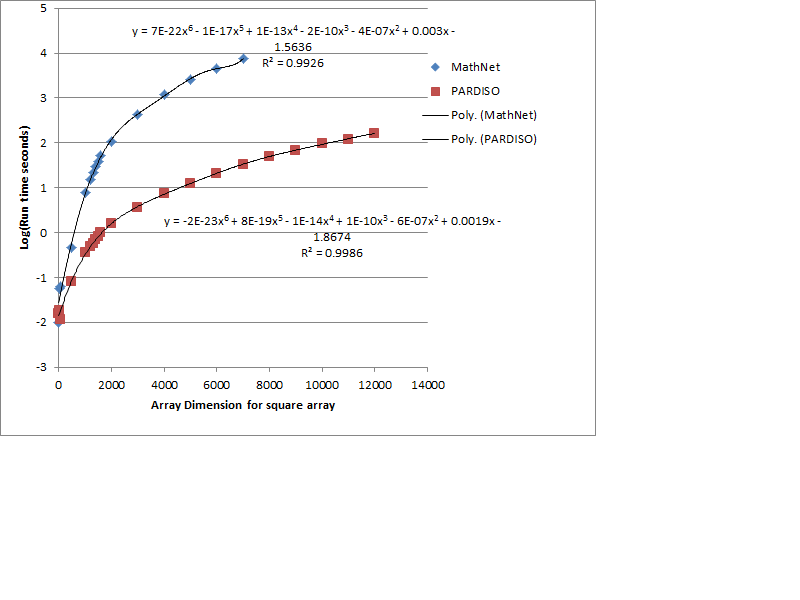
I have the PARDISO running quite nicely with quite large arrays - much larger than anyone would ever need.
Just to make sure it was worth while I tested the PARDISO against MathNet inversion routine. It was a lot better result than I ever thought it would be. The test used dense (matrices with zero - zero entries.) The EXCEL plot shows the results - which will be part of a future paper on water supply modelling. The limits are imposed by
1. for MATHNET - time - I was not prepared to wait 8 hours for one inversion to prove it was 8 hours.
2. The PARDISO runs into a problem with arrays bigger than 12,500 by 12,500 that are dense. Program gets to large to run in Windows. I assume if I use allocate I can break this boundary.
All of the links to the samples calling PARDISO from C# on the Intel web site are broken. Can I get a sample please?
I was actually hoping to put the PARDISO into a DLL (Intel Fortran) and call it from the C# code.
I got the Fortran running but it will not load as soon as it calls PARDISO.
Thanks
JMN
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page