UPDATE: PARDISO memory consumption for unsymmetric complex problem

FranciscoOrlandini · ‎12-20-2022

Hello,

Since I am unable to comment/reply/edit my previous post, I am starting a duplicate with updated info at the bottom of the post. I am sorry, but I couldn't think of any other alternative.

ORIGINAL POST:

I am trying to use PARDISO for solving a structurally symmetric complex matrix generated by a FEM scheme, and I am quite confused by its memory requirements.

When running PARDISO with a 144k equations matrix, I see a memory consumption up to 3GB in the factorization step. If I disable the permutation, by setting perm[i]=i in the perm array and iparm[4] = 1, it goes up to 5GB (I will use C++ 0-based indexing in this post as to avoid confusion).

I find this behavior to be a bit surprising, given that for symmetric real problems I normally see a negligible memory consumption for matrices around the same size.

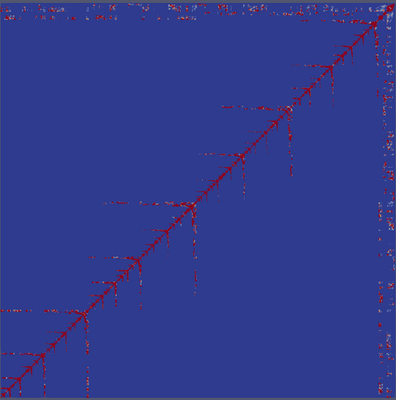
Attached you can see the sparsity pattern of the input matrix

with the red color denoting non-zero positions (each block actually corresponds to ~15 equations).

With iparm[4] = 2 I was able to inspect the matrix after PARDISO's reordering, and its sparsity pattern is as follows

Is this memory consumption considered normal? This matrix is obtained from a really coarse mesh, so for any practical application I wouldn't be able to use PARDISO if that is the case (perhaps with OOC mode, with I wouldn't expected to be needed for systems this big).

I first had this results using 32bit interface of oneAPI MKL 2021, and I didn't get any different results by using the 64bit interface of both 2021 and 2023 MKLs. All the tests were performed in a C++ code compiled with gcc in a Linux environment.

Unfortunately I cannot post here an easy way to generate such results, as it would require to download and compile a C++ library.

If there is further information that I could provide in order to provide more insight to this problem, I would be really happy to do so.

Thank you in advance.

UPDATE:

I have managed to isolate the problem in a single .cpp file and three text files containing the matrix in the CSR format.

The files can be obtained in this Google Drive link , and below one can see PARDISO's output.

Best regards,

Francisco

=== PARDISO is running in In-Core mode, because iparam(60)=0 ===

Percentage of computed non-zeros for LL^T factorization
 1 %  2 %  3 %  4 %  5 %  6 %  7 %  8 %  9 %  10 %  11 %  12 %  13 %  14 %  15 %  16 %  17 %  18 %  19 %  20 %  21 %  22 %  23 %  24 %  25 %  26 %  27 %  28 %  29 %  30 %  31 %  32 %  33 %  34 %  35 %  36 %  37 %  38 %  39 %  40 %  41 %  42 %  43 %  44 %  45 %  47 %  48 %  49 %  51 %  52 %  53 %  54 %  55 %  56 %  57 %  58 %  59 %  61 %  62 %  63 %  64 %  65 %  67 %  69 %  71 %  73 %  75 %  77 %  78 %  79 %  80 %  81 %  82 %  85 %  88 %  90 %  92 %  93 %  95 %  96 %  97 %  98 %  99 %  100 % 

=== PARDISO: solving a complex structurally symmetric system ===
Matrix checker is turned ON
0-based array is turned ON
PARDISO double precision computation is turned ON
METIS algorithm at reorder step is turned ON
Single-level factorization algorithm is turned ON


Summary: ( starting phase is reordering, ending phase is factorization )
================

Times:
======
Time spent in calculations of symmetric matrix portrait (fulladj): 0.038899 s
Time spent in reordering of the initial matrix (reorder)         : 0.719669 s
Time spent in symbolic factorization (symbfct)                   : 0.164026 s
Time spent in data preparations for factorization (parlist)      : 0.004884 s
Time spent in copying matrix to internal data structure (A to LU): 0.000000 s
Time spent in factorization step (numfct)                        : 15.284947 s
Time spent in allocation of internal data structures (malloc)    : 0.024751 s
Time spent in additional calculations                            : 0.305008 s
Total time spent                                                 : 16.542184 s

Statistics:
===========
Parallel Direct Factorization is running on 6 OpenMP

< Linear system Ax = b >
             number of equations:           144657
             number of non-zeros in A:      8811657
             number of non-zeros in A (%): 0.042109

             number of right-hand sides:    1

< Factors L and U >
             number of columns for each panel: 72
             number of independent subgraphs:  0
< Preprocessing with state of the art partitioning metis>
             number of supernodes:                    16666
             size of largest supernode:               4251
             number of non-zeros in L:                77945805
             number of non-zeros in U:                73504188
             number of non-zeros in L+U:              151449993
             gflop   for the numerical factorization: 1100.816559

             gflop/s for the numerical factorization: 72.019651