- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I aim to implement a lower latency version of jacobi 2d stencil. The default version is depicted below in the code snippet:
for(auto i = 1; i < N - 1; ++i) {
for(auto j = 1; j < N - 1; ++j) {
*B[i][j] = 0.2 * (*A[i][j] + *A[i][j-1] + *A[i][1+j] + *A[1+i][j] + *A[i-1][j]);
}
}
for(auto i = 1; i < N - 1; ++i) {
for(auto j = 1; j < N - 1; ++j) {
*A[i][j] = 0.2 * (*B[i][j] + *B[i][j-1] + *B[i][1+j] + *B[1+i][j] + *B[i-1][j]);
}
}
Note that there are 2 matrices, and their values are updated one after the other with respect to each other's values. The stencil basically calculates the average of north, south, east, west cell values of the cell and the cell's value itself.
Suppose that values in the matrix are "double" and matrix is represented with double A[N][N], N being the number of items in a single row/column.
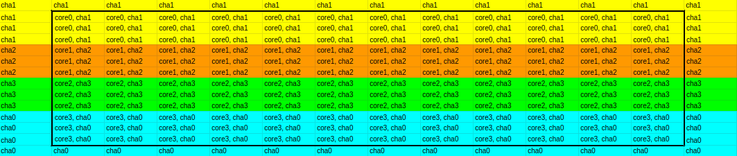
Instead of the conventional way of using 2d double array to create the matrix, I opted for a 2d matrix that consists of pointers to doubles (double* A[N][N]). Let's call this "cha-aware matrix". The reason I have done it this way is that I will parallelize the code such that each core that a thread is bound to will be co-located with the CHA that manages coherency of the memory addresses that respective thread is modifying/reading. For the sake of argument, assume that my system has 4 cores, and core-cha mapping is as follows: core0-cha1, core1-cha2, core2-cha3, core3-cha0. Here is the matrix I would construct for this system for N=14:
This matrix represent both A and B matrices. Here, note that the outermost cells are actually "ghost cells", and no thread are going to update values on those cells, that is why there are no core numbers assigned for those. In the image, "core x" actually means "thread bound to core x", so cores here represent threads. In addition to that, as it can be inferred from the image, I aimed to distribute the load among the cores as much as I can.
I am aware of the fact that I am sacrificing cache locality by creating a customized matrix this way and microbenchmark results showed that my version is actually a lot slower probably due to this reason. Creating an optimized coherence traffic across the mesh probably does not compensate for the slow down we are getting from non-contiguous memory accesses and I can understand that. Here is my actual code, I used OpenMP for parallelism.
#pragma omp parallel num_threads(18)
{
stick_this_thread_to_core(cores[omp_get_thread_num()]);
for(int t = 0; t < T; ++t) {
#pragma omp for collapse(2) schedule(static)
for(auto i = 1; i < N - 1; ++i) {
for(auto j = 1; j < N - 1; ++j) {
*B[i][j] = 0.2 * (*A[i][j] + *A[i][j-1] + *A[i][1+j] + *A[1+i][j] + *A[i-1][j]);
}
}
#pragma omp for collapse(2) schedule(static)
for(auto i = 1; i < N - 1; ++i) {
for(auto j = 1; j < N - 1; ++j) {
*A[i][j] = 0.2 * (*B[i][j] + *B[i][j-1] + *B[i][1+j] + *B[1+i][j] + *B[i-1][j]);
}
}
}
}
By checking from top command and pressing 1, I can see that bind is successful and cores all get busy.
However, here is the weird part: Instead of a constructing the matrix like I did above, I am creating a totally random matrix (in the form of double* A[N][N] again), in which assigned CHAs of the memory addresses in the contiguous cache lines that I am placing into the matrix are not the same (Sidenote: Coherency of memory addresses residing in the same cache line will always be managed by the same CHA). So, this way what I think is that I am not only sacrificing cache locality, but also messing up with the coherence traffic across the mesh. I was expecting that employing jacobi 2d stencil on this matrix would yield the worst results, but this was not always the case. Assuming that step count (T) is 20'000, and N is 1000, this "random matrix" results in a better latency than "cha-aware matrix", and I just cannot make sense of this result. On the other hand, when T is the same and N is 500, "cha-aware matrix" yields better results than "random matrix". When N is 50, again, "random matrix" is better. What are the possible factors that made it possible for this "random matrix" perform better in some cases?
Server I am running the microbenchmark on is Skylake Intel(R) Xeon(R) Gold 6154 with 18 cores enabled. It has just 1 socket. Turbo-boost is enabled on the server and there are 16 isolated cores, that implies OS can only use 2 of them for scheduling purposes. I am compiling with g++ with no optimizations and -march=native and -fopenmp flag.
I am sure that CHA-address mapping is correct, since I have implemented a way to figure out mapping with 2 vastly different methods, and they both spit the same mapping.
Would linux perf tool be beneficial for pinpointing what is really going under the hood?
Hope I was clear about explaining the problem, best regards.
@McCalpinJohn I wonder if you have any insights into this?
Same question on SO: https://stackoverflow.com/questions/71580417/confusing-results-on-cha-aware-jacobi-2d-microbenchmark
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The analysis here is not easy even for the single-thread case.
When I was doing related experiments with memory mapped to the co-located L3 slice, I had to be very careful to ensure that the *lists* of addresses that mapped to the local L3 were small enough to be held in the local L1D+L2 caches. In your implementation the locality information is stored in the extra pointers used for indirection. Since that extra storage will not be "locality-aware", it also needs to be small enough to be L1+L2-cacheable or else it will create unwanted cross-chip read traffic.
It is also important to disable the HW prefetchers when running this sort of code -- they will very aggressive fetch consecutive addresses, which will always be mapped to non-local L3 cache slices.
Once these two issues are addressed, the OpenMP version can be built. It is best to stay away from the OpenMP data parallel model where OpenMP distributes arbitrarily-sized loops over a fixed set of threads. Instead, create a simple OpenMP parallel loop where the loop index is the thread number, then each iteration of the loop will be a thread running an independent copy of the single-thread code optimized for L3 locality. The other advantage of this approach is that it is easy to instrument the code so that you can measure the execution time of each thread independently -- looking for variations in thread start time, thread execution duration, and thread post-execution barrier waiting time. I use RDTSCP in the "master" thread before and after the OpenMP Parallel For construct -- in Intel processors the TSC is tightly synchronized within a single socket, so you can compare TSC times across cores accurately. This approach will enable you to find cases for which the overall performance is degraded by a subset of the threads -- a common characteristic of performance problems due to cache conflicts or memory contention....
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page