- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
| Stride | Read count | Write count |
| 1 | 13,171,678.20 | 6,832,089.20 |
| 8 | 13,092,354.44 | 6,750,445.80 |
| 20 | 13,040,420.45 | 6,745,406.20 |
| 40 | 11,854,984.17 | 6,713,341.40 |
| 60 | 8,645,749.53 | 6,657,180.20 |
| 100 | 2,390,520.03 | 6,511,863.80 |
| 200 | 1,373,017.14 | 6,442,882.00 |
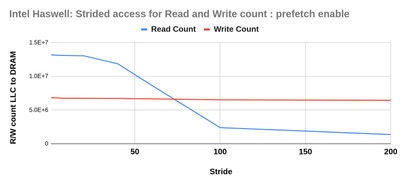
We observed the read counts are reducing with a higher number of strides (as expected). But the write counts are not decreasing at the same rate and the change is very little. We also tried disabling hardware prefetch but that also did not impact the write count.
Is it because of the periodic flush of the write combining buffer?
or why the write count will be like this?
Please help me to understand.
Thanks.
Monil
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
It seems to me that the c array is allocated and initialized by the kernel on the first write to 4KB page of the array (I'm assuming it's allocated as 4KB pages larger than large pages). When a 4KB page is initialized, all lines become dirty irrespective of how many write you're actually doing on the page. You can check, for example, whether the number of DRAM writes is halved for a stride that is big enough to only write to alternate pages (2048 for 4KB pages).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi, you are absolutely right. Thanks a lot.
4KB page size was not giving me the result. So I kept increasing the stride size and found that the page size it is considering is 2MB (I found this is also a huge page size for intel). If I make the stride bigger than that, then the write count becomes half.
I have one question though:
C array was not initialized, that is why it is happening. My question is why all lines become dirty for this scenario? It is causing extra unnecessary data transfer from the memory controller( since I am counting from the uncore memory controller counters) to DRAM. It seems inefficient. It would be great if you discuss it a little bit.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
When pages are first mapped to any user process, care must be taken to avoid information leakage from the previous contents. This is almost always accomplished by zeroing the pages.
There are a couple of different places where it might make sense to zero the pages. They could be zeroed before they are returned to a free page list, or they could be zeroed when they are instantiated/mapped.
The zeroing of the page can be done explicitly (e.g., executing memset()), or can be done implicitly by mapping the page to the "zero-page", with copy-on-write enabled. There is a fair amount of OS overhead involved in the manipulation of the free page tables and user page tables, making it difficult to understand what is happening from performance counter data alone.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the explanation.
So far I found there are four page sizes. The default one is 4KB and then there are huge page size of 2MB, 4MB or 1GB.
In this particular example, page size 2MB was used. How does the os decide when to use which page size?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
When running in 64-bit mode (any modern operating system), Intel processors support 4KiB, 2MiB, and 1 GiB pages. The 4MiB page size is only supported in a 32-bit legacy operating mode that I have not seen in a long time....
Linux uses 4KiB pages by default. Most versions of Linux support a mechanism called "Transparent Huge Pages", which invisibly maps user data (stack and heap) on 2MiB pages if the OS is able to create enough 2MiB pages -- when the OS is unable to provide 2MiB pages for all or part of an allocation, 4KiB pages are used. Transparent Huge Pages may be enabled by default on your system.
Linux also supports explicitly reserved 2MiB and 1GiB pages. To use these reserved pages, you need to make a special request with the memory allocation -- I usually use "mmap()" with the options "MAP_HUGETLB | MAPHUGE_2MB" or 2MiB pages or "MAP_HUGETLB | MAPHUGE_1GB" for 1GiB pages.). You can attempt to reserve large pages on a running system, but there are no guarantees of success. (If the system is idle, you may be able to get a lot of 2MiB pages -- maybe 1/4 or more of the total memory. Lots of my systems can't allocate any 1GiB pages even when idle if they have been up and running for more than a day or two.) Large pages can be reserved at boot time much more reliably, but then another reboot is required to release them.
Transparent Huge Pages are massively more useful, but it requires extra work to ensure that your allocations have actually been made on large pages if you are doing carefully controlled benchmarks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks a lot for the nice explanation.
For a case, C = A + B where A and B are initialized. C is not initialized. 100M data size.
Now I understand the reasoning for the write traffic since it halves after 2MB stride (524288).
However, for read traffic, I am also noticing something peculiar. after stride 128 to 2MB stride (red marked) the traffic does not halve even though the stride is doubled. It seems the read traffic in this case also has a relationship with page size since this behavior continues till 2MB stride. But A and B are initialized. I tested it in Broadwell, Sky Lake, and Cascade Lake. Same behavior everywhere. However, if we initialize C array, then the read traffic halves with stride doubling and do not show this kind of plateauing. Also, it is not related to prefetching. I disabled prefetching and the same result is found. It would be great if you could shed some light on this.
| Stride | Read traffic | Read ratio | Write traffic | Write ratio |
| 1 | 13159180 | 6932222 | ||
| 2 | 13034186 | 1.01 | 6871207 | 1.01 |
| 4 | 12938265 | 1.01 | 6798102 | 1.01 |
| 8 | 12891037 | 1.00 | 6758055 | 1.01 |
| 16 | 12906523 | 1.00 | 6774366 | 1.00 |
| 32 | 6616530 | 1.95 | 6535310 | 1.04 |
| 64 | 3468820 | 1.91 | 6462811 | 1.01 |
| 128 | 1907931 |
1.82 |
6406911 | 1.01 |
| 256 | 1120988 | 1.70 | 6386789 | 1.00 |
| 512 | 722937 | 1.55 | 6361076 | 1.00 |
| 1024 | 528230 | 1.37 | 6331793 | 1.00 |
| 2048 | 430157 | 1.23 | 6328232 | 1.00 |
| 4096 | 376966 | 1.14 | 6321227 | 1.00 |
| 8192 | 364022 | 1.04 | 6347827 | 1.00 |
| 16384 | 345926 | 1.05 | 6346390 | 1.00 |
| 32768 | 337696 | 1.02 | 6337854 | 1.00 |
| 65536 | 334612 | 1.01 | 6343776 | 1.00 |
| 131072 | 332902 | 1.01 | 6344102 | 1.00 |
| 262144 | 334644 | 0.99 | 6344325 | 1.00 |
| 524288 | 329619 | 1.02 | 6308766 | 1.01 |
| 1048576 | 170707 | 1.93 | 3163299 | 1.99 |
| 2097152 | 81720 | 2.09 | 1534614 | 2.06 |
| 4194304 | 39529 | 2.07 | 736773 | 2.08 |
| 8388608 | 18746 | 2.11 | 357127 | 2.06 |
| 16777216 | 8556 | 2.19 | 162377 | 2.20 |
| 33554432 | 3492 | 2.45 | 63110 | 2.57 |
| 67108864 | 1773 | 1.97 | 24575 | 2.57 |
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There is a lot of "stuff" going on here, and it is not clear what experimental conditions the most recent table applies to. The text says that "if we initialize C array, then....", but the table shows writes consistent with C being instantiated at a 2MiB page size. If C is being instantiated, then the corresponding OS code will generate additional read traffic (and perhaps some additional write traffic), making everything very hard to understand.
Recommendation -- if you want to understand what is happening with array instantiation, do not combine the measurements with other unrelated activity. Focus on exactly one thing at a time, control it as well as possible, and don't move to combined operations until you have an adequate understanding of each of the components in isolation. Here you are trying to understand the interaction of many, many mechanisms all jumbled together:
- Page Instantiation by the OS -- including all the extra cruft from Transparent Huge Pages
- Demand Reads with strides
- Demand Writes with strides
- Hardware Prefetching on a combination of strided reads and strided writes, with:
- 2 L1 HW Prefetchers (IP and streaming) -- with different behaviors for reads and writes
- 2 L2 HW Prefetchers (adjacent line and streaming) -- with different behaviors for reads and writes
- Next-Page Prefetcher (cannot be disabled)
Trying to understand the details of these complex, combined tests is unlikely to be helpful until the components are understood in isolation.
You might be surprised that this is not well understood, but outside of the Intel design team, the operation of the hardware prefetchers on *contiguous* data is still an active topic of research. The prefetchers' basic algorithms are only described by Intel at a high level, and the prefetching behavior changes dynamically over very short times scales (too short to measure) depending on some (effectively undocumented) measure of how "busy" the cache is, and/or how many outstanding misses that level of cache is already tracking.
The L2 HW PF behavior has changed significantly with the introduction of the non-inclusive L3 cache in Skylake Xeon and Cascade Lake Xeon. In addition, the "memory directory" feature is enabled by default in 2-socket Skylake Xeon and Cascade Lake Xeon processors, which can significantly bias results if there are any remote DRAM accesses. (This feature is not enabled by default on 2s Xeon E5 v3 (Haswell EP), but I have not checked whether it is enabled by default on 2s Xeon E5 v4 (Broadwell EP).)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Describe your experiment precisely! Show the whole code, including the code that allocates and initializes the arrays. Specify which part of the code is being measured and how (which tool?). Specify the compiler version and switches and the kernel version. Also it's not clear to me what you meant by "100M data size." Do you mean that the size of an array is 100 million 4-byte elements? Or maybe 100 million bytes? Or 100 million MBs? All of these details (and others) are important.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
@McCalpinJohn: thanks again. I learn something new every time you respond.
I understand I was not very clear while asking the question. Let me present it again.
1. Prefetching is disabled. (all four bits in MSR 0x1A4).
2. code is given at. https://github.com/monil01/memory_research_ornl/blob/master/vecmul_cpu/vecmul.c
This code is for vector multiplication. Two arrays h_a and h_b are initialized with some value. Array h_c is just allocated. The multiplied result is stored in h_c.
4. processor: Xeon E5-2683 v4 processor of the Broadwell family.
5. Uncore IMC counters are used. bdx_unc_imc[0|1|4|5]::UNC_M_
6. PAPI native counters and TAU with PAPI native counter support is used to generate data for the vecMul() function. So the reported data is only for vector multiplication which excludes all other functions in the code.
7. The data size of each array: 100M floating points. Stride is given in the table.
With this setting, we got the following data.
| Stride | Read | Read ratio | Write | Write ratio |
| 1 | 13159180 | 6932222 | ||
| 2 | 13034186 | 1.01 | 6871207 | 1.01 |
| 4 | 12938265 | 1.01 | 6798102 | 1.01 |
| 8 | 12891037 | 1.00 | 6758055 | 1.01 |
| 16 | 12906523 | 1.00 | 6774366 | 1.00 |
| 32 | 6616530 | 1.95 | 6535310 | 1.04 |
| 64 | 3468820 | 1.91 | 6462811 | 1.01 |
| 128 | 1907931 | 1.82 | 6406911 | 1.01 |
| 256 | 1120988 | 1.70 | 6386789 | 1.00 |
| 512 | 722937 | 1.55 | 6361076 | 1.00 |
| 1024 | 528230 | 1.37 | 6331793 | 1.00 |
| 2048 | 430157 | 1.23 | 6328232 | 1.00 |
| 4096 | 376966 | 1.14 | 6321227 | 1.00 |
| 8192 | 364022 | 1.04 | 6347827 | 1.00 |
| 16384 | 345926 | 1.05 | 6346390 | 1.00 |
| 32768 | 337696 | 1.02 | 6337854 | 1.00 |
| 65536 | 334612 | 1.01 | 6343776 | 1.00 |
| 131072 | 332902 | 1.01 | 6344102 | 1.00 |
| 262144 | 334644 | 0.99 | 6344325 | 1.00 |
| 524288 | 329619 | 1.02 | 6308766 | 1.01 |
| 1048576 | 170707 | 1.93 | 3163299 | 1.99 |
| 2097152 | 81720 | 2.09 | 1534614 | 2.06 |
| 4194304 | 39529 | 2.07 | 736773 | 2.08 |
| 8388608 | 18746 | 2.11 | 357127 | 2.06 |
| 16777216 | 8556 | 2.19 | 162377 | 2.20 |
| 33554432 | 3492 | 2.45 | 63110 | 2.57 |
| 67108864 | 1773 | 1.97 | 24575 | 2.57 |
Here, the ratio is determined from two consecutive values to see if the ratio is close to two since the stride is doubled every time.
Now I understand the reasoning for the write traffic since it halves after 2MB stride (524288).
However, for read traffic, I am noticing something peculiar. after stride 128 to 2MB stride (red marked) the traffic does not halve even though the stride is doubled. It seems the read traffic in this case also has a relationship with page size since this behavior continues till 2MB stride.
For example with a stride of 8192, the total number of array access to a 100M long array is 12207 * 2. on the other hand, for a stride of size 262144, the total number actual array access is 381 * 2 times. But still, the read traffic suggests a similar number of cacheline transfers which are 364022 and 334644.
I am trying to understand this.
If you could also point me where to look at the documentation, it would be great.
Thanks,
Monil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
As I noted before, when your code includes the initial instantiation of the arrays, your measurements include the OS code for page instantiation. Unless you know that stack in detail (and I don't know anyone who does), you are not going to be able to understand what memory traffic is due to the page instantiation and what is due to the code that you wrote. You appear to be lucky in getting DRAM CAS WRITE results that are a fairly close match to what is required to write-back each 2MiB page, but that does not mean that the page instantiation code is not also generating CAS reads!
I am also not sure whether the code is doing what you expect for the largest strides. With an array size of 100M floats, the stride of 67,108,864 will only execute twice -- once for element 0 and once for element 67,108,864. The count of 1773 reads is more than a little bit high for 2 loads, and is likely dominated by some combination of the CAS READ traffic required to instantiate the 2 2MiB pages that are accessed and possibly the CAS read traffic required to read the performance counters.
It is important to keep track of the size of regions for which you are gathering performance counter data, so that you can compare those sizes with the overhead of reading the counters. For recent versions of Linux, PAPI uses the native "perf events" subsystem to collect performance counter data, and this requires a kernel entry and exit for each counter read. On my Xeon E5-2680 v4 system, the command "papi_cost" shows a minimum overhead of about 1500 cycles to read two core counters. This is for core counters, but the PCI configuration space counters used for the memory controller are not going to be any cheaper (see notes (1) & (2)).
For the current test, I recommend instantiating the output array separately from the strided access measurements, and adding an external repeat loop so that the number of user-space operations is closer to constant. Setting the repeat loop count to match the stride is a good option, or setting up an infinite loop with a break after a specified elapsed time is another commonly used approach.
Notes:
(1) I am not recommending this for your test, but these counters can be read directly from user space if you have root access and can mmap() the /dev/mem driver file. This reduces the overhead to two 32-bit uncached load instructions per counter, with typical latencies of ~250 cycles per load (depends a lot on the processor model). This approach makes sense when you really need to count DRAM accesses over a short time scale, or if you really need to count DRAM accesses with very low overhead -- e.g., https://github.com/jdmccalpin/periodic-performance-counters).
(2) The core counters can also be read directly from user space if the kernel is configured correctly and the MSRs have been configured correctly. This is also not really necessary for your test, but there is no harm in it, and it can reduce the overhead (in execution time, in instructions, and in the associated cache traffic) significantly. This approach requires that the thread run on the same logical processor for the duration of the test (because the hardware performance counters are not virtualized in this case). This approach is used by https://github.com/jdmccalpin/low-overhead-timers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The size of each array is 100,000,000*4/64 = 6,250,000 cache lines, each has a unique physical address assuming there is enough physical memory to hold all of them simultaneously, which is likely the case. In the case of accessing all elements, the vecMul function by itself should cause the following events:
- 6,250,000*2 = 12,500,000 memory reads for reading the elements of a and b. 6,250,000 memory writes for writing to array c. This is assuming the following: (1) the kernel initializes each page on the first access, (2) the size of all pages is 2 MB or 4 KB, (3) the kernel uses string store instructions to initialize pages. All of these assumptions appear to be held here, which is typical on a Linux kernel. Otherwise, the results would be very different.
With a stride of 1, the measured number of memory reads and writes is 13,159,180 and 6,932,222, respectively. Each is higher by about 670,000 than what the vecMul function should cause by itself.
As for the additional writes, the biggest reasons by far is the following. The a and b arrays are initialized just before vecMul. Therefore, even though the events are only measured for the vecMul function, there can be many dirty cache lines belonging to the last few pages of the a and b arrays that are still present in the cache hierarchy. The Xeon E5-2683 v4 has a 40 MB inclusive LLC, which can hold up to 655,360 dirty cache lines. These can result in up to 655,360 additional memory writes occurring during the execution of vecMul. Obviously, most of these additional writes can be eliminated by flushing the cache before calling vecMul.
As for the additional reads, there are multiple reasons listed in order of importance (roughly, according to my best guess):
- Access on the kernel page initialization path other than the particular code that does the actual initialization. This overhead is proportional to the number of accessed pages. Memory access from the MMU page walker. This overhead is proportional to the number of accessed pages. The initialization of the c array in the kernel may not leave all cache lines in the cache hierarchy before returning to vecMul. This may result in up to 6,250,000 additional reads. This overhead is proportional to the number of accessed cache lines and potentially other factors. In case the event are not filtered for the specific core on which the code is running, events from other cores may also be counted. This overhead is unpredictable on a busy system. Accesses from the measurement code. This overhead is fixed.
Overall, it's reasonable that the number of total memory reads measured is higher by about 660,000.
As the stride increases from 1 to 524,288, the distribution of accesses over the LLC cache sets becomes more biased, so the number of extra writes approaches zero (with stride 524,288, the number of writes is very close to 6,250,000). A detailed analysis is possible, if you care. The pattern of write counts for strides larger than 524,288 was already explained in my first post.
The gradual drop in the number of reads for strides 1 to 16 is not exactly clear to me. Perhaps it's in the range of run-to-run variation. Anyway, it probably has nothing to do with the vecMul function itself in isolation.
With data prefetchers turned off, starting with stride 32, the number of cache lines read from the a and b arrays is reduced by half. However, that doesn't mean that the total number of memory reads will also be reduced by half. For stride 16, the number of reads is 12,906,523, out of which 12,500,000 can be attributed to the reads from the a and b arrays. The number of additional reads is about 400,000. So for stride 32, the expected number of reads is no more than 6,250,000 + 400,000 = 6,850,000 and not less than 6,250,000. The measured number is 6,616,530, which is within the expected range. For strides 16 and 32, the number of additional reads comprises 3.1% and 5.5% of all reads, respectively. It's expected that the number of additional reads comprises an increasingly larger portion of all reads as the stride increases. Therefore, the reduction in the number of reads with increasingly larger strides becomes smaller and smaller, rather than halved each time. For stride 524,288, the vast majority of reads fall into the "additional reads" category and the reads from the arrays is equal to twice the number of (2 MB) pages accessed.
As discussed earlier, the number of additional reads is mostly proportional to the number of pages accessed, which appears to be is around 800-900 reads per accessed page, which is reasonable. Therefore, beyond stride 524,288, the number of accessed pages is reduced by half with increasing strides. Again, the vast majority of reads in this range of strides are additional reads and will be reduced in proportion to the reduction in the number of pages accessed. This explains the pattern of read count beyond stride 524,288.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I've posted an answer, but for some reason it's not appearing in this thread. Hopefully you got an email notification.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The size of each array is 100,000,000*4/64 = 6,250,000 cache lines, each has a unique physical address assuming there is enough physical memory to hold all of them simultaneously, which is likely the case. In the case of accessing all elements, the vecMul function by itself should cause the following events:
- 6,250,000*2 = 12,500,000 memory reads for reading the elements of a and b. 6,250,000 memory writes for writing to array c. This is assuming the following: (1) the kernel initializes each page on the first access, (2) the size of all pages is 2 MB or 4 KB, (3) the kernel uses string store instructions to initialize pages. All of these assumptions appear to be held here, which is typical on a Linux kernel. Otherwise, the results would be very different.
With a stride of 1, the measured number of memory reads and writes is 13,159,180 and 6,932,222, respectively. Each is higher by about 670,000 than what the vecMul function should cause by itself.
As for the additional writes, the biggest reasons by far is the following. The a and b arrays are initialized just before vecMul. Therefore, even though the events are only measured for the vecMul function, there can be many dirty cache lines belonging to the last few pages of the a and b arrays that are still present in the cache hierarchy. The Xeon E5-2683 v4 has a 40 MB inclusive LLC, which can hold up to 655,360 dirty cache lines. These can result in up to 655,360 additional memory writes occurring during the execution of vecMul. Obviously, most of these additional writes can be eliminated by flushing the cache before calling vecMul.
As for the additional reads, there are multiple reasons listed in order of importance (roughly, according to my best guess):
- Access on the kernel page initialization path other than the particular code that does the actual initialization. This overhead is proportional to the number of accessed pages. Memory access from the MMU page walker. This overhead is proportional to the number of accessed pages. The initialization of the c array in the kernel may not leave all cache lines in the cache hierarchy before returning to vecMul. This may result in up to 6,250,000 additional reads. This overhead is proportional to the number of accessed cache lines and potentially other factors. In case the event are not filtered for the specific core on which the code is running, events from other cores may also be counted. This overhead is unpredictable on a busy system. Accesses from the measurement code. This overhead is fixed.
Overall, it's reasonable that the number of total memory reads measured is higher by about 660,000.
As the stride increases from 1 to 524,288, the distribution of accesses over the LLC cache sets becomes more biased, so the number of extra writes approaches zero (with stride 524,288, the number of writes is very close to 6,250,000). A detailed analysis is possible, if you care. The pattern of write counts for strides larger than 524,288 was already explained in my first post.
The gradual drop in the number of reads for strides 1 to 16 is not exactly clear to me. Perhaps it's in the range of run-to-run variation. Anyway, it probably has nothing to do with the vecMul function itself in isolation.
With data prefetchers turned off, starting with stride 32, the number of cache lines read from the a and b arrays is reduced by half. However, that doesn't mean that the total number of memory reads will also be reduced by half. For stride 16, the number of reads is 12,906,523, out of which 12,500,000 can be attributed to the reads from the a and b arrays. The number of additional reads is about 400,000. So for stride 32, the expected number of reads is no more than 6,250,000 + 400,000 = 6,850,000 and not less than 6,250,000. The measured number is 6,616,530, which is within the expected range. For strides 16 and 32, the number of additional reads comprises 3.1% and 5.5%, respectively, of all reads. It's expected that the number of additional reads comprises an increasingly larger portion of all reads as the stride increases. Therefore, the reduction in the number of reads with increasingly larger strides becomes smaller and smaller, rather than halved each time. For stride 524,288, the vast majority of reads fall into the "additional reads" category and the reads from the arrays is equal to twice the number of (2 MB) pages accessed.
As discussed earlier, the number of additional reads is mostly proportional to the number of pages accessed, which appears to be is around 800-900 reads per accessed page, which is reasonable. Therefore, beyond stride 524,288, the number of accessed pages is reduced by half with increasing strides. Again, the vast majority of reads in this range of strides are additional reads and will be reduced in proportion to the reduction in the number of pages accessed. This explains the pattern of read count beyond stride 524,288.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page