How to configure DSP block in "three 9x9 multipliers" mode?

[shvlad]

Hi everyone

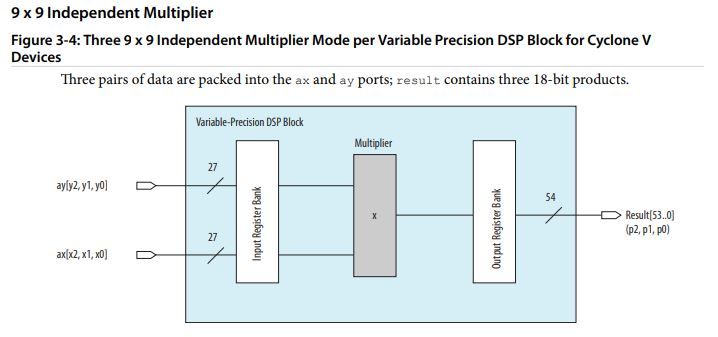
Please help me configure DSP block in "three 9x9 multipliers" mode. I have a Cyclone V family chip, I've read this document https://www.intel.com/content/dam/www/programmable/us/en/pdfs/literature/hb/cyclone-v/cv_5v2.pdf, there is picture and some description on page 3-11 about 9x9 mode. 

parameter W = 9   logic[W-1:0] data_0; logic[W-1:0] data_1;   logic[W-1:0] data_2; logic[W-1:0] data_3; logic[W-1:0] data_4; logic[W-1:0] data_5;   logic[W*2-1:0] m_0,m_1,m_2;

I've tried this ways:

1.

assign {m_0,m_1,m_2} = {data_0,data_1,data_2}*{data_3,data_4,data_5};

It makes one DSP, but output incorrect (It multiples one 27 bits figure not three 9-bits).

2.

assign {m_0,m_1,m_2} = {data_0*data_1,data_2*data_3,data_4*data_5};

It makes correct output, but takes three DSP.

And other ways fails too... For example

assign m_0 = data_0*data_1; assign m_1 = data_2*data_3; assign m_2 = data_4*data_5;

I've tried take mult IP from IP catalog, but it doesn't work too.

Please, tell me, how can I place three mult in one DSP?

[CheePin_C_Intel]

Hi, I would like to apologize for the delay in response. It seems like I encounter some issues with notification reaching my mailbox. Sorry for the inconvenience. As I understand it, you have some inquiries related to fitting 3 9x9 multipliers into a single DSP block in CV devices. As we understand it from the handbook seems like this is something feasible. I understand that you mentioned that when using mult IP it seems like not working as well. Mind further elaborate on the issue you encounter with the mult IP? Would you mind to share with me a simple test design of your using the mult IP so that I could have a better understanding of the configuration as well as to facilitate further debugging. Please let me know if there is any concern. Thank you. Best regards, Chee Pin

[shvlad]

Dear Mr. Pin

Thank you for your answer.

I've prepared a test project (archive was attached to this message). There are three ways to create a mult in this project. Please comment or uncomment "define" in line 2-5 and check them.

For ways 0 and 2 I have one DSP, but incorrect result, and correct result, but 3 DSPs for a way 1.

Please, give me an example where DSP block works in 3-mult mode. I've seen a lot of beautiful pictures, but I haven't seen any code examples.

[CheePin_C_Intel]

Hi, Thanks for sharing the QAR. Based on my understanding, the way 1 seems to be the right way for the implementation. I am able to replicate the observation of 3 DSP blocks being used in compilation. For your information, as I added logic lock region with only 1 DSP in the chip planner, and assign your design to it, the compilation is able to fit the three 9x9 multipliers into a single DSP block. For your information, generally if there are still sufficient DSP blocks in the device, the compilation will choose to utilize more DSP blocks for better timing and performance. Fitter will only try to pack into a single DSP block when there is limited DSP resources. Please let me know if there is any concern. Thank you. Best regards, Chee Pin

[shvlad]

Your answer is totally right!

I created this code

`timescale 1ns / 1ns   (* multstyle = "dsp" *) module mux_9x9 #( parameter L = 25 ) ( input logic [8:0] x_0[L], input logic [8:0] x_1[L], input logic [8:0] x_2[L],   input logic [8:0] y_0[L], input logic [8:0] y_1[L], input logic [8:0] y_2[L], output logic [17:0] p_0[L], output logic [17:0] p_1[L], output logic [17:0] p_2[L] );   genvar i; generate for( i = 0; i < L; i++ ) begin:MULT assign {p_0[i],p_1[i],p_2[i]} = {x_0[i]*y_0[i],x_1[i]*y_1[i],x_2[i]*y_2[i]}; end endgenerate endmodule

Quartus places three multi to one DSP when it doesn't have enough DSP (just change parameter "L").

[CheePin_C_Intel]

Hi, It seems like I am unable to attach the updated QAR to the Forum. I have sent it to you through email for your reference. Thank you.

[CheePin_C_Intel]

Hi, Thanks for your update. Glad to hear that hear that you have managed to verify the Fitter behavior. Please let me know if there is any concern. Thank you. Best regards, Chee Pin