- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
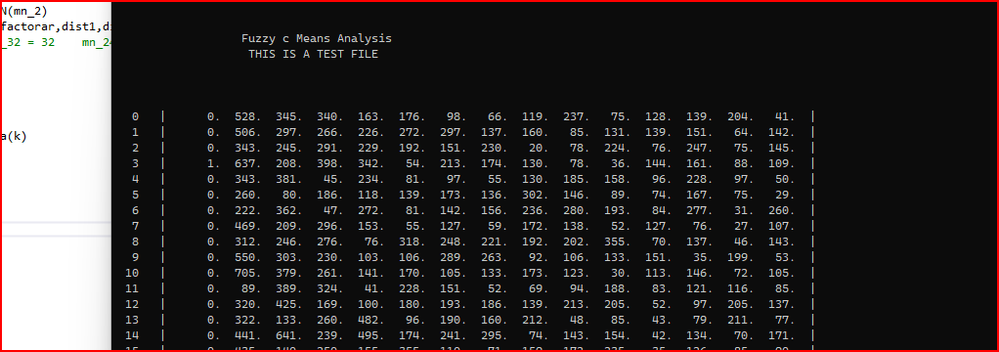
This morning I have been going back and slowly tidying up the output from the Fuzzy Means and Intel Fortran has been doing some interesting things.
WRITE(*,12738)NS, (Y(i,J),J=1,15) ! 00C85000
WRITE(sOUT,12738)NS, (Y(i,J),J=1,ND) ! 00C85000
12738 FORMAT(I4, 2x, " | ", 1(2X,15(F5.0,1X)), " | ") ! 00086000The last code gives green symbols on the VS cmd window - see picture. Does anyone know why this happens. The write statement is pretty stock standard.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
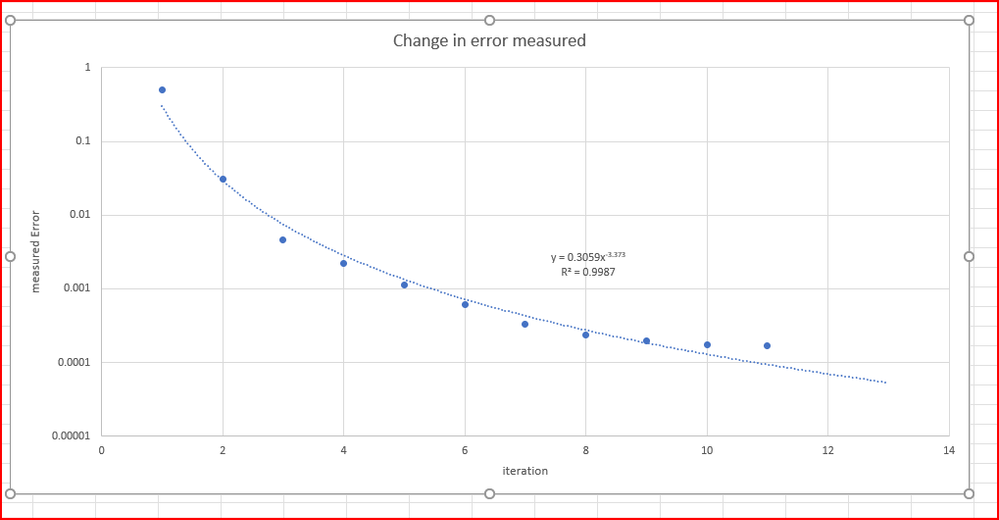
The second interesting element is the convergence on the error limit is following a power regression until it hits a limit of of about 0.00017, if I try and resolve at a lower limit, then the program just goes off in a slowly increasing harmonic cycle for the error. A slow harmonic rise. After about 34 iterations it is at about 0.00024 or thereabouts.
Any ideas, the limit is ok for what I want but it is interesting.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The program prints out the centers for each cluster vector. It provided a long list of i, j, value, which on an output window in pretty long. I have 510 input vectors each with 300 dimensions. I tried to change the output for the cmd window to 15 per line and only look at the first 15. I had a problem that each line of print gave me two sets of 30. See picture., for two clusters. The long printout is fine.
I then amended the code to just print one at a time and then hold the cursor on the line. I can do both by changing the value of trial.
DO 415 I=1,NCLUS
if(trial .eq. 0) then
write(*,4111)I
4111 format(/,20X,i3, 2x,\)
do j = 1, 15
WRITE(*,406) (V(I,J))
end do
else
WRITE(*,4071) (I,V(I,J),J=1,15)
end if
415 WRITE(sOUT,404) (I,J,V(I,J),J=1,NDIM)
404 FORMAT(20X, " I = ", I3,3X,"J = ",I3,3X,"V(I,J)= ",F8.4)
4071 FORMAT(20X, " I = ", I3,3X,15(F6.2,2X))
406 FORMAT(F6.1,2x,\)
405 FORMAT(1H ,7(F6.4,3X))Any ideas on what is my mistake? Line 9 give me the strange output. If I use line 6 no problems.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Finally, we have been discussing the topic of numbered do loops. I am slowly taking out the numbered do loops in this program, but the old problem of
do 100 I=1, NCLUS
DO 100 K=1,NSAMP
AU=U(I,K)
F(NCLUS)=F(NCLUS) +AU**2/ANSAMP
IF (AU) 100,100, 101
101 H(NCLUS)=H(NCLUS)-AU*LOG(AU)/ANSAMP
100 CONTINUEthis example needs two end do the compiler will not cope with one ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You might find it helpful to comment your continue statements as to how you get there. Then edit as necessary
100 CONTINUE ! do 100 I=..., do 100 K=...
Be careful to watch for DO and GOTO to the same CONTINUE. The two pass method will aid in eliminating coding errors (missing ENDIF or mission GOTO label).
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Shared DO loop continuation is a deleted feature, but as I have said before, compilers continue to support them. Many people didn't understand how they work - a branch to the shared CONTINUE is treated as a branch to the innermost loop's end.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
IIF this is an error value, the error value is made without stating what is the overall "part" size. IOW we would not know the precision of the error.
IIF this is an error ratio, then you would have to consider if the error calculation was derived from a linear, area, or volume measurement. (error, error**-2, error**-3)
If the error calculation is using sqrt or pow, then check to see which variation of the function is used.
In the case of sqrt, should the compiler optimized 1.0/sqrt(x) (and depending on CPU) this may result in 14 bits, 22/23 bits or 28 bits of precision. You can improve the accuracy with adding Newton-Raphson or Taylor series approximation following the initial approximation.
Jim Dempsey
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I stumbled across this Fuzzy c Means whilst I was looking at some K Means stuff. I am slowly unwinding the code and comparing the results to the K Means values. I had tried a commercial K Means formulation, but it does not allow you to stare into the working elements of the commercial function. The Fortran code allows one to play with the functions, without a lot of work and they are fast.
The code needs to be commented in greater detail, and the unwinding takes a while as I am looking at the results to see how they fit into the overall analysis.
The observation about the power function convergence did not occur until I pulled out the detailed printouts that just confused everything and got a decent picture. I was surprised by the result.
I will look at the Newton Raphson - but there is a ways to go yet.
I always thought the shared do loop was a kludge.
But for 700 lines of Fortran it does the trick.
The visual output is the key to understanding.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I was looking at NR technique, then I had a look at the data output for finding convergence. The suggested exponent for the least "squares" analysis from the authors is 1.2. Using this number and the Euclidian distance, the function never crosses zero on some of the 510 vectors. I moved up to 2 - standard least squares and it crossed zero in a few iterations and solved quite quickly.
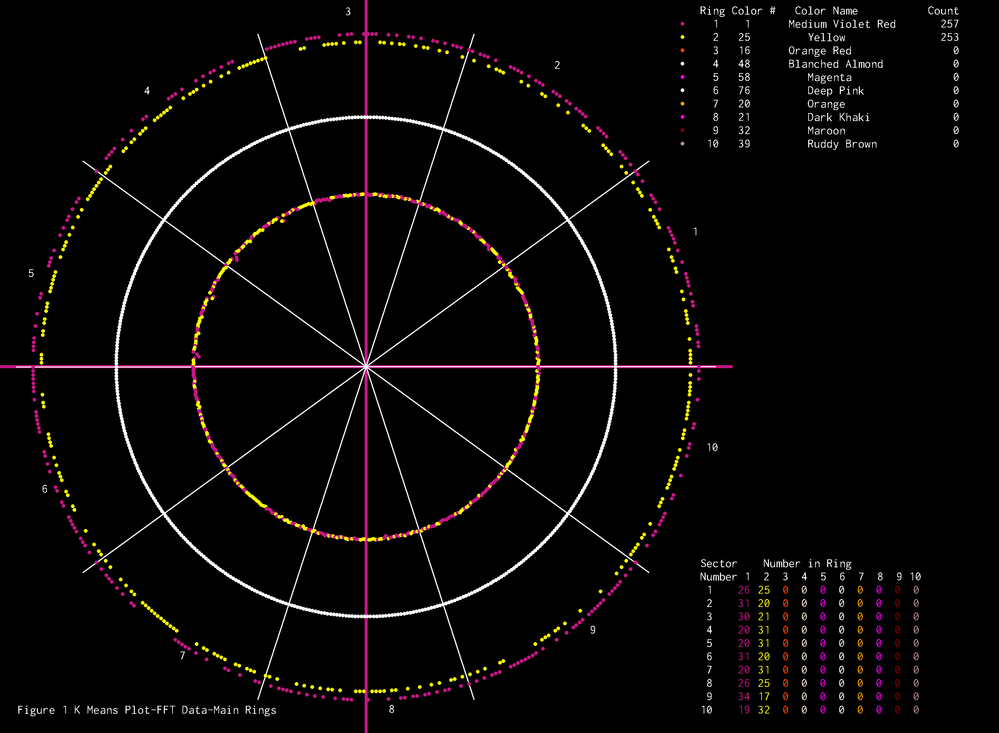
I also got the two other norms working, I need to add the parameter switch so I can see the parameters in the debug window. The is the result for exponent 2 and the Mahalanobis Norm. https://en.wikipedia.org/wiki/Mahalanobis_distance This is actually quite useful in signal analysis.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page