Fuzzy K means

[JohnNichols]

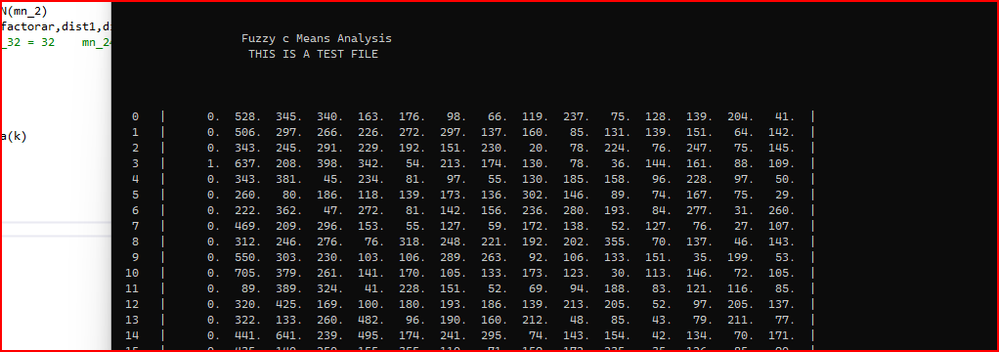
This morning I have been going back and slowly tidying up the output from the Fuzzy Means and Intel Fortran has been doing some interesting things.  

 WRITE(*,12738)NS, (Y(i,J),J=1,15)	                                                !   00C85000
        WRITE(sOUT,12738)NS, (Y(i,J),J=1,ND)	                                                !   00C85000
12738   FORMAT(I4, 2x, " | ", 1(2X,15(F5.0,1X)), " | ")	                                                !   00086000

The last code gives green symbols on the VS cmd window - see picture.  Does anyone know why this happens.  The write statement is pretty stock standard. 

[JohnNichols]

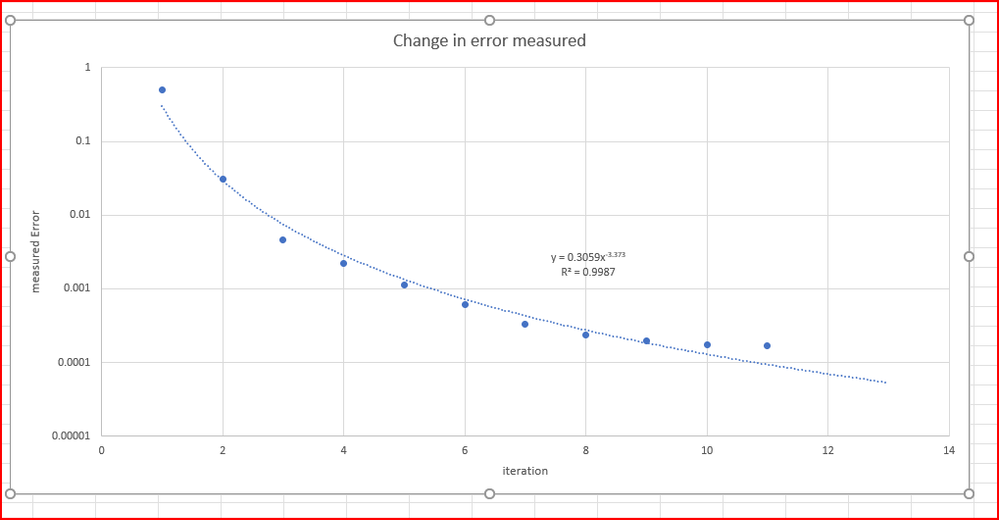
The second interesting element is the convergence on the error limit is following a power regression until it hits a limit of of about 0.00017, if I try and resolve at a lower limit, then the program just goes off in a slowly increasing harmonic cycle for the error.  A slow harmonic rise.  After about 34 iterations it is at about 0.00024 or thereabouts.  

Any ideas, the limit is ok for what I want but it is interesting.  

[JohnNichols]

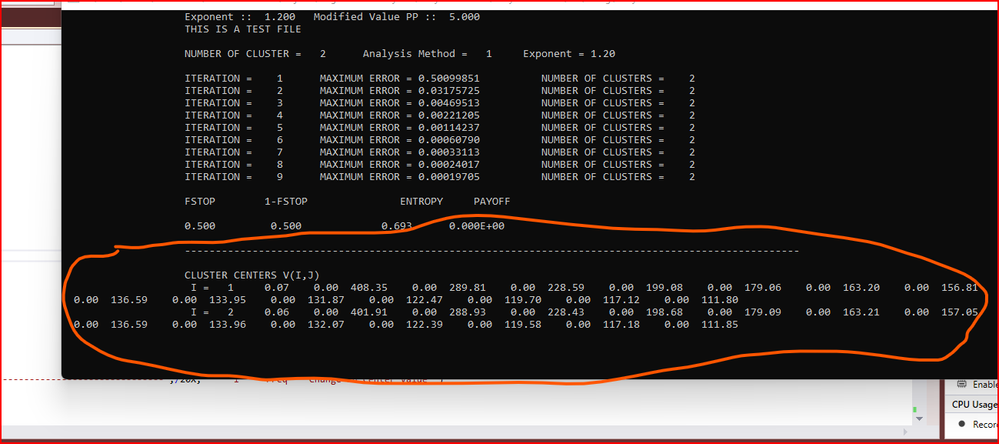
The program prints out the centers for each cluster vector.  It provided a long list of i, j, value, which on an output window in pretty long.  I have 510 input vectors each with 300 dimensions.  I tried to change the output for the cmd window to 15 per line and only look at the first 15.  I had a problem that each line of print gave me two sets of 30.  See picture., for two clusters.  The long printout is fine.  

I then amended the code to just print one at a time and then hold the cursor on the line.  I can do both by changing the value of trial.  

 DO 415 I=1,NCLUS
            if(trial .eq. 0) then
                write(*,4111)I
4111            format(/,20X,i3, 2x,\)
                do j = 1, 15
                    WRITE(*,406) (V(I,J))
                end do
            else            
            WRITE(*,4071) (I,V(I,J),J=1,15)
            end if
415     WRITE(sOUT,404) (I,J,V(I,J),J=1,NDIM)
404     FORMAT(20X, " I = ", I3,3X,"J = ",I3,3X,"V(I,J)= ",F8.4)
4071     FORMAT(20X, " I = ", I3,3X,15(F6.2,2X))
406     FORMAT(F6.1,2x,\)
405     FORMAT(1H ,7(F6.4,3X))

Any ideas on what is my mistake? Line 9 give me the strange output.  If I use line 6 no problems. 

[JohnNichols]

Finally, we have been discussing the topic of numbered do loops.  I am slowly taking out the numbered do loops in this program, but the old problem of 

 do 100 I=1, NCLUS
            DO 100 K=1,NSAMP
                AU=U(I,K)

                F(NCLUS)=F(NCLUS) +AU**2/ANSAMP
                IF (AU) 100,100, 101

101             H(NCLUS)=H(NCLUS)-AU*LOG(AU)/ANSAMP
100     CONTINUE

this example needs two end do the compiler will not cope with one ?   

[jimdempseyatthecove]

You might find it helpful to comment your continue statements as to how you get there. Then edit as necessary

100     CONTINUE ! do 100 I=..., do 100 K=...

Be careful to watch for DO and GOTO to the same CONTINUE. The two pass method will aid in eliminating coding errors (missing ENDIF or mission GOTO label).

Jim Dempsey

[Steve_Lionel]

Shared DO loop continuation is a deleted feature, but as I have said before, compilers continue to support them. Many people didn't understand how they work - a branch to the shared CONTINUE is treated as a branch to the innermost loop's end.

[jimdempseyatthecove]

IIF this is an error value, the error value is made without stating what is the overall "part" size. IOW we would not know the precision of the error.

IIF this is an error ratio, then you would have to consider if the error calculation was derived from a linear, area, or volume measurement. (error, error**-2, error**-3)

If the error calculation is using sqrt or pow, then check to see which variation of the function is used.

In the case of sqrt, should the compiler optimized 1.0/sqrt(x) (and depending on CPU) this may result in 14 bits, 22/23 bits or 28 bits of precision. You can improve the accuracy with adding Newton-Raphson or Taylor series approximation following the initial approximation.

Jim Dempsey

[JohnNichols]

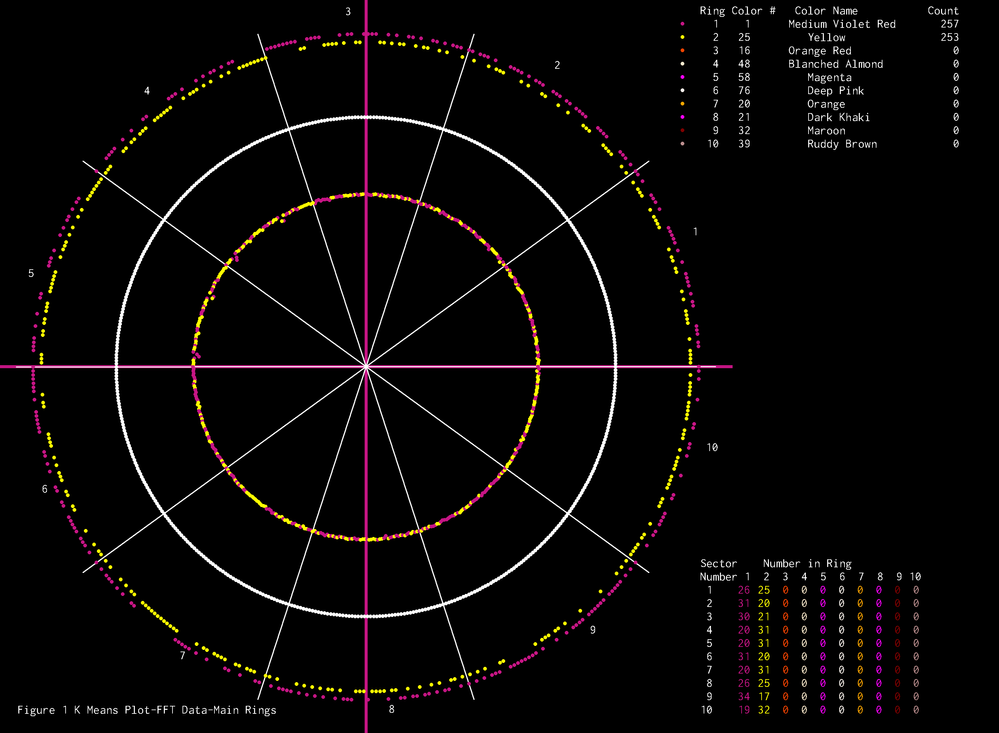
I stumbled across this Fuzzy c Means whilst I was looking at some K Means stuff.  I am slowly unwinding the code and comparing the results to the K Means values.  I had tried a commercial K Means formulation, but it does not allow you to stare into the working elements of the commercial function. The Fortran code allows one to play with the functions, without a lot of work and they are fast.  

The code needs to be commented in greater detail, and the unwinding takes a while as I am looking at the results to see how they fit into the overall analysis.  

The observation about the power function convergence did not occur until I pulled out the detailed printouts that just confused everything and got a decent picture.  I was surprised by the result.  

I will look at the Newton Raphson - but there is a ways to go yet.  

I always thought the shared do loop was a kludge.  

But for 700 lines of Fortran it does the trick. 

The visual output is the key to understanding. 

[JohnNichols]

I was looking at NR technique, then I had a look at the data output for  finding convergence.  The suggested exponent for the least "squares" analysis from the authors is 1.2.  Using this number and the Euclidian distance, the function never crosses zero on some of the 510 vectors.  I moved up to 2 - standard least squares and it crossed zero in a few iterations and solved quite quickly.  

I also got the two other norms working, I need to add the parameter switch so I can see the parameters in the debug window.   The is the result for exponent 2 and the Mahalanobis Norm.  https://en.wikipedia.org/wiki/Mahalanobis_distance  This is actually quite useful in signal analysis.