- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
How to write a Fortran code with a variable number of nested loops.
Thank you.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I can't think of a way to do this. Consider an alternate approach - maybe one that uses a list of actions to take.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
In old Fortran, such nested looping would be accomplished using GOTO statements.
Instead of writing the nested loops explicitly using DO constructs, you can accomplish the same effect by using recursive subroutines or functions. See, for example, this implementation of Quicksort. The recursion can be ended by reaching a count that is computed at run time, or a more general condition may be used.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Could you explain your use case in some detail? Recursion is certainly a versatile tool, but I simply do not understand what you are trying to accomplish
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
For m=2 and m = 3 here it is code:
select case (m)
case (2)
do i1 = 0, 9
do i2 = 0, 9
do i3 = 0, 9
e = v - n(2)*(p(2)+0.1*i2+0.01*i3)
t = 10.0*(e/n(1)-p(1))-0.1*i1
if(dabs(t-dnint(t))<1.0d-8.and.(-0.0001<=t.and.t<9.0001)) then ! if t = 0, 1, 2, 3, ...9
r(1) = p(1)+0.1* t+0.01*i1
r(2) = p(2)+0.1*i2+0.01*i3
go to 91
end if
end do
end do
end do
case (3)
do i1 = 0, 9
do i2 = 0, 9
do i3 = 0, 9
do i4 = 0, 9
do i5 = 0, 9
e = v - n(2)*(p(2)+0.1*i2+0.01*i3) - n(3)*(p(3)+0.1*i4+0.01*i5)
t = 10.0*(e/n(1)-p(1))-0.1*i1
if(dabs(t-dnint(t))<1.0d-8.and.(-0.0001<=t.and.t<9.0001)) then ! if t = 0, 1, 2, 3, ...9
r(1) = p(1)+0.1* t+0.01*i1
r(2) = p(2)+0.1*i2+0.01*i3
r(3) = p(3)+0.1*i4+0.01*i5
go to 91
end if
end do
end do
end do
end do
end do
end select
91 continueI would like a code for some m.
Thank you
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Well, for that sort of situations a solution using recursion is certainly useful. Your current code is a brute-force approach, nothing wrong with that. I would do the recursion on m: the sum up to and including m-1 (for particular choices of ji, ki and li) would provide a new value for V (Vnew = V - sum(i = 1...m-1)) and then you try and find values for jm, km and lm using the nested loop. If you find a solution, print it and be done with it (or continue the search). Once the search space for this level is exhausted, return and proceed with the next iteration. Something like:
recursive subroutine searc( v, m, ... )
do j(i) = 1,9
do k(i) = 1,9
do l(i) = 1,9
vnew = v - ...
if ( vnew > 0 .and. m > 1 ) then
call search( vnew, m-1, ... )
else
print the solution ...
endif
enddo
enddo
enddo Mind you: just a sketch!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Your problem statement does not contain the array p(:), which your code does. Please state what it is, and whether it is an input array, part of the solution, or just a temporary array.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Roy, I have a solution that I am testing, and it has worked on a small problem that I made up.
Please provide a couple of sample problems that you have solved, but don't give me the solution yet. That is, provide values for m, n(), j() and V.
I am asking you for such problems because I may have chosen a rather trivial case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
mecej4,
m = 2
n() j() V = 101646
20 46
3 31
m = 3
n() j() V = 227444
12 78
25 46
6 29- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
In your problem definition (your second post in this thread), you have an inconsistency:
"i, j, k, l, m, n, V are integers > 0" versus "k_i, l_i are integers between [0,9]".
Assuming that k, l are allowed to have 0 as a value, I obtained these two solutions (yes, there can be multiple solutions) for your m = 3 case.
Solution A:
| i | 1 | 2 | 3 |
| k_i | 9 | 1 | 0 |
| l_i | 5 | 0 | 9 |
Solution B:
| i | 1 | 2 | 3 |
| k_i | 0 | 3 | 9 |
| l_i | 0 | 4 | 9 |
If these are acceptable solutions, I'd like to try a problem for a larger m, say, m = 7 or 11. Do you have one?
[I may have made some errors in transcribing the values from my calculation into the tables. If you spot an error, please let me know and I'll rectify.]
By the way, this type of problem is closely related to Cryptarithmetic Problems.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you mecej4,
I wanted to say: i,j(),m,n(),V are integers > 0, and k(), l() are integers between [0,9]
The solutions are correct and I found solution C:
i 1 2 3
------------
k_i 2 3 5
l_i 1 4 7
**************************************************************************************
Here are two other cases:
m = 7
n() j() V = 187321251
98 465
550 269
354 720
806 524
610 328
413 780
642 745
-------------------------
m = 11
n() j() V = 268177985
811 178
263 630
715 434
3 327
534 858
286 389
37 141
568 671
99 202
851 954
382 706- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Here are the solutions (two, for each problem) for your m=7 and m=11 problems.
Problem for m = 7, Solution A
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| k_i | 7 | 9 | 9 | 9 | 5 | 0 | 0 |
| l_i | 8 | 2 | 0 | 0 | 0 | 5 | 1 |
Problem for m = 7, Solution B
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| k_i | 8 | 9 | 8 | 8 | 5 | 1 | 1 |
| l_i | 0 | 0 | 1 | 1 | 1 | 7 | 0 |
Problem for m = 11, Solution A
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| k_i | 0 | 0 | 4 | 0 | 9 | 8 | 3 | 9 | 9 | 9 | 9 |
| l_i | 9 | 9 | 9 | 7 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
Problem for m = 11, Solution B
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| k_i | 9 | 9 | 9 | 9 | 0 | 0 | 9 | 9 | 0 | 9 | 0 |
| l_i | 0 | 0 | 9 | 1 | 9 | 1 | 5 | 9 | 0 | 0 | 9 |
I obtained these solutions using the AMPL solver . The "model" file for m = 11:
# Roy437 test problem.
param M integer := 11;
param V integer := 268177985;
set IDX = 1..M;
var k {IDX} integer >= 0 <= 9;
var l {IDX} integer >= 0 <= 9;
param n {IDX} integer >= 1;
param j {IDX} integer >= 1;
subj to C: sum{i in IDX} (100*j[i]+10*k[i]+l[i])*n[i] = V;
data ;
param: n := 1 811 2 263 3 715 4 3 5 534 6 286 7 37 8 568 9 99 10 851 11 382 ;
param: j := 1 178 2 630 3 434 4 327 5 858 6 389 7 141 8 671 9 202 10 954 11 706 ;
option solver ilogcp; solve;
display {i in IDX} (k[i],l[i]);
You may use the online NEOS server if you do not wish to obtain the AMPL demo package and install it on your machine. If you use the server, use the three files in the attached zip.
If obtaining the solution is sufficient, you may use AMPL on your PC or on the NEOS server. If you wish to call the AMPL solver from a Fortran or C program, a number of methods may be tried, but mating a Fortran program to the AMPL solvers is non-trivial.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you very much mecej4.
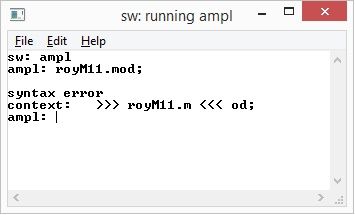
The solutions are good, I checked them. I installed the AMPL Command Line download for Windows program, but it gives me an error. Please, can you tell me what commands to give or how to proceed with the three files royM11.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
There are a number of tutorials for running AMPL from the command line, or using the Eclipse-based IDE, and the AMPL language itself. For now, since you have AMPL installed locally, the following is the simplest approach:
- open a CMD window, and set the path to include the directory containing AMPL.EXE.
- in your working directory, copy the code in the box in my post above (not the the files in the zip, which are for NEOS) to, say, M11.mod .
- enter the command
ampl M11.mod
You will see the results displayed at the console.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thanks mecej4,
I did it. Can I redirect the result to a file?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Of course. The command can be
ampl M11.mod > M11.outYou can then type the M11.out file, open it in Notepad or another editor, Word, etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you very much mecej4,
Now it is very clear what I have to do, I will test the program for values greater than 11.
Thousands of thanks, good health and happiness.
You are a great man !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Mecej4,
One more question, can I find all the solutions?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I do not know much about the mathematical nature of such problems, but I think that in general we do not know if a solution exists at all, or how many solutions exist. From the typical solver's point of view, it will either give one solution if it can find one, or announce failure, and then terminate. A different solver may find a different solution. In fact, for the cases where I gave two solutions, I used the ILOGCP solver for one and the Gurobi solver for the other.
Do you have a criterion to mark one solution as being better than another? AMPL does have a provision for specifying that the solution elements be all distinct in value.
I appreciate your kind words.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page