- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
program solve
use lapack95
real(8) A(3,3),B(3),work(999)
integer m/3/,n/3/,nb/3/,lwork(999),info,nrhs/3/
n=n
call dgels("N", 3, 3, 3, A, 3, b, 3 ,work, lwork, info)
! dgels(trans, m, n, nrhs, a, lda, b, ldb, work, lwork, info)
read(*,*)
end program
I get this weird missing entry point - see screen shot
I am pointing to the MKL library in my project properties, apparently it DOES find
the DGELS routine.
The program does not even start. I have not bothered to put in numbers as yet.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
My current license would not allow me to use any of the products from 2016.
So I downloaded the latest Fortran from 2017, and of course had to use Visual studio 2013
However, I get the same error message. Why does it think that my EXE is a dynamic link library?
Isn't it supposed to look for the entry point elsewhere ?
BTW, as soon as I remove the reference to the MKL routine, this error goes away.
I had to move to a 64 bit INTEL CPU because I lost the other computer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The missing symbol is defined in "mkl_intel_thread.dll". I think you must have linked your program with a newer version of mkl .lib file but have an old version of mkl .dll file in your PATH setting.
Thanks,
Xiaoping Duan
Intel Customer Support
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I am not sure what you are trying to do. Are you trying to solve three simultaneous linear equations with one right hand side vector? If so, many of the arguments that you pass to DGELS are wrong. Many arguments are not even defined before the call.
Lapack and BLAS routines do only limited checking of the input data. To get them to work, one has to read the documentation and make sure that the arguments passed are of the proper types, kinds and sizes.
You have "use lapack95", but your subroutine call uses nothing in Lapack95.
Finally, if you want specific help on error messages that you saw, you must report exactly what steps you took before you received those messages. How did you compile, what options did you use and what data did you run the program with? What answer do you expect? Without such specific details, code such as the one that you posted simply reinforces the adage "garbage in, garbage out".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I am NOT TRYING TO SOLVE LINEAR EQUATIONS ! ! ! ! ! !
IT IS A LEAST SQUARES PROBLEM.
and the library is a LAPACK routine, not a BLAS routine.
DGELS, SGES, GELS, etc. are in that library.
It is written up under LAPACK routines.
To call that, I used Steve Lionel's recommendation, to set "use MKL" under fortran > libraries.
The argument list is exactly as defined in the GELS write-up, under LAPACK library routines.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
In that case, first take a look at the example provided at ...\compilers_and_libraries_2017.1.143\windows\mkl\examples\lapack95\source\gels.f90, if you want to use the Fortran 9x interface, or the similar file dgelsx.f in ...\mkl\examples\lapackf\source. Each of these is meant to be run with input data in files in the ...\mkl\examples\lapack{f | 95}\data folders.
If you have not unpacked the MKL example Zip files after installation, do so first, before trying to locate the files that I mentioned.
In MKL, Lapack, BLAS, FFT and many other routines are all packaged into a single library. Different versions of the MKL library exist for sequential/parallel, 4-byte/8-byte integers, 32-bit/64-bit, etc., combinations.
Lapack calls can be complex, particularly if calling from a language other than Fortran. It is better to start with one of the working examples provided and modify that rather than to start from scratch.
I find it odd that you are calling GELS with a square matrix, for which the least squares solution is the same as that given by Gaussian elimination (apart from floating point loss of precision). The Q-R algorithm used by GELS is not as efficient as the L-U factorization used by GESV, so if you are sure that the matrices you have are square (i.e., number of observations m = number of unknown model parameters n), use GESV instead.
The argument list is exactly as defined in the GELS write-up, under LAPACK library routines.
Not quite. Look again, more carefully. The fourth and tenth arguments are wrong.
MODERATOR: Please consider moving this thread into the MKL forum.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Bill, here is an example to show that for a square matrix of full rank GESV and GELS yield the same solution. In other words, for M = N and A of full rank, the sum of the squares of the residuals from the least squares solution is exactly zero (with infinite precision floating point; you may wish to compute and print the SSQR for the example).
program xgesv
use lapack95
implicit none
integer, parameter :: M = 4, N = 4, NRHS = 1
double precision :: A(M,N) = reshape( [ &
1.80, 2.88, 2.05, -0.89, &
5.25, -2.95, -0.95, -3.80, &
1.58, -2.69, -2.90, -1.04, &
-1.11, -0.66, -0.59, 0.80], [M,N])
double precision :: B(N,NRHS) = [9.52, 24.35, 0.77, -6.22], &
BS(N,NRHS), AS(M,N)
!
A = transpose(A)
AS = A ! save for reuse later
BS = B
call gesv(A,B)
write(*,'(1x,A,2x,4F10.4)')'Solution from GESV: ',B(1:N,1)
A = AS ! restore saved matrices
B = BS
call gels(A,B)
write(*,'(1x,A,2x,4F10.4)')'Solution from GELS: ',B(1:N,1)
end program xgesv
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Well, in my case, I HAVE AN OVER DETERMINED SYSTEM, SO GESV would not work anyway.
And the matrix does not have to be square, either.
The issue is: why wont the Visual Studio 2013 link properly to these routines ?
I dont see this with an earlier VS, like 2010.
Apparently they didn't test this stuff first ?
If there is something special we are supposed to do with VS2013, they didn't give us a clue how - - - -
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Every user of Intel Fortran is not also a user of MKL, and every VS project does not require MKL routines. For years, MKL used to be a separately marketed product. There is a one-time configuration that you need to do, for each combination of VS+compiler+MKL.
See https://software.intel.com/en-us/articles/intel-math-kernel-library-intel-mkl-compiling-and-linking-with-microsoft-visual-cc .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
That article does not address my problem at all.
First of all, I am using VS 2013, which it does not mention.
Secondly, it does not appear to address Fortran users.
We need an article that specifically says:
What do we need to put into the Visual 2013 setup,
in order to use the MKL routines?
Are there other libraries we have to add to the MKL one?
I did not have any problem using those on my 32-bit CPU machine.
Seems like a starightforward question, I just need a straightforward intelligent answer,
rather than gibberish.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Create a new VS Fortran Console project.
- Right-click on Source Files in the Solution Explorer, select Add Existing Item, and add the source file(s) needed.
- Right-click on the project (Console1, if you did not specify another name), select Properties--Fortran--Libraries and select a suitable option for Intel Math Kernel Library other than No.
For more details, see https://software.intel.com/en-us/articles/intel-math-kernel-library-intel-mkl-compiling-and-linking-with-microsoft-visual-cc .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
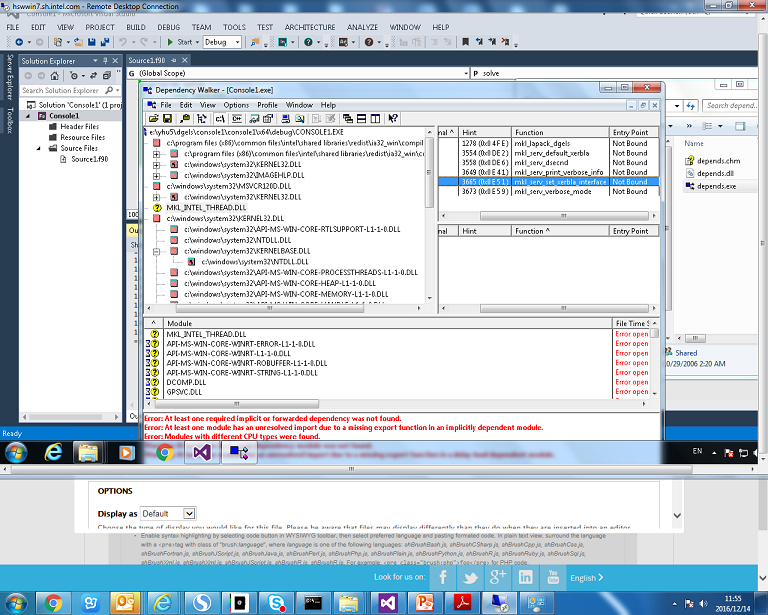
Hi Billsincl,
is there other version mkl install on your machine? I did a quick test with your code, but I can't reproduce the problem. The symbol mkl_serv_set_xerbla_interface was defined in mkl_intel_thread.dll.
So the key for your problem is what MKL path in your environment
Open your computer's property ( from windows menu) => advanced system setting => Advanced => environment variable => Edit system variables PATH, add C:\Program Files (x86)\IntelSWTools\compilers_and_libraries_2017.1.143\windows\redist\intel64_win at first place.
then restart your MSVS 2013 project to make sure the environment valid.
and see if the error will gone?
And if possible, please use dependency walker to check which the MKL dll and path are using.
for example, below is the dependency walker result of the test, where no path was setting for mkl_intel_thread.dll.
Best Regards
Ying
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page