- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good afternoon,
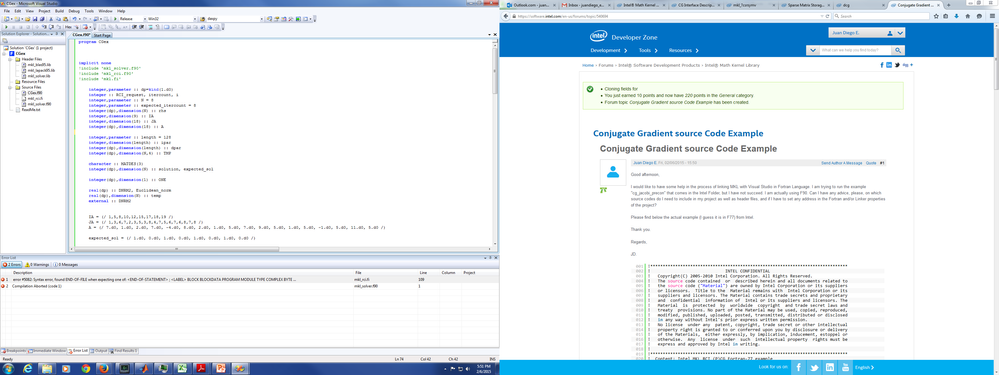
I would like to have some help in the process of linking MKL with Visual Studio in Fortran Language. I am trying to run the example "cg_jacobi_precon" that comes in the Intel Folder, but I have not succeed. I am actually using F90. Can I have any advice, please, on which source codes do I need to include in my project as well as header files, and if I have to set any address in the Fortran and/or Linker properties of the project?
Please find below the actual example (I guess it is in F77) from Intel.
Thank you.
Regards,
JD.
!*******************************************************************************
! INTEL CONFIDENTIAL
! Copyright(C) 2005-2010 Intel Corporation. All Rights Reserved.
! The source code contained or described herein and all documents related to
! the source code ("Material") are owned by Intel Corporation or its suppliers
! or licensors. Title to the Material remains with Intel Corporation or its
! suppliers and licensors. The Material contains trade secrets and proprietary
! and confidential information of Intel or its suppliers and licensors. The
! Material is protected by worldwide copyright and trade secret laws and
! treaty provisions. No part of the Material may be used, copied, reproduced,
! modified, published, uploaded, posted, transmitted, distributed or disclosed
! in any way without Intel's prior express written permission.
! No license under any patent, copyright, trade secret or other intellectual
! property right is granted to or conferred upon you by disclosure or delivery
! of the Materials, either expressly, by implication, inducement, estoppel or
! otherwise. Any license under such intellectual property rights must be
! express and approved by Intel in writing.
!
!*******************************************************************************
! Content: Intel MKL RCI (P)CG Fortran-77 example
!
!*******************************************************************************
!---------------------------------------------------------------------------
! Example program for solving symmetric positive definite system of equations.
! Full case: full functionality of RCI (P)CG is used.
!---------------------------------------------------------------------------
PROGRAM rci_pcg_f77_test_3
IMPLICIT NONE
INCLUDE 'mkl_rci.fi'
!---------------------------------------------------------------------------
! Define arrays for the upper triangle of the coefficient matrix and
! preconditioner as well as an array for rhs vector
! Compressed sparse row storage is used for sparse representation
!---------------------------------------------------------------------------
INTEGER N, RCI_request, itercount, expected_itercount, i
PARAMETER (N=8)
PARAMETER (expected_itercount=8)
DOUBLE PRECISION rhs(N)
INTEGER IA(9)
INTEGER JA(18)
DOUBLE PRECISION A(18)
! Fill all arrays containing matrix data.
DATA IA /1,5,8,10,12,15,17,18,19/
DATA JA
1 /1, 3, 6,7,
2 2,3, 5,
3 3, 8,
4 4, 7,
5 5,6,7,
6 6, 8,
7 7,
8 8/
DATA A
1 /7.D0, 1.D0, 2.D0, 7.D0,
2 -4.D0, 8.D0, 2.D0,
3 1.D0, 5.D0,
4 7.D0, 9.D0,
5 5.D0, 1.D0, 5.D0,
6 -1.D0, 5.D0,
7 11.D0,
8 5.D0/
!---------------------------------------------------------------------------
! Allocate storage for the solver ?par and the initial solution vector
!---------------------------------------------------------------------------
INTEGER length
PARAMETER (length=128)
INTEGER ipar(length)
DOUBLE PRECISION dpar(length),TMP(N,4)
!---------------------------------------------------------------------------
! Some additional variables to use with the RCI (P)CG solver
!---------------------------------------------------------------------------
CHARACTER MATDES(3)
DOUBLE PRECISION solution(N)
DOUBLE PRECISION expected_sol(N)
DATA expected_sol/1.D0, 0.D0, 1.D0, 0.D0, 1.D0, 0.D0, 1.D0, 0.D0/
DOUBLE PRECISION ONE
DATA ONE/1.D0/
DOUBLE PRECISION DNRM2, Euclidean_norm, temp(N)
EXTERNAL DNRM2
!---------------------------------------------------------------------------
! Initialize the right hand side through matrix-vector product
!---------------------------------------------------------------------------
CALL MKL_DCSRSYMV('U', N, A, IA, JA, expected_sol, rhs)
!---------------------------------------------------------------------------
! Initialize the initial guess
!---------------------------------------------------------------------------
DO I=1, N
solution(I)=0.D0
ENDDO
MATDES(1)='D'
MATDES(2)='L'
MATDES(3)='N'
!---------------------------------------------------------------------------
! Initialize the solver
!---------------------------------------------------------------------------
CALL dcg_init(N, solution,rhs, RCI_request,ipar,dpar,TMP)
IF (RCI_request .NE. 0 ) GOTO 999
!---------------------------------------------------------------------------
! Set the desired parameters:
! INTEGER parameters:
! set the maximal number of iterations to 100
! LOGICAL parameters:
! run the Preconditioned version of RCI (P)CG with preconditioner C_inverse
! DOUBLE PRECISION parameters
! -
!---------------------------------------------------------------------------
ipar(5)=100
ipar(11)=1
!---------------------------------------------------------------------------
! Check the correctness and consistency of the newly set parameters
!---------------------------------------------------------------------------
CALL dcg_check(N,solution,rhs,RCI_request,ipar,dpar,TMP)
IF (RCI_request .NE. 0 ) GOTO 999
!---------------------------------------------------------------------------
! Compute the solution by RCI (P)CG solver
! Reverse Communications starts here
!---------------------------------------------------------------------------
1 CALL dcg(N,solution,rhs,RCI_request,ipar,dpar,TMP)
!---------------------------------------------------------------------------
! If RCI_request=0, then the solution was found according to the requested
! stopping tests. In this case, this means that it was found after 100
! iterations.
!---------------------------------------------------------------------------
IF (RCI_request .EQ. 0) THEN
GOTO 700
!---------------------------------------------------------------------------
! If RCI_request=1, then compute the vector A*TMP(:,1)
! and put the result in vector TMP(:,2)
!---------------------------------------------------------------------------
ELSEIF (RCI_request .EQ. 1) THEN
CALL MKL_DCSRSYMV('U', N, A, IA, JA, TMP, TMP(1,2))
GOTO 1
!---------------------------------------------------------------------------
! If RCI_request=2, then do the user-defined stopping test: compute the
! Euclidean norm of the actual residual using MKL routines and check if
! it is less than 1.D-8
!---------------------------------------------------------------------------
ELSEIF (RCI_request .EQ. 2) THEN
CALL MKL_DCSRSYMV('U', N, A, IA, JA, solution, temp)
CALL DAXPY(N,-1.D0,rhs,1,temp,1)
Euclidean_norm = DNRM2(N,temp,1)
IF (Euclidean_norm .GT. 1.D-8) THEN
!---------------------------------------------------------------------------
! The solution has not been found yet according to the user-defined stopping
! test. Continue RCI (P)CG iterations.
!---------------------------------------------------------------------------
GOTO 1
ELSE
!---------------------------------------------------------------------------
! The solution has been found according to the user-defined stopping test
!---------------------------------------------------------------------------
GOTO 700
END IF
!---------------------------------------------------------------------------
! If RCI_request=3, then compute apply the preconditioner matrix C_inverse
! on vector TMP(:,3) and put the result in vector TMP(:,4)
!---------------------------------------------------------------------------
ELSEIF (RCI_request .EQ. 3) THEN
CALL MKL_DCSRSV('N', N, ONE, MATDES,
& A, JA, IA, IA(2), TMP(1,3), TMP(1,4))
GOTO 1
ELSE
!---------------------------------------------------------------------------
! If RCI_request=anything else, then dcg subroutine failed
! to compute the solution vector: solution(N)
!---------------------------------------------------------------------------
GOTO 999
ENDIF
!---------------------------------------------------------------------------
! Reverse Communication ends here
! Get the current iteration number
!---------------------------------------------------------------------------
700 CALL dcg_get(N,solution,rhs,RCI_request,ipar,dpar,TMP,
& itercount)
!---------------------------------------------------------------------------
! Print solution vector: solution(N) and number of iterations: itercount
!---------------------------------------------------------------------------
WRITE(*, *) ' The system has been solved '
WRITE(*, *) ' The following solution obtained '
WRITE(*,800) (solution(i),i =1,N)
WRITE(*, *) ' expected solution '
WRITE(*,800)(expected_sol(i),i =1,N)
800 FORMAT(4(F10.3))
WRITE(*,900)(itercount)
900 FORMAT(' Number of iterations: ',1(I2))
DO I=1,N
expected_sol(I)=expected_sol(I)-solution(I)
ENDDO
Euclidean_norm=DNRM2(N,expected_sol,1)
!---------------------------------------------------------------------------
! Release internal MKL memory that might be used for computations
! NOTE: It is important to call the routine below to avoid memory leaks
! unless you disable MKL Memory Manager
!---------------------------------------------------------------------------
CALL MKL_FREEBUFFERS
IF (itercount.EQ.expected_itercount .AND.
1 Euclidean_norm.LE.1.0D-12) THEN
WRITE( *,'(A,A)') 'This example has successfully PASSED',
1 ' through all steps of computation!'
STOP 0
ELSE
WRITE( *,'(A,A,A,I5,A,A,A,E12.5,A)') 'This example may have',
1 ' FAILED as either the number of iterations differs from the',
2 ' expected number of iterations ',expected_itercount,' or the',
3 ' computed solution differs much from the expected solution (',
4 'Euclidean norm is ',Euclidean_norm,'), or both.'
STOP 1
ENDIF
!---------------------------------------------------------------------------
! Release internal MKL memory that might be used for computations
! NOTE: It is important to call the routine below to avoid memory leaks
! unless you disable MKL Memory Manager
!---------------------------------------------------------------------------
999 WRITE( *,'(A,A)') 'This example FAILED as the solver has',
1 ' returned the ERROR code', RCI_request
CALL MKL_FREEBUFFERS
STOP 1
END
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Here is one possible source of error: you apparently are comparing solutions for linear equations with a symmetric indefinite matrix. In the GMRES version of your code, you initialize the (rowidx, col, val) arrays for the upper triangular part of the matrix. The solver routines that you call, however, expect the lower triangular part to be filled in, as well, because these routines (with names containing GE rather than SYM) have to work with unsymmetric matrices too. In effect, then, the Pardiso version gives the solution for the symmetric matrix whereas the GMRES version gives the solution for an upper triangular, unsymmetric matrix. Naturally, the two solutions will not agree.
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Please find attached a picture on which you can see what I have added to my project and the error that I have when trying to compile it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The file name is cg_jacobi_precon.f (if you are using the Windows explorer, you may want to set the folder options to make file suffixes visible). The file suffix is .f, as it should be for a fixed format Fortran source file. There are two errors in the listing that you posted: change the two instances of MKL_FREEBUFFERS to MKL_FREE_BUFFERS.
The screenshots that you attached are not useful because only a part of the source code is shown. At any rate, the source code is provided by Intel in the MKL examples directory or in the examples_core_f.zip file and you can use the provided file without modification.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good afternoon,
Thank you very much mecej4. I will try and change those things you mentioned and check if it works now. In my case I would need to solve a system of equations a lot of times one after the other (it is a transients problem), so everytime I will need to call the function for: initialize, check, and solve? I guess this calls consume a lot of time dont they?
Thank you.
JD
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Let us represent the equations by A.x = b. From what you said, x and b vary with time. But how about A? If A is constant, you only need to factorize it once and use the solution phase of Pardiso from then on, as many time steps as you wish.
If A varies, as well, then the question is whether only certain parts of A change and if you know the exact nature of that change. If the values in A change but the locations of the nonzero elements do not change with time, then all the instances of A(t) are structurally the same, and some economy can be achieved by knowing that.
The more you know the nature of your problem, the better will you be able to choose an appropriate solution strategy.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good afternoon,
Yes, exactly. In my case both A changes (because the main diagonal terms has the time variable there) and B changes as well because this will depend on the previous time-step calculation. The structure of the matrix is exactly the same. So in this case which calls should I do to Pardiso (if I decicde to use this solver and no RCI ISS) at each time step?
I actually just began another forum because I am also trying to figure out which is the best solver for my simulations. Can you please see the forum: PARDISO vs LAPACK Performance ? If you see the code there, you can notice that I am implementing Pardiso with phase 13 (analyze, factorize and solve) at each time step. I dont know if maybe this is the reason why Pardiso is taking almost twice the time vs LAPACK.
Thank you very much mecej4 for your reply. I would appreciate if you can let me know what is the best implementation of Pardiso in this case (please look at the other forum, or if you want I can just post everything here as well)
Regards,
J.D
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Pardiso takes a 'phase' argument which is a two digit number. The first digit is the starting phase and the second digit is the terminating phase. Thus, 13 is equivalent to 11, 22, 33 in sequence. Of these three, 22 is the most time consuming. For the problem that you described, phase 11 needs to be done only once. The other two phases have to be performed each time step. The savings from doing phase 11 only once may not be large, but definitely worthwhile since the cost of reorganizing your code to do so is very little. In your code in the other thread, you have use 11, 22 and then 13, which amounts to doing 11 and 22 twice each step -- unnecessary and inefficient. If your matrix remains structurally constant, there is no need to deallocate Pardiso memory between time steps.
As to the choice between Lapack and Pardiso, there is no contest. Most Lapack linear solvers are for dense matrices. If your matrix is derived by discretizing a partial differential equation, it will be sparse, possibly banded. If your matrix is banded, Lapack does have some suitable routines, but again Pardiso is probably going to be faster.
There other sparse solvers available (SuperLU, WSMP, UMFPack, etc.) and it is worthwhile for you to learn about their characteristics and ascertain which sparse solver best suits your application.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good morning mecej4,
Thank you very much for your observations. I will modify the code accordingly and check if it actually ran faster with Pardiso. If it is not the case, do you think one of the reasons might be that Lapack is actually better for matrices not that big? maybe if the size of my matrices are on the order of 20000 to 45000 I would expect Pardiso to be faster?
Thank you.
Regards,
J.D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good afternoon,
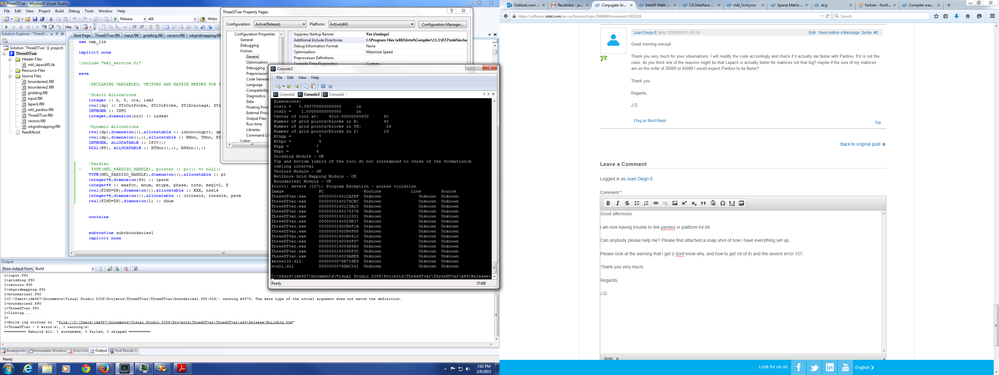
I am now having trouble to link pardiso in platform 64 bit.
Can anybody please help me? Please find attached a snap shot of how I have everything set up.
Please look at the warning that I get (I dont know why, and how to get rid of it) and the severe error 157.
Thank you very much,
Regards,
J.D.
if (ParTLapF) then
allocate(pt(64), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate pt(64), in boundaries1 module ***"
do i = 1,64
pt( i )%DUMMY = 0
end do
maxfct = 1
mnum = 1
mtype = 2
allocate(nzele((size(Tz))+(size(Tth))+(size(Tr))+(Nz*Nth*Nr)), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate nzele((size(Tz))+(size(Tth))+(size(Tr))+(Nz*Nth*Nr)), in boundaries1 module ***"
allocate(colnzele((size(Tz))+(size(Tth))+(size(Tr))+(Nz*Nth*Nr)), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate colnzele((size(Tz))+(size(Tth))+(size(Tr))+(Nz*Nth*Nr)), in boundaries1 module ***"
allocate(innzele((Nz*Nr*Nth)+1), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate innzele((Nz*Nr*Nth)+1), in boundaries1 module ***"
cta = 0
ctt = 0
!$OMP PARALLEL DO
do i = 1,(Nz*Nr*Nth)
do j = 1,(Nz*Nr*Nth)
if ((j >= i) .AND. (abs(TMnn(i,j)) > 0.0)) then
ctt = ctt + 1
nzele(ctt) = TMnn(i,j)
colnzele(ctt) = j
if (j == i) then
cta = cta + 1
innzele(cta) = ctt
end if
end if
end do
end do
!$OMP END PARALLEL DO
innzele(size(innzele)) = (size(Tz))+(size(Tth))+(size(Tr))+(Nz*Nth*Nr)+1
allocate(perm(Nz*Nr*Nth), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate perm(Nz*Nr*Nth), in boundaries1 module ***"
do i = 1,(Nz*Nr*Nth)
perm(i) = 1
end do
nrhs = 1
do i = 1,64
iparm(i) = 0
end do
iparm(1) = 1 ! no solver default
iparm(2) = 2 ! fill-in reordering from METIS
iparm(4) = 0 ! no iterative-direct algorithm 0 or 62 (iterative preconditioning)
iparm(5) = 0 ! no user fill-in reducing permutation
iparm(6) = 1 ! =0 solution on the first n compoments of x
iparm(8) = 0 ! numbers of iterative refinement steps
iparm(10) = 8 ! perturbe the pivot elements with 1E-13
iparm(11) = 0 ! use nonsymmetric permutation and scaling MPS
iparm(13) = 0 ! maximum weighted matching algorithm is switched-off (default for symmetric). Try iparm(13) = 1 in case of inappropriate accuracy
iparm(14) = 0 ! Output: number of perturbed pivots
iparm(24) = 0 ! Parallel factorization control: 1 -> two level factorization algorithm. 0 -> classic algorithm for factorization
iparm(25) = 0 ! 0 -> parallel algorithm for the solve step. 1 -> sequential forward and backward solve
msglvl = 0 !not printing statistical information
allocate(XXX(Nz*Nr*Nth), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate XXX(Nz*Nr*Nth), in boundaries1 module ***"
E = 0
end if
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
phase = 13
call pardiso_D_64 (pt, maxfct, mnum, mtype, phase, Nz*Nr*Nth, nzele, innzele, colnzele, perm, nrhs, iparm, msglvl, RHSnn, XXX, E)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
Could you please replace pardiso_D_64 to pardiso and set iparm(27) and msglvl to 1? There could be a problem in matrix structure
Thanks,
Alex
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
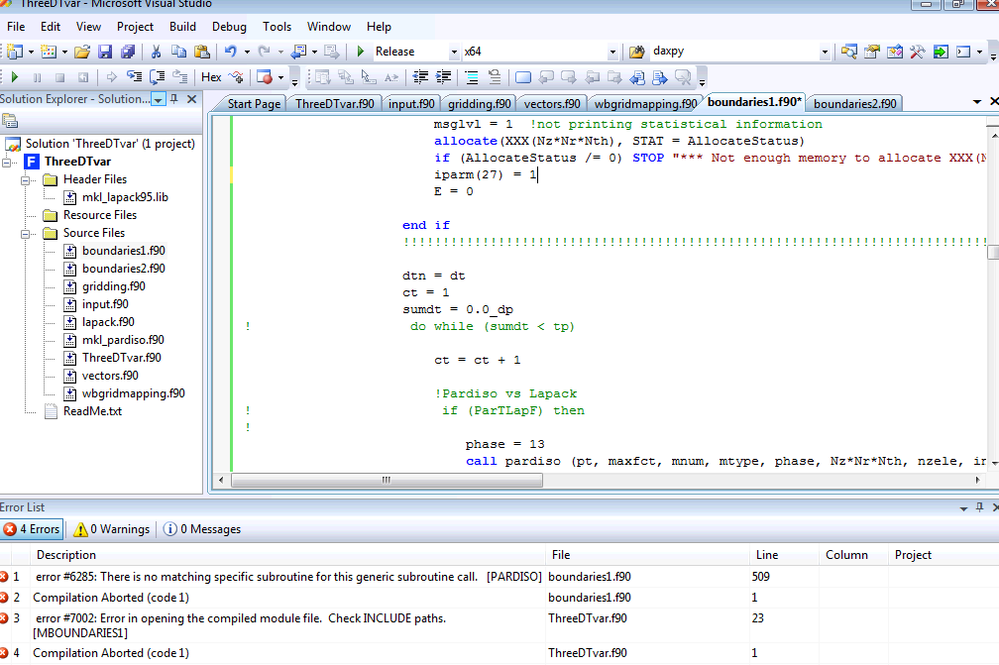
Hi Alex,
Thanks for your prompt reply.
This is what I got when I modify what you mentioned. What should I do?
J.D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
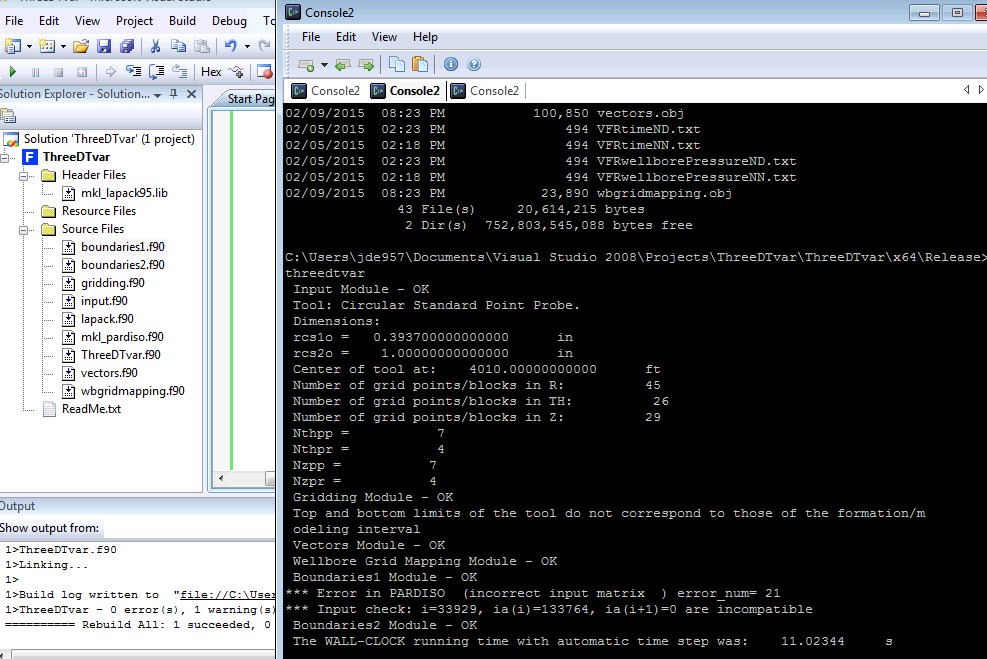
Hi Alex,
I decided to run it again with pardiso_D_64, but setting the other two parameters you mentioned to 1. And this is the error that I got. What does it mean? how can I fix it?
Thank you very much.
J.D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
Which name of include file you use in your example?
About this problem - matrix checker show the issue in your ia array, namely ia(33930) is equal to zero. Pardiso decide that size of your matrix is greater than 33928 and its values is incorrect. What value of n you set in pardiso?
Thanks,
Alex
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi Alex,
Thank you for your reply. I checked that and I corrected the mistake, which actually was because I implemented a OMP PARALLEL DO loop, and it did something I did not want to, so once I performed the a normal do loop, I got the answer.
Thank you and regards,
J.D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good afternoon,
I would like to ask about the FGMRES with ILU0 Preconditioner solver. I have a code on which I implement LAPACK, PARDISO, and now I would like to check the performance with this iterative solver. LAPACK and PARDISO gave me exactly the same results (as expected) and Pardiso performed 15% to 20% faster than LAPACK for large systems (34000 elements) and around 50-100 time steps. However, when I implemented the FGMRES solver, it actually gave me a completely wrong solution. So I went one step back and first made the example to work, and it did. When I tried to implement the Pardiso example into FGMRES, it actually again gave me a completely different solution. I would like to know, why is this happening? Do I have something wrong? In addition I would like to know what are the best parameters (IPAR and DPAR) I should use for a ill-posed symmetric large (35000 or more) system when using FGMRES?
Please find attached the corresponding documents (Pardiso example and FGMRES example).
Thank you for your reply.
Regards,
J.D.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You attached only the .SLN files, which are of no use -- we need the source code, along with any data and a list of the compiler options used. You talk of "the Pardiso example", but the MKL examples/solverf/source directory contains six Pardiso examples. Similarly, there are three GMRES related examples. Which of these did you modify?
With all these uncertainties, and without seeing the code, it is not possible to respond.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good morning mecej4,
Perfect. Please find attached the source codes for both examples (I am implementing modules, as I was trying to emulate the situation in which I really need to implement this solvers). The first two source codes correspond to PardisoEX (PardisoEX.f90 and input.f90) and the last two source codes correspond to FGMRESex3 (FGMRESex3.f90 and input_0.f90).
I am comparing: pardiso_sym_f90 and dcsrilu0_exampl2
I am using 64 bit platform release mode. Machine: 32 GB RAM, Intel Core i7 3.4 GHz. 4 cores = 8 threads. Visual Studio 2008. Fortran 90. Intel Compiler 11.1-072
On both cases - Properties:
* I included directory in Fortran/general: "C:\Program Files (x86)\Intel\Compiler\11.1\072\mkl\include"
* Fortran/general/Optimization: Maximize speed
* Fortran/Preprocessor/Default Include and Use Path: Source File directory
* Fortran/Preprocessor/OpenMP Conditional Compilation: Yes
* Fortran/Libraries/run time library: Multithread
* Fortran/Libraries/Use Intel Math Kernel Library: Parallel
*Linker/General/Link library dependencies: Yes
* Linker/Manifest File/Generate manifest file: No
In the Pardiso example I also manually included the following:
* In the Header Files Folder: mkl_lapack95.lib
* In the Source Files Folder: lapack.f90 and mkl_pardiso.f90 in addition to the two source files attached to this message.
In the FGMRES example I also manually included the following:
* In the Header Files Folder: mkl_lapack95.lib and mkl_lapack95_lp64.lib
* In the Source Files Folder: lapack.f90, mkl.fi and mkl_rci.fi
Thank you very much for the support.
Regards,
J.D
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Here is one possible source of error: you apparently are comparing solutions for linear equations with a symmetric indefinite matrix. In the GMRES version of your code, you initialize the (rowidx, col, val) arrays for the upper triangular part of the matrix. The solver routines that you call, however, expect the lower triangular part to be filled in, as well, because these routines (with names containing GE rather than SYM) have to work with unsymmetric matrices too. In effect, then, the Pardiso version gives the solution for the symmetric matrix whereas the GMRES version gives the solution for an upper triangular, unsymmetric matrix. Naturally, the two solutions will not agree.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good afternoon mecej4,
Thank you very much for your input! I did not think about that. I will modify the inputs accordingly and will come back to you with the results. As you said, I am actually trying to solve a system of equations that comes from a finite difference discretization of a PDE, which results in a symmetric diagonally dominant matrix (with high condition number as the CG iterative solver from MKL did not work giving me the error that the matrix was almost indefinite).
Thanks again.
Regards,
J.D
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good morning mecej4,
I was busy working these days in other things, and right now I tried what you told me with the Intel examples, and it actually worked! That was my mistake, I was inputting the triangular part of the matrix to the FMGRES solver whereas it should have been the full symmetric matrix.
Thanks a lot for your help!
Regards,
J.D
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Good afternoon,
I am now facing another issue with the FGMRES Solver. It is working for a one-time use; however, I need to call FGMRES at multiple time steps and the executable never stops. I was wondering if it has to be with IPAR(15) (which I do not know very clear what is the restarted version or non-restarted version). Can anybody help me out with this issue?
Please find the script where I am calling a subroutine in a module. This subroutine contains the FGMRES algorithm and calls to corresponding functions. The link is fine (it is running) however, when I run multiple time steps I got what you see in the picture(s) contained in the attached document (it can be seen the executable has not stopped yet).
Thank you.
Regards,
J.D.
module mboundaries
USE *****
implicit none
save
DECLARING VARIABLES ******
contains
subroutine subrboundaries
implicit none
!SOLVING SYSTEM OF EQUATIONS - USING LAPACK - GBSV OR PARDISO
allocate(tmp2(Nz), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single phase flow rate temporal vector to get as output Pwf for all times at the middle of the packer ***"
tmp2 = abs(czp-dzgp)
idxx2 = minloc(tmp2)
idx2 = idxx2(1)
allocate(IPIV(Nz*Nr), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single phase flow rate pivoting vector as per LAPACK - GBSV subroutine, if N-N ***"
IPIV = 0
allocate(BTMnni(((2*Nz)+Nz+1),(Nz*Nr)), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single phase flow rate 'initial' banded TM Matrix as per LAPACK - GBSV subroutine requirements, if N-N ***"
allocate(RHSnn((Nz*Nr),1), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single phase flow rate right hand side vector of system of equations as per LAPACK - GBSV subroutine, if N-N ***"
BTMnni = BTMnn
RHSnn(:,1) = matmul(BMnn,Psfr(:,1)) - NNSSV
allocate(DeltaP(Nz*Nr), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate DeltaP vector to get DPMAX, if N-N ***"
DeltaP = 0.0_dp
if (ParTLapF) then
!FMGRES
allocate(nzelef((2*size(Tz))+(2*size(Tr))+(Nz*Nr)), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate nzelef((size(Tz))+(size(Tth))+(size(Tr))+(Nz*Nth*Nr)), in boundaries1 module ***"
allocate(colnzelef((2*size(Tz))+(2*size(Tr))+(Nz*Nr)), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate colnzelef((size(Tz))+(size(Tth))+(size(Tr))+(Nz*Nth*Nr)), in boundaries1 module ***"
allocate(innzelef((Nz*Nr)+1), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate innzelef((Nz*Nr*Nth)+1), in boundaries1 module ***"
cta = 0
ctt = 0
do i = 1,(Nz*Nr)
ct = 1
do j = 1,(Nz*Nr)
if (abs(TMnn(i,j)) > 0.0) then
ctt = ctt + 1
nzelef(ctt) = ATMnn(i,j)
colnzelef(ctt) = j
if (ct == 1) then
cta = cta + 1
innzelef(cta) = ctt
ct = 0
end if
end if
end do
end do
innzelef(size(innzelef)) = (2*size(Tz))+(2*size(Tr))+(Nz*Nr)+1
allocate(IGiter(Nz*Nr), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate IGiter(Nz*Nr), in boundaries1 module ***"
end if
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
dtn = dt
ct = 1
sumdt = 0.0_dp
do while (sumdt < tp)
ct = ct + 1
!Pardiso vs Lapack
if (ParTLapF) then
if (ct > 2) then
IGiter = Psfr(:,(ct-1))
end if
call Iterative_Solver_FGMRESwILU0 ((Nz*Nr),((2*size(Tz))+(2*size(Tr))+(Nz*Nr)),innzelef,colnzelef,nzelef,RHSnn,IGiter)
else
call GBSV(BTMnni, RHSnn, Nz, IPIV, INFO) !LAPACK SOLVER FOR BANDED MATRIX SYSTEM OF EQUATIONS
end if
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
deallocate(Psfr, STAT = DeAllocateStatus)
allocate(Psfr((Nz*Nr),ct), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single flow pressure vector during solver while loop, if N-N ***"
Psfr(:,ct) = RHSnn(:,1)
do i = 1,(ct-1)
Psfr(:,i) = Psfrtemp(:,i)
end do
deallocate(Psfrtemp, STAT = DeAllocateStatus)
allocate(Psfrtemp((Nz*Nr),ct), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single flow pressure vector during solver while loop, if N-N ***"
Psfrtemp = Psfr
do i = 1,(Nz*Nr)
DeltaP(i) = abs(Psfr(i,ct) - Psfr(i,(ct-1)))
end do
DPMAX = maxval(DeltaP)
if (DPMAX <= MULT*DPLIM) then
sumdt = sumdt + dtn
dtn = dtn*(DPLIM/DPMAX)
if ((sumdt+dtn > tp) .AND. (sumdt /= tp)) then
dtn = tp - sumdt
end if
BMnn = 0.0_dp !initializing Cij*Vij Matrix to zeros
do h = 1,(Nz*Nr)
BMnn(h,h) = ((1.0_dp)/(dtn))*B(h) !initializing diagonal of Cij*Vij Matrix AS IF no Wellbore Storage is considered
end do
if (ws == 0) then
BMnn = BMnn !keeping CijVij Matrix as if no wellbore storage, because wellbore storage indicator is disabled (ws = 0)
else if (ws == 1) then
do i = 1,Nz
if ((dzgp(i) < (czp-(dzp/2.0_dp))) .OR. (dzgp(i) > (czp+(dzp/2.0_dp)))) then
WSv(i) = 0.0_dp
else
if (i == 1) then
WSv(i) = (C*(dztr(1)-dzgp(1)))/(dzp)
else if (i == Nz) then
WSv(i) = (C*(dzgp(Nz)-dztr(Nz-1)))/(dzp)
else
WSv(i) = (C*(dztr(i)-dztr(i-1)))/(dzp)
end if
end if
end do
do i = 1,Nz
BMnn(i,i) = ((B(i)) + (WSv(i)))/(dtn) !modifying elements 1 to Nz (grid blocks right next to the well) of Cij*Vij Matrix
end do
end if
ATMnn = TMnn + BMnn
if (ParTLapF == .false.) then
BTMnn = 0.0_dp
do j = 1,(Nz*Nr)
do i = max(1,(j-Nz)),min((Nz*Nr),(j+Nz))
BTMnn((Nz+Nz+1+i-j),j) = ATMnn(i,j)
end do
end do
BTMnni = BTMnn
end if
RHSnn(:,1) = matmul(BMnn,Psfr(:,ct)) - NNSSV
if (ParTLapF) then
do i = 1,(Nz*Nr)
nzelef(innzelef(i)) = MDnn(i) + BMnn(i,i)
end do
end if
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
else
do while (DPMAX > MULT*DPLIM)
dtn = dtn*(DPLIM/DPMAX)
BMnn = 0.0_dp !initializing Cij*Vij Matrix to zeros
do h = 1,(Nz*Nr)
BMnn(h,h) = ((1.0_dp)/(dtn))*B(h) !initializing diagonal of Cij*Vij Matrix AS IF no Wellbore Storage is considered
end do
if (ws == 0) then
BMnn = BMnn !keeping CijVij Matrix as if no wellbore storage, because wellbore storage indicator is disabled (ws = 0)
else if (ws == 1) then
do i = 1,Nz
if ((dzgp(i) < (czp-(dzp/2.0_dp))) .OR. (dzgp(i) > (czp+(dzp/2.0_dp)))) then
WSv(i) = 0.0_dp
else
if (i == 1) then
WSv(i) = (C*(dztr(1)-dzgp(1)))/(dzp)
else if (i == Nz) then
WSv(i) = (C*(dzgp(Nz)-dztr(Nz-1)))/(dzp)
else
WSv(i) = (C*(dztr(i)-dztr(i-1)))/(dzp)
end if
end if
end do
do i = 1,Nz
BMnn(i,i) = ((B(i)) + (WSv(i)))/(dtn) !modifying elements 1 to Nz (grid blocks right next to the well) of Cij*Vij Matrix
end do
end if
ATMnn = TMnn + BMnn
if (ParTLapF == .false.) then
BTMnn = 0.0_dp
do j = 1,(Nz*Nr)
do i = max(1,(j-Nz)),min((Nz*Nr),(j+Nz))
BTMnn((Nz+Nz+1+i-j),j) = ATMnn(i,j)
end do
end do
BTMnni = BTMnn
end if
RHSnn(:,1) = matmul(BMnn,Psfr(:,ct-1)) - NNSSV
if (ParTLapF) then
do i = 1,(Nz*Nr)
nzelef(innzelef(i)) = MDnn(i) + BMnn(i,i)
end do
! IGiter(1:size(IGiter)) = Psfr(:,(ct-1))
call Iterative_Solver_FGMRESwILU0 ((Nz*Nr),((2*size(Tz))+(2*size(Tr))+(Nz*Nr)),innzelef,colnzelef,nzelef,RHSnn,IGiter)
else
call GBSV(BTMnni, RHSnn, Nz, IPIV, INFO)
end if
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
deallocate(Psfr, STAT = DeAllocateStatus)
allocate(Psfr((Nz*Nr),ct), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single flow pressure vector during solver while loop, if N-N ***"
Psfr(:,ct) = RHSnn(:,1)
do i = 1,(ct-1)
Psfr(:,i) = Psfrtemp(:,i)
end do
deallocate(Psfrtemp, STAT = DeAllocateStatus)
allocate(Psfrtemp((Nz*Nr),ct), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single flow pressure vector during solver while loop, if N-N ***"
Psfrtemp = Psfr
do i = 1,(Nz*Nr)
DeltaP(i) = abs(Psfr(i,ct) - Psfr(i,(ct-1))) !SHOULD BE ct-1!!!!
end do
DPMAX = maxval(DeltaP)
end do
sumdt = sumdt + dtn
dtn = dtn*(DPLIM/DPMAX)
if ((sumdt+dtn > tp) .AND. (sumdt /= tp)) then
dtn = tp - sumdt
end if
BMnn = 0.0_dp !initializing Cij*Vij Matrix to zeros
do h = 1,(Nz*Nr)
BMnn(h,h) = ((1.0_dp)/(dtn))*B(h) !initializing diagonal of Cij*Vij Matrix AS IF no Wellbore Storage is considered
end do
if (ws == 0) then
BMnn = BMnn !keeping CijVij Matrix as if no wellbore storage, because wellbore storage indicator is disabled (ws = 0)
else if (ws == 1) then
do i = 1,Nz
if ((dzgp(i) < (czp-(dzp/2.0_dp))) .OR. (dzgp(i) > (czp+(dzp/2.0_dp)))) then
WSv(i) = 0.0_dp
else
if (i == 1) then
WSv(i) = (C*(dztr(1)-dzgp(1)))/(dzp)
else if (i == Nz) then
WSv(i) = (C*(dzgp(Nz)-dztr(Nz-1)))/(dzp)
else
WSv(i) = (C*(dztr(i)-dztr(i-1)))/(dzp)
end if
end if
end do
do i = 1,Nz
BMnn(i,i) = ((B(i)) + (WSv(i)))/(dtn) !modifying elements 1 to Nz (grid blocks right next to the well) of Cij*Vij Matrix
end do
end if
ATMnn = TMnn + BMnn
if (ParTLapF == .false.) then
BTMnn = 0.0_dp
do j = 1,(Nz*Nr)
do i = max(1,(j-Nz)),min((Nz*Nr),(j+Nz))
BTMnn((Nz+Nz+1+i-j),j) = ATMnn(i,j)
end do
end do
BTMnni = BTMnn
end if
RHSnn(:,1) = matmul(BMnn,Psfr(:,ct)) - NNSSV
if (ParTLapF) then
! do i = 1,(Nz*Nr)
! nzele(innzele(i)) = MDnn(i) + BMnn(i,i)
! end do
do i = 1,(Nz*Nr)
nzelef(innzelef(i)) = MDnn(i) + BMnn(i,i)
end do
end if
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
end if
deallocate(tv, STAT = DeAllocateStatus)
allocate(tv(ct), STAT = AllocateStatus)
if (AllocateStatus /=0 ) STOP "*** Not enough memory to allocate single flow rate time vector during solver while loop, if N-N ***"
tv(ct) = sumdt
do i = 1,(ct-1)
tv(i) = tvtemp(i)
end do
deallocate(tvtemp, STAT = DeAllocateStatus)
allocate(tvtemp(ct), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate single flow rate temporal time vector during solver while loop, if N-N ***"
tvtemp = tv
print *, sumdt, 'sec of ', tp, 'sec'
print *, Psfr(idx2,ct)*Pa2psi, 'psi', ' at center of packer'
end do
tv(1) = 0.0_dp
end subroutine subrboundaries
!FGMRES with ILU0 Preconditioning Iterative Solver Subroutine
subroutine Iterative_Solver_FGMRESwILU0 (Nf, SJAf, IAf, JAf, Af, RHSf, COMPUTED_SOLUTIONf) !COMPUTED_SOLUTION: input = initial guess & output = computed solution
implicit none
integer,parameter :: dp=kind(1.0d0)
integer :: Nf, SJAf !Parameter
integer,parameter :: SIZEf = 128
integer,dimension(:) :: IAf !Size: (Nf+1)
integer,dimension(:) :: JAf !Size: size(JAf)
real(dp),dimension(:) :: Af !Size: size(JAf)
real(dp),dimension(:),allocatable :: BILU0f !Size: size(JAf)
real(dp),dimension(:),allocatable :: TRVECf !Size: Nf. Is computed here everytime the subroutine is called?
integer,dimension(SIZEf) :: IPARf !Is computed here everytime the subroutine is called?
integer :: IERRf
real(dp),dimension(SIZEf) :: DPARf !Is computed here everytime the subroutine is called?
real(dp),dimension(:),allocatable :: TMPf !Size: (Nf*(2*Nf+1)+(Nf*(Nf+9))/2+1). Is computed here everytime the subroutine is called?
real(dp),dimension(:),allocatable :: Bf, RESIDUALf !Size: Nf
real(dp),dimension(:,:) :: RHSf !Size: Nf
real(dp),dimension(:) :: COMPUTED_SOLUTIONf !Size: Nf
integer :: ITERCOUNTf, RCI_REQUESTf, Iff
real(dp) :: DVARf
real(dp),external :: DNRM2
real(dp),parameter :: eunrmlim = 1.0E-20 !Used in RCI_REQUEST 2
real(dp),parameter :: nrmrouce = 1.0D-20 !Used in RCI_REQUEST 4
!SOLVER
allocate(BILU0f(SJAf), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate BILU0f(SJAf) @ boundaries1 module ***"
allocate(TRVECf(Nf), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate TRVECf(Nf) @ boundaries1 module ***"
allocate(TMPf(Nf*(2*min(150,Nf)+1)+(min(150,Nf)*(min(150,Nf)+9))/2+1), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate TMPf(Nf*(2*min(150,Nf)+1)+(min(150,Nf)*(min(150,Nf)+9))/2+1) @ boundaries1 module ***"
allocate(Bf(Nf), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate Bf(Nf) @ boundaries1 module ***"
allocate(RESIDUALf(Nf), STAT = AllocateStatus)
if (AllocateStatus /= 0) STOP "*** Not enough memory to allocate RESIDUALf(Nf) @ boundaries1 module ***"
!---------------------------------------------------------------------------
! Save the right-hand side in vector Bf for future use
!---------------------------------------------------------------------------
CALL DCOPY(Nf, RHSf, 1, Bf, 1)
!---------------------------------------------------------------------------
! Initialize the solver
!---------------------------------------------------------------------------
CALL DFGMRES_INIT(Nf, COMPUTED_SOLUTIONf, RHSf, RCI_REQUESTf, IPARf, DPARf, TMPf)
IF (RCI_REQUESTf.NE.0) GOTO 999
!---------------------------------------------------------------------------
! Calculate ILU0 preconditioner.
! !ATTENTION!
! DCSRILU0 routine uses some IPAR, DPAR set by DFGMRES_INIT routine.
! Important for DCSRILU0 default entries set by DFGMRES_INIT are
! ipar(2) = 6 - output of error messages to the screen,
! ipar(6) = 1 - allow output of error messages,
! ipar(31)= 0 - abort DCSRILU0 calculations if routine meets zero diagonal element.
!
! If ILU0 is going to be used out of MKL FGMRES context, than the values
! of ipar(2), ipar(6), ipar(31), dpar(31), and dpar(32) should be user
! provided before the DCSRILU0 routine call.
!
! In this example, specific for DCSRILU0 entries are set in turn:
! ipar(31)= 1 - change small diagonal value to that given by dpar(32),
! dpar(31)= 1.D-20 instead of the default value set by DFGMRES_INIT.
! It is a small value to compare a diagonal entry with it.
! dpar(32)= 1.D-16 instead of the default value set by DFGMRES_INIT.
! It is the target value of the diagonal value if it is
! small as compared to dpar(31) and the routine should change
! it rather than abort DCSRILU0 calculations.
!---------------------------------------------------------------------------
IPARf(31)=1
DPARf(31)=1.D-20
DPARf(32)=1.D-16 !it was in 1.D-16
CALL DCSRILU0(Nf, Af, IAf, JAf, BILU0f, IPARf, DPARf, IERRf)
IF(IERRf.ne.0) THEN
PRINT *, 'Error after calculation of the',' preconditioner DCSRILU0',IERRf
PRINT *, 'Unfortunately, FGMRES+ILU0 Fortran example',' has FAILED',' during the preconditioning of the matrix'
END IF
!---------------------------------------------------------------------------
! Set the desired parameters:
! IPAR(15) = 2: do the restart after 2 iterations
! LOGICAL parameters:
! IPAR(8) = 0: do not do the stopping test for the maximal number of iterations
! IPARf(11) = 1: do the Preconditioned iterations of FGMRES method
! Set parameter IPAR(11) for preconditioner call. For this example,
! it reduces the number of iterations.
! DOUBLE PRECISION parameters
! DPAR(1) = 1.0D-3: set the relative tolerance to 1.0D-3 instead of default value 1.0D-6
! NOTE. Preconditioner may increase the number of iterations for an
! arbitrary case of the system and initial guess and even ruin the
! convergence. It is user's responsibility to use a suitable preconditioner
! and to apply it skillfully.
!---------------------------------------------------------------------------
IPARf(5) = 20 !min(150,Nf) !specifies the maximum number of iterations. The default value is min (150,n).
! IPARf(15)=1 ! specifies number of non-restarted FGMRES iterations (it was in 2)
! IPARf(5)=1000 ! specifies the maximum number of iterations - default value is min(150,Nf)
IPARf(8)=0 ! 0 = no stopping test for the maximal number of iterations (ipar(5) = min(150,n)). 1 = perform stopping test for maximal number of iterations (it was in 0)
IPARf(9)=0 ! 0 = no residual stopping test performed. 1 = residual stopping test performed (dpar(5) <= dpar(4)) (it was in 0)
IPARf(10)=1 ! 0 = not performing the user-defined stopping test. 1 = performing the user-defined stopping test (it was in 1) AT LEAST ONE OF THE PARAM ipar(8)-ipar(10) MUST BE SET TO 1.
IPARf(11)=1 ! 0 = non-preconditioned version of the FGMRES method. 1 = preconditioned version of the FGMRES method (it was in 1)
IPARf(12)=1 ! 0 = zero norm check by RCI_REQUES=4. 1 = automatic zero-norm check of the currently generated vector (dpar(7) <= dpar(8), where dpar(8) contains tolerance value) (it was in 0)
DPARf(1)=1.0D-3 ! specifies the relative tolerance - default value is 1.0D-6 (it was in 1.0D-3)
DPARf(2)=5.0D-1 ! specifies the absolute tolerance - default value is 0.0D-0
!---------------------------------------------------------------------------
! Check the correctness and consistency of the newly set parameters
!---------------------------------------------------------------------------
CALL DFGMRES_CHECK(Nf, COMPUTED_SOLUTIONf, RHSf, RCI_REQUESTf, IPARf, DPARf, TMPf)
IF (RCI_REQUESTf.NE.0) GOTO 999
!---------------------------------------------------------------------------
! Compute the solution by RCI (P)FGMRES solver with preconditioning
! Reverse Communication starts here
!---------------------------------------------------------------------------
1 CALL DFGMRES(Nf, COMPUTED_SOLUTIONf, RHSf, RCI_REQUESTf, IPARf, DPARf, TMPf)
!---------------------------------------------------------------------------
! If RCI_REQUEST=0, then the solution was found with the required precision
!---------------------------------------------------------------------------
IF (RCI_REQUESTf.EQ.0) GOTO 3
!---------------------------------------------------------------------------
! If RCI_REQUEST=1, then compute the vector A*TMP(IPAR(22))
! and put the result in vector TMP(IPAR(23))
!---------------------------------------------------------------------------
IF (RCI_REQUESTf.EQ.1) THEN
CALL MKL_DCSRGEMV('N',Nf, Af, IAf, JAf, TMPf(IPARf(22)), TMPf(IPARf(23)))
GOTO 1
END IF
!---------------------------------------------------------------------------
! If RCI_request=2, then do the user-defined stopping test
! The residual stopping test for the computed solution is performed here
!---------------------------------------------------------------------------
! NOTE: from this point vector B(N) is no longer containing the right-hand
! side of the problem! It contains the current FGMRES approximation to the
! solution. If you need to keep the right-hand side, save it in some other
! vector before the call to DFGMRES routine. Here we saved it in vector
! RHS(N). The vector B is used instead of RHS to preserve the original
! right-hand side of the problem and guarantee the proper restart of FGMRES
! method. Vector B will be altered when computing the residual stopping
! criterion!
!---------------------------------------------------------------------------
IF (RCI_REQUESTf.EQ.2) THEN
! Request to the DFGMRES_GET routine to put the solution into B(N) via IPAR(13)
IPARf(13)=1
! Get the current FGMRES solution in the vector Bf(N)
CALL DFGMRES_GET(Nf, COMPUTED_SOLUTIONf, Bf, RCI_REQUESTf, IPARf, DPARf, TMPf, ITERCOUNTf)
! Compute the current true residual via MKL (Sparse) BLAS routines
CALL MKL_DCSRGEMV('N', Nf, Af, IAf, JAf, Bf, RESIDUALf) !matrix-vector product of a sparse general matrix stored in the CSR format with one-based indexing
CALL DAXPY(Nf, -1.0D0, RHSf, 1, RESIDUALf, 1) !vector-scalar product and add the result to the original vector
DVARf=DNRM2(Nf, RESIDUALf, 1) !euclidean norm of a vector
IF (DVARf.LT.eunrmlim) THEN
GOTO 3
ELSE
GOTO 1
END IF
END IF
!---------------------------------------------------------------------------
! If RCI_REQUEST=3, then apply the preconditioner on the vector
! TMP(IPAR(22)) and put the result in vector TMP(IPAR(23))
! Here is the recommended usage of the result produced by ILU0 routine
! via standard MKL Sparse Blas solver routine mkl_dcsrtrsv.
!---------------------------------------------------------------------------
IF (RCI_REQUESTf.EQ.3) THEN
CALL MKL_DCSRTRSV('L','N','U',Nf,BILU0f,IAf,JAf,TMPf(IPARf(22)),TRVECf)
CALL MKL_DCSRTRSV('U','N','N',Nf,BILU0f,IAf,JAf,TRVECf,TMPf(IPARf(23)))
GOTO 1
END IF
!---------------------------------------------------------------------------
! If RCI_REQUEST=4, then check if the norm of the next generated vector is
! not zero up to rounding and computational errors. The norm is contained
! in DPAR(7) parameter
!---------------------------------------------------------------------------
IF (RCI_REQUESTf.EQ.4) THEN
IF (DPARf(7).LT.nrmrouce) THEN
GOTO 3
ELSE
GOTO 1
ENDIF
!---------------------------------------------------------------------------
! If RCI_REQUEST=anything else, then DFGMRES subroutine failed
! to compute the solution vector: COMPUTED_SOLUTION(N)
!---------------------------------------------------------------------------
ELSE
GOTO 999
END IF
!---------------------------------------------------------------------------
! Reverse Communication ends here
! Get the current iteration number and the FGMRES solution. (DO NOT FORGET to
! call DFGMRES_GET routine as computed_solution is still containing
! the initial guess!). Request to DFGMRES_GET to put the solution into
! vector COMPUTED_SOLUTION(N) via IPAR(13)
!---------------------------------------------------------------------------
3 IPARf(13)=1 !if 1 solution is in RHSf vector. if 0 solution is in COMPUTED_SOLUTIONf vector
CALL DFGMRES_GET(Nf, COMPUTED_SOLUTIONf, RHSf, RCI_REQUESTf, IPARf, DPARf, TMPf, ITERCOUNTf)
!---------------------------------------------------------------------------
! Print solution vector: COMPUTED_SOLUTION(N) and
! the number of iterations: ITERCOUNT
!---------------------------------------------------------------------------
PRINT *, 'The system has been solved'
! PRINT *, 'The following solution has been obtained:'
! DO Iff=1,N
! PRINT *, 'COMPUTED_SOLUTION(',Iff,')=',COMPUTED_SOLUTION(Iff)*0.00014503773773021 !format '(A18,I1,A2,E10.3)'
! END DO
PRINT *, 'Number of iterations: ',ITERCOUNTf
!---------------------------------------------------------------------------
! Release internal MKL memory that might be used for computations
! NOTE: It is important to call the routine below to avoid memory leaks
! unless you disable MKL Memory Manager
!---------------------------------------------------------------------------
CALL MKL_FREEBUFFERS
999 PRINT *, 'The solver has returned the ERROR code ',RCI_REQUESTf
CALL MKL_FREEBUFFERS
end subroutine Iterative_Solver_FGMRESwILU0
end module mboundaries
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page