Different matrix multiplication results between C and Matlab.

[Anas_A_]

Let covold be a matrix of size 72x72, theta be a vector of size 1x72 and meanold a vector of size 1x72. I want to compute

[(w-1)/w ]* covold + [ 1/(1+w) ] * (theta - meanold)' * (theta  - meanold)

where w=144.0.

I wrote a code in C and a code in Matlab in order to compare the results. I noticed that the results are different. For example the variance of the first variable is:

C: 0.001890

Matlab: 0.003690258

I would like to ask if this is normal. I attach the data and the results using Matlab (matlabcov.txt).

Thank you very much.
 

The code in C is:

#include "stdafx.h"
#include <math.h>               /* Math stuff      ISOC  */
#include <stdio.h>              /* I/O lib         ISOC  */
#include <stdlib.h>             /* Standard Lib    ISOC  */
#include <fstream>
#include <mkl.h>
#include <conio.h>
#include <iostream>
#include <string>

using namespace std;

void fReadMtrx(string f, double *mtrx, int nrow, int ncol);

#define NPARS 72
#define N 144

int main()
{    
    int i, j, info, dimen = NPARS;
    double meanold[NPARS], covold[NPARS*NPARS], subvec[NPARS], theta[NPARS];

    double weight = 144.0;

    fReadMtrx("MEAN.txt", meanold, NPARS, 1);
    fReadMtrx("thetacan.txt", theta, NPARS, 1);
    fReadMtrx("COVFILE.txt", covold, NPARS, NPARS);

    /*Update Covariance and Mean */
    vdSub(NPARS, theta, meanold, subvec );

            
    cblas_dgemm(CblasRowMajor, CblasTrans, CblasNoTrans, NPARS, NPARS, 1, 1.0/(1.0+weight), subvec,
        NPARS,  subvec,  NPARS, (weight-1.0)/weight, covold, NPARS);

    for(i=0; i<NPARS; i++){
        for(j=0; j<NPARS; j++){
            printf("%lf \t", covold[i*NPARS+j]);
        }
        printf("%lf \n \n");
    }

return 0;
}

void fReadMtrx(string f, double *mtrx, int nrow, int ncol)
{
  ifstream data(f.c_str(), ios::in);
  if (!data) {
    cerr << "File " << f << " could not be opened." << endl;
    exit(1);
  }
  for(int i = 0; i < nrow; i++)
    for(int j = 0; j < ncol; j++)
      data >> mtrx[i*ncol+j];
} // end of function fReadMtrx

//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

The node in Matlab:

covold=load('COVFILE.txt');
meanold=load('MEAN.txt');
theta=load('thetacan.txt')';

 weightold = 144; npars=72;
 
 % Recursive form of covariance matrix
 covold= ((weightold-1)/weightold)*covold + ...
     (1/(1+weightold))* ((theta - meanold)*(theta-meanold)');
 
 fcov = fopen('matlabcov.txt', 'wt');
 for i=1:npars
     for j =1:npars
         fprintf(fcov, '%0.9f \t', covold(i,j));
     end
     fprintf(fcov,'\n');
 end
 
 fclose(fcov);

[Andrey_N_Intel]

Hi Anas,

I wonder if you evaluated algorithms for covariance matrix computation available in Statistical component of Intel MKL and compared their output against Matlab? In MKL we support several methods for computation of covariance/correlation. Fast and single pass methods are among them. The library also allows re-using the mean estimate obtained earlier instead of its computation during evaluation of covariance - "user mean" method supports this use model.

Thanks,

Andrey

[Anas_A_]

Hi Andrey! Thanks for the help.

The first time I computed the covariance matrix and the mean the results between Matlab and C were similar. I wanted to compute the covariance matrix and the mean sequentially but I didn't know how to do that with MKL so I tried to compute it by myself. Also do you know if MKL has a routine to force the covariance matrix to me positive define? I think I could do that with the routine of the robust covariance matrix but the first time I compute the covariance matrix the data are 144 and the parameters 72.

[Andrey_N_Intel]

Hi Anas,

Can you please clarify what you mean by computation of the covariance matrix and the mean sequentially? Does it mean that you compute the average first, and compute the covariance after that, and computation of the covariance relies on the pre-computed mean (in other terms, you need two pass approach for computation of the covariance matrix)?

Answering your second question - yes, In Statistical component of Intel MKL we provide the algorithm for stabilization of the correlation matrix. The input to the algorithm is the symmetric matrix which is not positively definite, and the output is the matrix which is "close" to the original and is positively semi-defined. The method VSL_SS_METHOD_SD, spectral decomposition method for parameterization of a correlation matrix is responsible for this type of the computations. Please, see additional details in Summary Stats application notes, http://software.intel.com/en-us/node/497944

Thanks, Andrey

[Anas_A_]

By saying sequentially I mean:

for t =145 :T

I have available t-1 observations and I need to simulate from a d-dimensional Normal distribution with mean the vector theta and variance covariance matrix the current empirical estimate of  the covariance matrix.

end

Each time  I add a new  observation so, instead of estimate each time the covariance matrix from the beginning I use a recursive formula for the covariance matrix. As you said I compute the mean first, and compute the covariance after that, and computation of the covariance relies on the pre-computed mean.

Thank you very much.

[Andrey_N_Intel]

Hi Anas,

MKL covariance algorithm supports the streaming way of the processing; that is, when the data comes in blocks the covariance algorithm can update the estimate using it previous value and the latest observation data. Please, have a look at the section "Processing Data in Blocks" in Summary Stats Application notes, http://software.intel.com/en-us/node/497946

Computational flow is mostly the same as in case of the processing of the whole dataset, but you need additionally to initialize covariance matrix with zeros (or other meaningful for you numbers), and register in the library the array which would hold the accumulated weights.

The file vslddataprocessinginblocks.c available in examples/vslc of MKL installation tree contains the example which shows how to do progressive computation of estimates.

Please, let me know, if you need more details.

Andrey

[Anas_A_]

I didn't find the file vslddataprocessinginblocks.c but I read the notes about Summary Statistics Application. I tried to compute the covariance matrix and the mean sequentially. If I have understood right the blocks must be of the same size. So I thought to compute the covariance matrix (C) and the mean (M) of the first data and then to use the recursive form and to initialize the mean and the covariance matrix with C and the mean with M. Then I say that the blocks have size 1.

Let a be the matrix that I want to find the covariance matrix.

a =       1     4     7    10    13     1     3
            2     5     8    11    10     1     3
            3     6     9    12     4     2     2

The true covariance matrix is  

   21.2857   17.5238    9.7143
   17.5238   15.9048   11.8095
    9.7143   11.8095   14.6190

and the true mean is

    5.5714    5.7143    5.4286

( I found it with Matlab.)

I computed the covariance matrix and the mean of the first 4 data. So as initial covariance matrix I chose    

    15    15    15
    15    15    15
    15    15    15

and initial mean

    5.5000    6.5000    7.5000.

The result I got is wrong. I would like to ask you if you could help me to understand what I have done wrong.

Thank you very much.

The C code is:

#include <stdio.h>              /* I/O lib         ISOC  */
#include <mkl.h>

#define DIM 3 /* Task dimension */
#define N 1 /* Number of observations */
#define NBLOCK 4 /* Number of blocks */

int main()
{
    VSLSSTaskPtr task; /* SS task descriptor */

    int  i, j;

    double x[DIM]={13, 10, 4}; /* Array for dataset */

    double W[2]; /* Array of accumulated weights */
    MKL_INT p, n, xstorage = VSL_SS_MATRIX_STORAGE_ROWS; ;
    MKL_INT covstorage = VSL_SS_MATRIX_STORAGE_FULL;

    int status, block_idx;

    /* Initialize variables used in the computation of mean */
    p = DIM; n = N;
    double mean[3] = {5.5 ,6.5 ,7.5};
    double cov[DIM*DIM] = {15, 15, 15, 15, 15, 15, 15, 15, 15};       

    W[0] = 4.0; W[1] = 16.0;

    /* Create task */
    status = vsldSSNewTask( &task, &p, &n, &xstorage, x, 0, 0 );
    status = vsldSSEditCovCor( task, mean, cov, &covstorage, 0, 0 );

    /* Initialize task parameters */
   // status = vsldSSEditTask( task, VSL_SS_ED_MEAN, &mean );
    status = vsldSSEditTask( task, VSL_SS_ED_ACCUM_WEIGHT, W );

    double theta[6]={1,1,2,3,3,2};

    /* Compute the mean estimate for block-based data using SS one-pass method */
    for( block_idx = 1;  block_idx<=NBLOCK; block_idx++)
   {
          status = vsldSSCompute( task, VSL_SS_COV, VSL_SS_METHOD_1PASS );
   
          //GetNextDataBlock( x, N );

          for( i=0; i<3; i++){
              x = theta[i + block_idx - 1];

       }
 

    }
   
   printf(" covariance estimate:\n");
   for ( i = 0; i < p; i++ ){
       for( j = 0; j < p; j++ ) printf("%lf \t", cov[i*p+j]);
       printf("\n");
   }

   printf(" mean estimate:\n");
   for ( i = 0; i < p; i++ ) {
       printf("%lf \n", mean);
   }

    /* De-allocate task resources */
     status = vslSSDeleteTask( &task );
     return 0;
   }

[Andrey_N_Intel]

Hi Anas,

I made several modifications in your example. Among them

- number of blocks is set ot 3 as you process three additional blocks

- both elements in the array W are set to 4 as you do not assign weights to observation vectors what means that each vector is assigned weight 1, by default; this means that accumulated weights/squares of weights are both equal to 4.

-  modified copy loop as shown  x = theta[i + DIM*block_idx]; and re-worked the major computation loop.

Please, have a look.

#include <stdio.h>              /* I/O lib         ISOC  */
#include <mkl.h>

#define DIM 3 /* Task dimension */
#define N 1 /* Number of observations */
#define NBLOCK 3 /* Number of blocks */

int main()
 {
     VSLSSTaskPtr task; /* SS task descriptor */

    int  i, j;

    double x[DIM]; /* Array for dataset */

    double W[2]; /* Array of accumulated weights */
     MKL_INT p, n, xstorage = VSL_SS_MATRIX_STORAGE_ROWS; ;
     MKL_INT covstorage = VSL_SS_MATRIX_STORAGE_FULL;

    int status, block_idx;

    /* Initialize variables used in the computation of mean */
     p = DIM; n = N;
     double mean[3] = {5.5 ,6.5 ,7.5};
     double cov[DIM*DIM] = {15.0, 15.0, 15.0, 15.0, 15.0, 15.0, 15.0, 15.0, 15.0};

    W[0] = 4.0; W[1] = 4.0;

    /* Create task */
     status = vsldSSNewTask( &task, &p, &n, &xstorage, x, 0, 0 );
     status = vsldSSEditCovCor( task, mean, cov, &covstorage, 0, 0 );

    /* Initialize task parameters */
    // status = vsldSSEditTask( task, VSL_SS_ED_MEAN, &mean );
     status = vsldSSEditTask( task, VSL_SS_ED_ACCUM_WEIGHT, W );

    double theta[]={13.0,10.0,4.0,1.0,1.0,2.0,3.0,3.0,2.0};

    /* Compute the mean estimate for block-based data using SS one-pass method */
     for( block_idx = 0;  block_idx<NBLOCK; block_idx++)
    {
        for( i=0; i<DIM; i++)
  {
             x = theta[i + DIM*block_idx];
        }
        status = vsldSSCompute( task, VSL_SS_COV, VSL_SS_METHOD_1PASS );
    }

    printf(" covariance estimate:\n");
    for ( i = 0; i < p; i++ ){
        for( j = 0; j < p; j++ ) printf("%lf \t", cov[i*p+j]);
        printf("\n");
    }

   printf(" mean estimate:\n");
    for ( i = 0; i < p; i++ ) {
        printf("%lf \n", mean);
    }

    /* De-allocate task resources */
      status = vslSSDeleteTask( &task );
      return 0;
}

The library allows you to avoid copy operation, and you just need to register the address of the next vector (block) in the library as shown below

for( block_idx = 0; block_idx<NBLOCK; block_idx++)
{
    status = vsldSSEditTask( task, VSL_SS_ED_OBSERV, theta+block_idx*DIM );
    status = vsldSSCompute( task, VSL_SS_COV, VSL_SS_METHOD_1PASS );
}

Generally, the library does not require you to provide the blocks of the equal size on each iteration. You just need to register the address of the next block in the library using the proper editor as one above (or just copy the data to the same address given the array has sufficient room to store the data) and properly modify number of observations.

Please, let me know if you have more questions.

Andrey

[Anas_A_]

Hi Andrey!

Thank you very much for your help. Can I use this routine with the Robust Estimation of Covariance Matrix/ Mean? And if I do I replace this
 

status = vsldSSEditCovCor( task, mean, cov, &covstorage, 0, 0 );

status = vsldSSCompute( task, VSL_SS_COV, VSL_SS_METHOD_1PASS );

with this

status = vsldSSEditRobustCovariance( task, &covstorage, &nparams, params, mean, cov );

status = vsldSSCompute( task, VSL_SS_ROBUST_COV, VSL_SS_METHOD_TBS );

I ask you this because sometimes the covariance matrix is not positive define and the Cholesky decomposition fails. I read how to Parametrize a Correlation Matrix  ( http://software.intel.com/en-us/node/497944 ) but it is about the correlation matrix.

Thanks again for the help.

[Andrey_N_Intel · Accepted solution]

Hi Anas,

Current version of Intel MKL robust covariance estimator does not support streaming mode.

I just wonder if you investigated the reasons of why your covariance matrix fails the Cholesky decomposition? Do you work with the real data which may result in (tiny) negative eigenvalue of the covariance matrix? If so, what is output of the MKL Lapack pstf2 routine which does Cholesky decomposition with the full pivoting? If the issue is related to numerical aspects, would use of more robust decomposition such as SVD help?  Another thought is to investigate presence of the outliers in your dataset. Have you run MKL Summary Stats algorithm for detection of outliers?

Thanks, Andrey

[Anas_A_]

Hi Andrey. I followed your suggestions and I found out that the covariance matrix is symmetric but has negative eigenvalues. The problem I face is:

I want to simulate from a multivariate normal distribution. When I try to do it with Matlab everything works. Matlab uses the function cholcov to factorize the covariance matrix. The description of this function is:

function [T,p] = cholcov(Sigma,flag)
%CHOLCOV  Cholesky-like decomposition for covariance matrix.
%   If SIGMA is not positive definite, T is computed from an eigenvalue
%   decomposition of SIGMA.  T is not necessarily triangular or square in
%   this case.  Any eigenvectors whose corresponding eigenvalue is close to
%   zero (within a small tolerance) are omitted.  If any remaining
%   eigenvalues are negative, T is empty.

I wrote a similar code in C but the factorization still fails. I tested my code with a small matrix and it is correct. I noticed that the eigenvectors/eigenvalues are different and so I think this is the reason.  For example the first 5 elements of the first row using Matlab is:

-0.178640536933692  -0.171785233742083   0.003536032250076   0.215976356770781   0.047220738084061

and using the function LAPACKE_dsyev( LAPACK_ROW_MAJOR, 'V', 'U', n, a, lda, w ); is:

-0.128768     -0.028550     0.101975     -0.159201     -0.099586 .

The first five eigenvalues with C is -0.000004     -0.000004     -0.000004     -0.000004     -0.000003

and with Matlab

   1.0e-12 *

  -0.286064537835538  -0.254355758173010  -0.227684048920343  -0.211110573333574  -0.126353300135388.

I would like to ask you if  I am using a wrong function to calculate the eigenvalues.

Thank you very much.

[Anas_A_]

I found why the eigenvalues are not the same. It is because the covariance matrix calculated by Matlab and my C are similar but  not identical. I would like to ask you if there is a way to find the weighted covariance matrix using this type  

I think intel  by default computes the covariance matrix divided by one minus the sum of squares of the weights.

[Andrey_N_Intel]

Hi Anas,

What is maximal absolute difference between elements of the matrices calculated in C and Matlab?

Yes, [d|s]syev function can be used to calculate eigen-values and, optionally, eigen-vectors of real symmetric matrix.

Answering your question about weighted covariance matrix: yes, Intel MKL covers this case as well. To calculate, weighted covariance matrix you need to provide array w of weights (non-negative floating-point numbers) assigned to vectors of your data matrix on the stage of the task construction: status = vsl[d|s]SSNewTask(&task, p, n, xstorage, x, w, indices);

or later, on the stage of setting parameters of the task:  status = vsldSSEditTask(task, VSL_SS_ED_WEIGHTS, w);

The library returns unbiased estimate of the covariance matrix by dividing by B=W[0] - W[1] / W[0] where W[0] = sum {w(i), i=1,...,n} and W[1]= sum { w(i) * w(i), i=1,...,n}, n is number of observation vectors. In specific case when all w(i)=1, B=n-1. I believe Matlab version of covariance algorithm also applies the same approach :"C = cov(x) or C = cov(x,y) normalizes by N – 1, if N > 1, where N is the number of observations. "

If for some reasons you need another scaling factor, you can do this by using one of approaches below:

- calculate weighted covariance matrix with MKL as described above and use the scaling factor you need: for example multiply elements of the covariance matrix by B / W[0]

- calculate cross-product matrix VSL_SS_CP with MKL 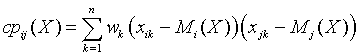  (also see "Mathematical Notation and Definitions" section in Summary Statistics Chapter in MKL Manual), and normalize it by the factor you need: for example, multiply all elements of the cross-product matrix by 1 / W[0].

Please, let me know, if you have additional questions

Andrey

[Anas_A_]

Hi Andrey!

I computed the weighted covariance matrix with the routine of MKL and the maximal absolute difference between elements of the matrices calculated in C and Matlab is 4.9964e-07.

I think that the problem is with the way I compute eigenvectors. The weighted covariance matrix is of size 72x72. When I compute the eigenvetors of the maxtrix cov(1:8, 1:8) the results are similar:

C:

LAPACKE_dsyev (row-major, high-level) Example Program Results

 Eigenvalues
 -0.000054 1.427183 10.758958 52.897686 74.362089 136.253008 194.688280 350.1769
50

 Eigenvectors (stored columnwise)
 0.515386 0.159367 -0.286849 -0.669017 0.235831 0.099866 -0.294156 -0.164305
 0.405829 0.150487 0.037140 0.077003 -0.548590 -0.441154 0.265017 -0.489435
 0.285582 0.123878 0.309648 0.362790 0.128867 0.698942 0.011544 -0.412722
 -0.046588 0.166949 -0.275717 0.392072 0.671869 -0.415776 -0.026933 -0.339432
 -0.013717 -0.799634 -0.464384 0.020837 -0.051799 0.167395 0.135810 -0.308485
 0.505743 -0.166573 0.123221 0.014151 0.321240 -0.059478 0.644899 0.422453
 0.454486 -0.335560 0.153900 0.367831 -0.062415 -0.210976 -0.637902 0.257939
 0.153075 0.359133 -0.699940 0.353858 -0.256212 0.240732 0.033498 0.328240


>>MATLAB

>> [U,D] = eig(Sigma(1:N,1:N))
U =
    0.5154    0.1594   -0.2868   -0.6690    0.2358    0.0999   -0.2942   -0.1643
    0.4058    0.1505    0.0371    0.0770   -0.5486   -0.4412    0.2650   -0.4894
    0.2856    0.1239    0.3096    0.3628    0.1289    0.6989    0.0115   -0.4127
   -0.0466    0.1670   -0.2757    0.3921    0.6719   -0.4158   -0.0269   -0.3394
   -0.0137   -0.7996   -0.4644    0.0208   -0.0518    0.1674    0.1358   -0.3085
    0.5057   -0.1666    0.1232    0.0142    0.3212   -0.0595    0.6449    0.4225
    0.4545   -0.3356    0.1539    0.3678   -0.0624   -0.2110   -0.6379    0.2579
    0.1531    0.3591   -0.6999    0.3539   -0.2562    0.2407    0.0335    0.3282
D = -0.0000    1.4272   10.7589   52.8977   74.3620  136.2530  194.6883  350.1770
>>
------------------------------------------------------------------------------------------------

When I compute the eigenvetors of the maxtrix cov(1:9, 1:9) the first two columns are not similar anymore.

LAPACKE_dsyev (row-major, high-level) Example Program Results
Weighted Covariance Matrix:

   56.3916   -5.4461   21.0892   14.2106   11.8545  -57.3334    4.1571  -32.3024   15.2373
   -5.4461  146.8146   25.6903   55.8912   51.6568  -48.5882  -60.4055  -57.3076  -16.0235
   21.0892   25.6903  135.4878   22.4742   59.0458  -61.5392  -51.8902  -22.3711  -37.1519
   14.2106   55.8912   22.4742  106.5974   25.5030  -34.2876  -11.3883  -56.1283   33.8852
   11.8545   51.6568   59.0458   25.5030   44.1879  -31.5876  -49.2822  -24.6174  -28.2669
  -57.3334  -48.5882  -61.5392  -34.2876  -31.5876  151.8341  -41.1556   43.9437  -35.8322
    4.1571  -60.4055  -51.8902  -11.3883  -49.2822  -41.1556  116.4474   25.3112   64.5246
  -32.3024  -57.3076  -22.3711  -56.1283  -24.6174   43.9437   25.3112   62.8033   -4.9204
   15.2373  -16.0235  -37.1519   33.8852  -28.2669  -35.8322   64.5246   -4.9204   84.1603

LAPACKE_dsyev (row-major, high-level) Example Program Results

 Eigenvalues:
 -0.000057 0.000023 10.019260 21.561065 54.367911 78.008325 148.580208 240.545184 351.642481

 Eigenvectors (stored columnwise)
 0.464211 0.286119 -0.253666 -0.138729 -0.688994 -0.161246 -0.197438 0.236286 -0.153382
 0.369437 0.207801 0.075771 -0.113015 0.137812 0.547265 0.479130 -0.106393 -0.492387
 0.266667 0.116239 0.350457 -0.079392 0.401792 -0.271112 -0.597882 -0.122541 -0.422891
 -0.102864 0.247021 -0.323244 0.270853 0.259084 -0.606857 0.415646 0.193232 -0.324115
 0.153243 -0.749641 -0.529701 -0.054766 0.048735 0.005765 -0.098534 -0.136057 -0.316769
 0.537240 -0.085383 0.121956 -0.028795 0.011747 -0.373801 0.306880 -0.544996 0.396636
 0.497502 -0.142657 0.019880 0.474899 0.280762 0.162971 -0.060372 0.561165 0.286842
 0.066352 0.405470 -0.608450 -0.322486 0.415615 0.164747 -0.207056 -0.103762 0.321663
 0.048082 -0.215439 0.191162 -0.744958 0.153808 -0.198146 0.225448 0.489173 0.082056


>>MATLAB

    0.0888   -0.5380   -0.2537   -0.1387   -0.6890   -0.1612   -0.1974    0.2363   -0.1534
    0.0522   -0.4206    0.0758   -0.1130    0.1378    0.5473    0.4791   -0.1064   -0.4924
    0.0065   -0.2908    0.3505   -0.0794    0.4018   -0.2711   -0.5979   -0.1225   -0.4229
    0.2676    0.0015   -0.3232    0.2709    0.2591   -0.6069    0.4156    0.1932   -0.3241
   -0.7518    0.1424   -0.5297   -0.0548    0.0487    0.0058   -0.0985   -0.1361   -0.3168
   -0.2827   -0.4648    0.1220   -0.0288    0.0117   -0.3738    0.3069   -0.5450    0.3966
   -0.3206   -0.4063    0.0199    0.4749    0.2808    0.1630   -0.0604    0.5612    0.2868
    0.3501   -0.2151   -0.6084   -0.3225    0.4156    0.1647   -0.2071   -0.1038    0.3217
   -0.2176    0.0372    0.1912   -0.7450    0.1538   -0.1981    0.2254    0.4892    0.0821

D =  -0.0000   -0.0000   10.0193   21.5611   54.3679   78.0083  148.5802  240.5452  351.6425

When I compute the eigenvetors of the maxtrix cov(1:10, 1:10) the first three columns are not similar anymore.
 

Weighted Covariance Matrix:
   56.3916   -5.4461   21.0892   14.2106   11.8545  -57.3334    4.1571  -32.3024   15.2373  -12.0170
   -5.4461  146.8146   25.6903   55.8912   51.6568  -48.5882  -60.4055  -57.3076  -16.0235   23.2106
   21.0892   25.6903  135.4878   22.4742   59.0458  -61.5392  -51.8902  -22.3711  -37.1519   18.9639
   14.2106   55.8912   22.4742  106.5974   25.5030  -34.2876  -11.3883  -56.1283   33.8852   23.7952
   11.8545   51.6568   59.0458   25.5030   44.1879  -31.5876  -49.2822  -24.6174  -28.2669    7.0779
  -57.3334  -48.5882  -61.5392  -34.2876  -31.5876  151.8341  -41.1556   43.9437  -35.8322   10.3152
    4.1571  -60.4055  -51.8902  -11.3883  -49.2822  -41.1556  116.4474   25.3112   64.5246  -18.7151
  -32.3024  -57.3076  -22.3711  -56.1283  -24.6174   43.9437   25.3112   62.8033   -4.9204  -27.0933
   15.2373  -16.0235  -37.1519   33.8852  -28.2669  -35.8322   64.5246   -4.9204   84.1603  -23.3719
  -12.0170   23.2106   18.9639   23.7952    7.0779   10.3152  -18.7151  -27.0933  -23.3719   48.1540

LAPACKE_dsyev (row-major, high-level) Example Program Results

 Eigenvalues
 -0.000074 -0.000007 0.000069 14.383856 47.663747 56.938335 81.601720 150.841004 244.580663 356.869088

 Eigenvectors (stored columnwise)
 -0.481945 0.238691 -0.296280 -0.058899 -0.224708 -0.661197 -0.103156 -0.197077 -0.250968 0.139158
 -0.286255 0.310447 -0.042790 0.117771 0.076327 0.153157 0.575001 0.442529 0.085 446 0.492887
 -0.121402 0.321346 0.153835 0.274036 0.222007 0.314981 -0.307425 -0.595861 0.091624 0.420454
 0.138479 0.147031 -0.175741 -0.457146 0.261977 0.083460 -0.565433 0.428019 -0.190057 0.323579
 -0.414390 -0.691821 0.256296 -0.343323 0.189936 -0.044647 0.049596 -0.119904 0.111411 0.314305
 -0.444848 0.216592 0.258796 0.073873 0.130422 -0.097410 -0.323642 0.299107 0.570384 -0.369756
 -0.389791 0.198062 0.340298 -0.282169 -0.207850 0.437734 0.042489 -0.017191 -0.535665 -0.299269
 -0.229001 0.004085 -0.678527 -0.201394 0.422988 0.276068 0.171912 -0.215680 0.105579 -0.322852
 -0.179141 -0.272966 -0.026355 0.632220 0.416494 -0.041068 -0.145469 0.238512 -0.479687 -0.098481
 -0.213996 -0.287199 -0.382463 0.235318 -0.614075 0.390115 -0.291176 0.139765 0.138791 0.131193

>>MATLAB

>> [U,D] = eig(Sigma(1:N,1:N))
U =
   -0.3277    0.4663   -0.2286   -0.0589   -0.2247   -0.6612   -0.1032   -0.1971   -0.2510    0.1392
   -0.0137    0.3774   -0.1938    0.1178    0.0763    0.1532    0.5750    0.4425    0.0854    0.4929
    0.2155    0.2775   -0.1350    0.2740    0.2220    0.3150   -0.3074   -0.5959    0.0916    0.4205
   -0.0207   -0.0933   -0.2501   -0.4571    0.2620    0.0835   -0.5654    0.4280   -0.1901    0.3236
   -0.2651    0.1150    0.7953   -0.3433    0.1899   -0.0446    0.0496   -0.1199    0.1114    0.3143
    0.1233    0.5371    0.0902    0.0739    0.1304   -0.0974   -0.3236    0.2991    0.5704   -0.3698
    0.2028    0.4973    0.1361   -0.2822   -0.2078    0.4377    0.0425   -0.0172   -0.5357   -0.2993
   -0.6354    0.0646   -0.3240   -0.2014    0.4230    0.2761    0.1719   -0.2157    0.1056   -0.3229
   -0.2132    0.0332    0.2464    0.6322    0.4165   -0.0411   -0.1455    0.2385   -0.4797   -0.0985
   -0.5194   -0.0149    0.0671    0.2353   -0.6141    0.3901   -0.2912    0.1398    0.1388    0.1312

D =  -0.0000   -0.0000   -0.0000   14.3839   47.6638   56.9384   81.6017  150.8410  244.5806  356.8691

The eigenvectos change when the eigenvalues are close to zero. I did some search and found that MATLAB uses LAPACK routines to compute eigenvalues and eigenvectors: If the matrix is Real Symmetric it uses the dsyev (http://nf.nci.org.au/facilities/software/Matlab/techdoc/ref/eig.html)
Isn't it strange that the results are different?

 Matlab computes eigenvectors with this way:

  [V,D] = eig(A) returns matrix V, whose columns are the right eigenvectors of A such that A*V = V*D. The eigenvectors in V are normalized so that the 2-norm of each is 1. Method: 'chol'Computes the generalized eigenvalues of A and B using the Cholesky factorization of B.

The code I used is:

/* Parameters */
#define N 9
#define LDA N

/* Main program */
int main() {

        /* Locals */
        MKL_INT n = N, lda = LDA, info;

        /* Local arrays */
        double w;
        double a[LDA*N];

        fReadMtrx("weightedcov.txt", a, N, N);


        /* Executable statements */
        printf( "LAPACKE_dsyev (row-major, high-level) Example Program Results\n" );

        /* Solve eigenproblem */
        info = LAPACKE_dsyev( LAPACK_ROW_MAJOR, 'V', 'U', n, a, lda, w );

        /* Check for convergence */
        if( info > 0 ) {
                printf( "The algorithm failed to compute eigenvalues.\n" );
                exit( 1 );
        }

        /* Print eigenvalues */
        print_matrix( "Eigenvalues", 1, n, w, 1 );

        /* Print eigenvectors */
        print_matrix( "Eigenvectors (stored columnwise)", n, n, a, lda );

        exit( 0 );
} /* End of LAPACKE_dsyev Example */

/* Auxiliary routine: printing a matrix */
void print_matrix( char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda ) {
        MKL_INT i, j;
        printf( "\n %s\n", desc );
        for( i = 0; i < m; i++ ) {
                for( j = 0; j < n; j++ ) printf( " %lf", a[i*lda+j] );
                printf( "\n" );
        }
}
void fReadMtrx(string f, double *mtrx, int nrow, int ncol)
{
  ifstream data(f.c_str(), ios::in);
  if (!data) {
    cerr << "File " << f << " could not be opened." << endl;
    exit(1);
  }
  for(int i = 0; i < nrow; i++)
    for(int j = 0; j < ncol; j++)
      data >> mtrx[i*ncol+j];
} // end of function fReadMtrx

Thank you very much for helping  me.

[Andrey_N_Intel]

Hi Anas,

per my discussion with Intel MKL Lapack team, we have few comments related to your question on eigen solver output:

- you see the different eigen-vectors that correspond to eigen-values close to zero. We can consider those eigen-values as multiple up to some tolerance. In this case you can't expect that corresponding eigen-vectors are uniquely defined: if Au = lambda u and Av = lambda v, than linear combination of u and v is the eigen-vector corresponding to the same value, A (c1 u + c2 v) = lamba (c1 u + c2 v). It defines the sensitivity of resulting eigen-vectors to floating-point errors/perturbations in the matrix.

- Thus, it does not make big sense to compare eigen-values/vectors returned by different algorithms. More reliable way to evaluate correctness of the algorithm is calculation of the quality metrics || A - U Lambda U^t || / || A || and |U^t U - I|| where A=U Lambda U^t is full eigen-decomposition of the matrix A of size n x n. Both metrics should be small ~O( n * eps ). Additional ways to evaluate correctness of the eigen-solver exist, but it makes sense to start with the one described above.

Please, let me know if this answers your question

Thanks,

Andrey

[Anas_A_]

Hi Andrey!

I appreciate your help. Thank you very much.