- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
In Section 6.1.4 of the Intel FPGA SDK for OpenCL Pro Edition: Best Practices Guide for version 20.4, the documentation covers "Relaxing Loop-Carried Dependency by Inferring Shift Registers", and uses an accumulation operation to motivate the issue.
I understand the dependency on the variable "temp_sum" that causes the initiation interval to not be 1, but instead, II=12 cycles.
What I'm uncertain of is how a shift register solves this problem? I see that there is a correlation between how big to make the shift register and how many cycles it takes for the floating point add to complete. And I understand that the shift register is used as a buffer in some way, and that it is used to remove the inter-loop dependency on "temp_sum". And I understand that in the very last loop, we need to perform a reduction on the shift register in order to get the final accumulation result. However, I am unsure of when the floating point add is scheduled and when the shifts for the shift registered are scheduled. My initial thought was that the output of a floating point add would feed the shift register, but I have been unable to convince myself of how the operation scheduling works out.
I have version 19.1 of the tools and I'm trying to use the system viewer, block viewer, and cluster viewer to try to understand when these operations are scheduled, but I am still confused.
Can someone help me understand the intuition as to why a shift register solves this problem? Perhaps someone could post the schedule in a cartoon drawing or diagram? I am not looking for a very detailed diagram. Just something to help me understand how the floating point add and shift register operations are scheduled.
Thanks!
Link Copied
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The dependency on temp_sum is a read-after-write dependency. It takes 12 cycles to perform the double-precision add in this example. Hence it takes 12 cycles to get temp_sum for each loop iteration, which means the next iteration can only read the temp_sum generated by the previous iteration after 10 cycles, resulting in an II of 12.
To solve this dependency, the read and the write operations need to be decoupled and go to different variables. This is exactly what the shift register does. If you look at line 22 in the optimized code, you will notice that the read and the write do not involve the same variable anymore. Read is now from shift_reg[0], while write is to shift_reg[12], hence the dependency is resolved. Though, in this example, the shift register size is 13; in my experience, 12 works as well.
Looking at it from above, what is happening here is that instead of having one reduction variable (temp_sum), 13 partial sum variables are introduced and every loop iteration, index 0 of the shift register is summed with a new value and written to the end of the shift register. Then the whole shift register is shifted left and the loop moves to the next iteration. Note that because the shift loop is fully unrolled, the left shift happens in one clock cycle. In iteration 0, shift_reg[0] is zero and shift_reg[12] gets the first partial sum while every other index is zero. After the shift left, both shift_reg[11] and shift_reg[12] will have the same value while every other index remains zero. In iteration 1, shift_reg[0] is still zero and shift_reg[12] is overwritten with a new partial sum. After the shift left, shift_reg[10] will have iteration 0's partial sum, while both shift_reg[11] and shift_reg[12] will have iteration 1's partial sum. This continues until 13 iterations are done and every index in the shift register has a partial sum. After that the process repeats, with the only difference being that shift_reg[0] won't be zero anymore and will have the partial sum from 13 iterations ago. After the reduction loop is complete, as you mentioned, a reduction on all the indexes of the shift register is done to get the final output.
I hope the above description makes the process less confusion instead of more.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi HRZ,
I appreciate the fast reply. Apologies for my late response.
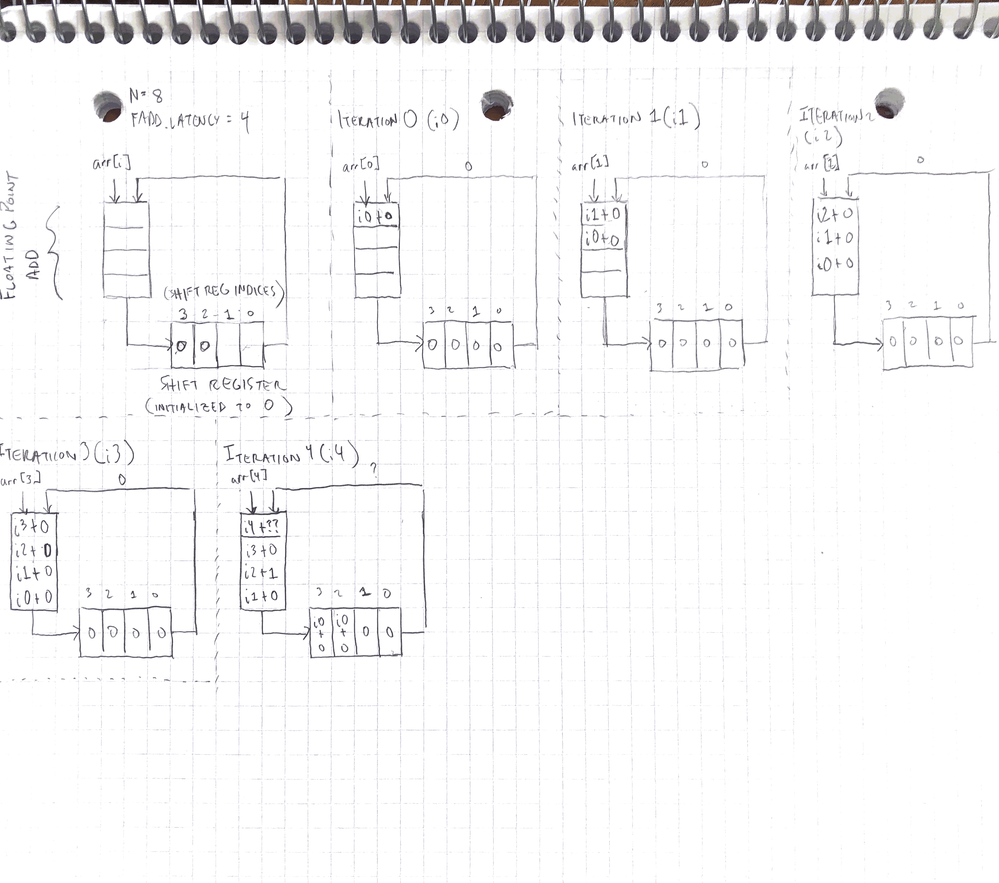
Your post is somewhat helpful, but I'm still confused as to what is actually happening at the hardware level. I've uploaded a picture of what I believe to be happening.
In the top left figure is my mental model of the hardware that is to be synthesized. (I am using a floating point add circuit that I'm assuming has a latency of 4 cycles instead of a double precision add with a latency of 11 cycles). The floating point add takes input from the array arr and from the shift register at position 0 (sr[0]). When the floating point add completes, it writes to the top of the shift register at position sr[3]. The total number of elements, N, to be accumulated is equal to 8, but I think I'm able to express my concern drawing up to iteration 4. Each panel shows what I believe the state of the accumulator circuit's pipeline (floating point add circuit and shift register) when an iteration is issued. When we get to iteration 4 (i4), based on what the C code as well as your well detailed response suggests, the shift register should be able to provide the result of i0 in order to add that to i4, but the value of i0 has not made it to position sr[0] yet. I think I'm missing something about what hardware is actually being synthesized, but I'm not sure what that thing is. Any further help would be appreciated.
Thanks!
A
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi @ACabr4,
Thank you for posting in Intel community forum, hope this message find you well and apologies for the delayed in response.
The explanation that are provided by HRZ are spot on as per my understanding too.
As for the details diagram, as for the iteration 1(i1) itself the shift register sr[3] should be already containing the result from i0, hence with the reach of i4 with the cycle mentioning to be 8, it will be a process is repeated at the register level.
Hope that clarify your doubts.
Warm regards.
BB
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi @ACabr4,
Hope this message find you well and good day, unfortunately as we do not receive any response from you to the previous clarification that we have provided. Please post a response in the next 15 days to allow me to continue to support you. After 15 days, this thread will be transitioned to community support. The community users will be able to help you with your follow-up questions.
Thank you
Warm Regards
BB
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page