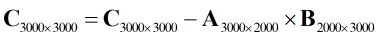Speedup of calculation for symmetric matrix using OMP

[nvh10]

My matrix calculation is: 

Here C is a symmetric matrix so I want to speed up this calculation by considering just the upper triangular and then take the opposite elelement. I used OMP and see that my implementation is slower than the normal calculation for the entire matrix C.

I also see that the calculation for C=C-AxB is slower than C=C+AxB.

My program is attached. Please advise me!

    Program testspeed
    implicit none
    integer nstate,nmeas,i,j,l
    integer(kind=8) :: tclock1, tclock2, clock_rate
    real(kind=8) :: elapsed_time
    double precision, allocatable, dimension(:,:):: B,C,A
    nstate =20000
    nmeas=10000
    allocate (B(nmeas,nstate),C(nstate,nstate),A(nstate,nmeas))
    A=1d0
    B=1d0
    call system_clock(tclock1)
    write(*,*) "1"
    !$omp parallel do
    do j = 1, nstate
        do l = 1,nmeas
            do i = 1, j
                C(j,i) = C(j,i) - A(j,l)*B(l,i)
                C(i,j)=C(j,i)
            end do
        end do
    end do
    !$omp end parallel do
    write(*,*) "2"
    call system_clock(tclock2, clock_rate)
    elapsed_time = float(tclock2 - tclock1) / float(clock_rate)
    write(*,*) elapsed_time
    end Program testspeed

[andrew_4619]

The inner most loop "i" is varying the second index of 2D arrays. That is intrinsically slow. It is more usual in Fortran to format arrays and loops so that the first index varies the most rapidly so that you are working with sequential memory locations. That way the loop are more likely to vectorise to allow multiple operations from in instructions and you are also jumping around memory much less. 

[nvh10]

Thanks for your comment. 

Is there any way I can improve the performance of my idea?

[nvh10]

Thanks for your comment. 

Is there any way I can improve the performance of my idea?

[jimdempseyatthecove]

As stated by Andrew_4619, have the inner most loop control variable (array index) be the left most index of the array.

Either change the order of the DO loops or order of the indexing, AND do the pivot in a separate loop:

    $omp parallel ! parallel region WITHOUT DO
    $OMP DO ! now start the DO in parallel
    do j = 1, nstate
        do l = 1,nmeas
            do i = 1, j
                C(i,j) = C(i,j) - A(l,j)*B(i,l)
            end do
        end do
    end do ! implicitly $omp end do, but not end end parallel
    !$omp do
    do i = 1, nstate
        do j = 2, i ! start at 2 (don't swap (1,1) with (1,1), (2,2) with (2,2), ...
            c(j,i) = c(i,j) ! writes with left most index varying most
        end do
    end do
    !omp end parallel
          

*** note the removal of: c(i,j) = c(j,i) *** which after swapping j and i

Do this on a separate pass in a manner such that the writes are performed sequentially.

Doing at the same time causes writes to be strided.

*** untested code above. It if left for you to take the guidance of changing your writes to be in sequential order.

Jim Dempsey

[andrew_4619]

As an aside I had a quick play with your code.  The line "C(i,j) = C(j,i)" seem so have a bit over 50 % of the time, i.e. removing that line more than halves the time taken.

It looks like you are  working on a tringle array and then making it symmetric. Is the outcome the same if you do the sym as a separate set of loop at the end because that is a double nested loop not a three way nested loop, it seem you are making some unnecessary operations (like x10000). 

[andrew_4619]

But noting the formula in your title if we code "c = c  - matmul(A,B)" that ran about x25 faster than your loops on my system.....